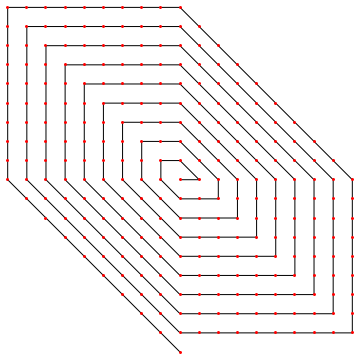
Алгоритм создания клеток по спирали на шестиугольном поле
Помогите найти алгоритм создания клеток по спирали на шестиугольном поле.
Посмотрите на изображение:
http://img685.imageshack.us/img685/927/fieldr.png
Давайте представим безразмерный 2d массив. Ось X - синяя линия, Y - горизонтальная, спираль - красная.
Мне нужно добавить клетки из центральной точки x0y0 в точку N по спирали
Подскажите, пожалуйста, способ решения проблемы. Спасибо!
6 ответов
Я бы посоветовал изменить нумерацию ячеек так, чтобы X оставалось неизменным, когда вы идете вниз и вправо (или вверх и влево). Тогда должен работать простой алгоритм, подобный следующему:
int x=0, y=0;
add(x, y); // add the first cell
int N=1
for( int N=1; <some condition>; ++N ) {
for(int i=0; i<N; ++i) add(++x, y); // move right
for(int i=0; i<N-1; ++i) add(x, ++y); // move down right. Note N-1
for(int i=0; i<N; ++i) add(--x, ++y); // move down left
for(int i=0; i<N; ++i) add(--x, y); // move left
for(int i=0; i<N; ++i) add(x, --y); // move up left
for(int i=0; i<N; ++i) add(++x, --y); // move up right
}
Это создает точки следующим образом:
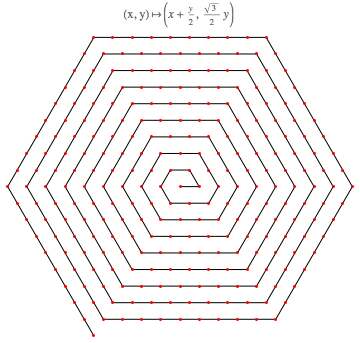
После преобразования получаем:
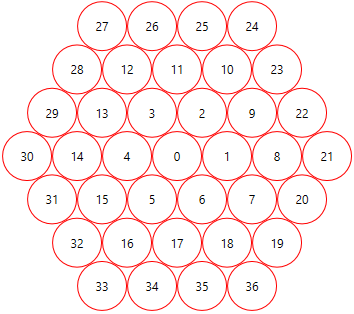
Вот функция, чтобы получить позицию i:
void getHexPosition( int i, ref double x, ref double y )
{
if ( i == 0 ) { x = y = 0; return; }
int layer = (int) Math.Round( Math.Sqrt( i/3.0 ) );
int firstIdxInLayer = 3*layer*(layer-1) + 1;
int side = (i - firstIdxInLayer) / layer; // note: this is integer division
int idx = (i - firstIdxInLayer) % layer;
x = layer * Math.Cos( (side - 1) * Math.PI/3 ) + (idx + 1) * Math.Cos( (side + 1) * Math.PI/3 );
y = -layer * Math.Sin( (side - 1) * Math.PI/3 ) - (idx + 1) * Math.Sin( (side + 1) * Math.PI/3 );
}
Масштабирование результата по Math.Sqrt(.75) дает
Если вы заинтересованы в перекосе координат, как в ответе Шуры:
int[] h = { 1, 1, 0, -1, -1, 0, 1, 1, 0 };
void getHexSkewedPosition( int i, ref int hx, ref int hy )
{
if ( i == 0 ) { hx = hy = 0; return; }
int layer = (int) Math.Round( Math.Sqrt( i/3.0 ) );
int firstIdxInLayer = 3*layer*(layer-1) + 1;
int side = (i - firstIdxInLayer) / layer;
int idx = (i - firstIdxInLayer) % layer;
hx = layer*h[side+0] + (idx+1) * h[side+2];
hy = layer*h[side+1] + (idx+1) * h[side+3];
}
void getHexPosition( int i, ref double hx, ref double hy )
{
int x = 0, y = 0;
getHexSkewedPosition( i, ref x, ref y );
hx = x - y * .5;
hy = y * Math.Sqrt( .75 );
}
Вы можете выбирать гексы по одному, используя соответствующую функцию счета, чтобы выбрать лучшее из шести еще не выбранных соседних гексов с гексом, выбранным в предыдущем раунде. Я думаю, что функция оценки, которая работает, состоит в том, чтобы выбрать самое близкое к (0,0) (заставляет выбирать гексы в одной "оболочке" за раз), разрывая связи, выбирая самое близкое к (1,0) (заставляет последовательное направление спирали в новой оболочке). Расстояние в шестнадцатеричной сетке можно вычислить с помощью следующей функции:
double grid_distance(int dx, int dy) {
double real_dx = dx + y/2.0;
double real_dy = dy * sqrt(3)/2.0;
return sqrt(real_dx * real_dx + real_dy * real_dy);
}
Представьте, что у вас есть нормальная сетка с квадратами вместо шестиугольников, создайте спираль, используя эту сетку, затем нарисуйте ее, сдвинув, скажем, каждый нечетный y влево на m пикселей, что даст вам этот эффект.
Ну, у меня была та же самая проблема, и предложения здесь не решили проблему, поскольку было заявлено, что я решил добавить свое решение...
private void generateMap(int size) {
// size is number of rings not counting center so array length is...
mapHexs = new Hex[(size*2)+1,(size*2)+1];
// offsets to traverse (sw,w,nw,ne,e,se) from a tile
int[,] offsetsOdd = new int[,] {{-1,-1},{-1,0},{-1,1},{0,1},{1,0},{0,-1}};
int[,] offsetsEven = new int[,] {{0,-1},{-1,0},{0,1},{1,1},{1,0},{1,-1}};
//start in the center
int posX = size;
int posY = size;
// each ring
for (int ring = 1; ring <= size; ring++) {
// at the start of a ring step out one
posX++;
// each side
for(int side = 0; side < 6; side++) {
// tiles per side
for(int idx = 0; idx < ring; idx++) {
// odd or even line
if(posY % 2 == 0) {
posX += offsetsEven[side,0];
posY += offsetsEven[side,1];
} else {
posX += offsetsOdd[side,0];
posY += offsetsOdd[side,1];
}
mapHexs[posX,posY] = new Hex();
}
}
}
}
Мне понравился подход @shura к этой проблеме, но я не смог заставить этот точный алгоритм работать. Кроме того, я использую шестигранный интервал 2x1 (где x ячеек разнесены на 2, а каждый другой x элемент скрыт).
Вот что я получил (хотя в JavaScript):
//Hexagon spiral algorithm, modified from
for(var n=1; n<=rings; ++n) {
x+=2; add(x, y);
for(var i=0; i<n-1; ++i) add(++x,++y); // move down right. Note N-1
for(var i=0; i<n; ++i) add(--x,++y); // move down left
for(var i=0; i<n; ++i) { x-=2; add(x, y); } // move left
for(var i=0; i<n; ++i) add(--x,--y); // move up left
for(var i=0; i<n; ++i) add(++x, --y); // move up right
for(var i=0; i<n; ++i) { x+=2; add(x, y); } // move right
}
Вы могли бы сделать это, имитируя направления. Если ваши направления "0 пунктов вверх", то увеличивайте их на 1 по часовой стрелке, выполните следующее:
Выберите центр ячейки.
Выберите вторую ячейку (в идеале в направлении 0).
Установите направление на 2.
Пока у вас есть больше клеток для отметки:
если ячейка в (направление +1)%6 свободна:
установить направление = (направление +1)%6
отметить текущую ячейку как использованную
идти к камере в направлении