Вывести вектор нормали многообразия из координат поверхности

Question

Уважаемые коллеги, пользователи stackru,

Я вычислительный химик и у меня проблемы с геометрией. У меня есть набор координат, которые определяют молекулярную поверхность, и я хотел бы вывести внешние нормальные векторы этой поверхности. Кажется, что поверхность аппроксимирует свойства многообразия, когда я на него смотрю, хотя координатные точки не были получены с использованием этого каркаса явно. Я должен также прояснить, что в общем случае молекулярные поверхности не всегда имеют выпуклую оболочку и могут иметь некоторую степень вогнутости. Чего у них нет, так это разрывов, поверхности по конструкции гладкие. Но так как я не знаю, что делать с этими математическими спецификациями, я попытался разработать алгоритм для общей проблемы.

В качестве предварительного замечания для каждой точки поверхности я могу определить положение ближайшего атома. Таким образом, для каждой точки у меня также есть эти координаты XYZ. Алгоритм принимает следующую форму:

1. Вычисление матрицы расстояний между каждой из доступных точек (которая неизбежно масштабируется до квадрата числа точек, но для моих случаев это целесообразно с использованием numpy)

2. Извлечение двух ближайших соседей каждой точки

3. Используйте эту тройку точек, чтобы сгенерировать два вектора с центром в каждой точке

4. Получите вектор нормали на основе перекрестного произведения этих двух векторов с последующей его нормализацией.

5. Рассчитать вектор между точкой и лежащим в ее основе атомом.

6. Если этот вектор составляет угол ниже 90° с вектором нормали, этот вектор направлен внутрь и, таким образом, заменяется его противоположным

Результат этой полной процедуры несколько нормален, но все же существуют различные векторы, которые, когда я визуально проверяю результат с помощью matplotlib, несколько параллельны поверхности. Вот результат matplotlib для молекулы воды: Вот молекулярная поверхность воды для сравнения (где вы можете найти основные атомы). Не обращайте внимания на цветовое кодирование поверхности, оно кодируется цветом поверхностным зарядом, что не имеет значения для настоящего обсуждения.

Эта поверхность получена сторонним программным обеспечением, из которого у меня нет доступа к коду. Я могу только визуализировать его и не могу получить доступ к процедурам сглаживания, используемым в нем для окончательного рендеринга.

Как видно из изображения, поверхность очень гладкая, и поэтому я ожидаю, что нормальные векторы будут объяснять эту "гладкость", что они делают несовершенно. Мне нужно, чтобы нормальные векторы действительно отражали гладкость поверхности, потому что шероховатость поверхности, изображенная настоящими нормальными векторами, оказывает заметное влияние на качество моих последующих вычислений на основе этих нормальных векторов. Кто-нибудь имеет представление о том, что я мог бы сделать, в течение разумного вычислительного времени, чтобы решить эту проблему?

Вот рабочий код, который будет воспроизводить мою первую фигуру:

import math
import matplotlib.pyplot      as plt
import numpy                  as np
from mpl_toolkits.mplot3d     import Axes3D
from sklearn.metrics.pairwise import euclidean_distances


coord = np.array([[ -1.2873729481345813 , 0.03256614731449952 , 1.5416924157851974 ],
[ 0.01652948394293976 , 1.163819319621563 , 1.6678642152662158 ],
[ 0.2794741299695759 , -0.5617278297487918 , 2.0029980474538105 ],
[ -0.6610946883884103 , -1.520269012229838 , 0.8599487353786675 ],
[ -1.0054760643749452 , 1.3940480132966795 , 0.33773540172063504 ],
[ 1.4883666878869983 , 0.43621600821755363 , 1.1450836953714032 ],
[ 1.093267571959524 , -1.3195317617899807 , 0.5499808804367919 ],
[ -0.044527698166979345 , -1.2654977063529413 , -0.7625313980846089 ],
[ 0.5831126343857715 , 1.5608391229347571 , -0.025329599172539626 ],
[ -1.0148260960520252 , 0.5209590347086124 , 1.6888058951547953 ],
[ -0.5081521680198725 , 0.9028613364971467 , 1.774471036317154 ],
[ -0.8515308971351676 , -0.19088994302497722 , 1.8836904989342724 ],
[ -0.28882376105739577 , -0.3548423909103548 , 2.05954224229103 ],
[ -1.2492850863979417 , -0.6364567978568106 , 1.3978142132864995 ],
[ -1.041946944653105 , -1.1796586713507826 , 1.095177216946184 ],
[ -1.5436272899575374 , -0.22919366151705667 , 1.1247655324014234 ],
[ -1.4689928122303186 , 0.5000569131417527 , 1.143407587573163 ],
[ -1.290329873679581 , 1.0646014214476844 , 0.8016157211074683 ],
[ 0.14732873180147785 , 0.6686847769257502 , 1.979342311827131 ],
[ 0.2131468214849169 , 0.056951984120299164 , 2.1073021163341092 ],
[ -0.0337308931325195 , -0.9942670995597854 , 1.8046165534409335 ],
[ -0.39947905888129415 , -1.37104542496434 , 1.3601926538530802 ],
[ -1.0634807007597644 , -1.3502061551644402 , 0.46773962277667314 ],
[ -0.7567553825092089 , 1.504835877060738 , 0.749651591341389 ],
[ -0.4472405474525535 , 1.4079282750475794 , 1.2824860152857014 ],
[ 1.5587883382335772 , -0.17395630632391745 , 1.1074452857884236 ],
[ 1.4235308457149791 , -0.8271279096055679 , 0.8993584919303867 ],
[ 0.7692195046037488 , -1.5167605398337778 , 0.1442407045573779 ],
[ 0.32445030395311525 , -1.4651179890494386 , -0.4390957189920336 ],
[ 0.00020957327211999695 , -0.9406835964416262 , -1.0384819480983047 ],
[ -0.025419507383719626 , 1.1326596798290633 , -0.892662493220727 ],
[ 0.273179306851356 , 1.4187473807855993 , -0.5317469722738123 ],
[ 1.0466981946916247 , 1.36444283710828 , 0.43534667343027367 ],
[ 1.3436060983763205 , 0.9793761802108056 , 0.8419277824771877 ],
[ 0.6151824124478109 , 0.9956899926113054 , 1.6618898508556756 ],
[ 1.1365292964079234 , 0.8011459463250883 , 1.4138732980146593 ],
[ 1.2547802693224217 , 0.08060290685487881 , 1.575156048146257 ],
[ 0.8061825016438882 , -0.24826596542943638 , 1.9004575307208522 ],
[ 0.7233645669036894 , -0.8826763855961071 , 1.6883835169082952 ],
[ 0.9497767017034661 , -1.2104420562255824 , 1.1703947277344628 ],
[ 0.5485586943697519 , -1.5967100787262565 , 0.7302017476622693 ],
[ -0.057205092501839166 , -1.6791781005999753 , 0.7696455114375087 ],
[ -0.48640523757119286 , -1.644761057333236 , 0.272618697792796 ],
[ -0.25748236328111623 , -1.501405645515218 , -0.39720000180351417 ],
[ -0.548591180200772 , 1.5966973503597166 , 0.07283122808381894 ],
[ 0.03137820171609954 , 1.6808890342631952 , 0.03811707406017944 ],
[ 0.5162256751875325 , 1.631621931751996 , 0.5739653241581716 ],
[ 0.29520943803145566 , 1.496670085663698 , 1.1960154986767626 ],
[ -0.4357510193390936 , 0.3045200764909755 , 2.0372933983710304 ],
[ -0.7252024085145093 , -0.8680072662231473 , 1.697293877794835 ],
[ -1.4026930025843594 , -0.8680775688445073 , 0.8886609086751069 ],
[ -1.0256665134561849 , 1.0589029487344046 , 1.2875897568848411 ],
[ 0.7343131121864293 , 0.4025541238612941 , 1.9038880538445522 ],
[ 0.2960177800611157 , -1.4085266358073394 , 1.3432377515245404 ],
[ -0.612740309720231 , -1.5270987389589377 , -0.09945502108597855 ],
[ -0.1766515084369774 , 1.6876887908829954 , 0.68242908228023 ],
[ 1.2576856987740817 , -0.6008401432185712 , 1.4092999027282396 ],
[ 0.20077831851211708 , -1.6825464196730353 , 0.10625820785053844 ],
[ -0.27284992140625597 , 1.4578679023663585 , -0.46947226287431315 ],
[ 0.9025274704849868 , 1.2861804462963813 , 1.101223178352364 ],
[ 1.7839350486036138 , -0.019389958495239716 , -1.0076276425199053 ],
[ 1.7377417775538346 , -0.8515596284340875 , -0.06551032812067904 ],
[ 1.9308978238593717 , 0.4526510335304934 , 0.15333098082293778 ],
[ 1.2640412923943216 , 1.1135989051613437 , -0.6487291165436305 ],
[ 0.7110361800083296 , 0.3011211057247756 , -1.4642623430903987 ],
[ 0.9695876990906258 , -0.9216814194628465 , -1.0943999970506841 ],
[ 2.04200929018949 , -0.17973742001943738 , -0.3635312878501747 ],
[ 1.8622593656466528 , 0.5635148250993117 , -0.6107377370213111 ],
[ 1.3955962627400398 , 0.5519618371910718 , -1.1944706185224625 ],
[ 1.2607629333920816 , -0.21551781723753682 , -1.3829616822422597 ],
[ 1.6583970787010358 , -0.6949731322511498 , -0.8399375243260477 ],
[ 1.9444143764920114 , -0.2454332569517364 , 0.2874392721860158 ],
[ 1.636157003293636 , 0.961650115510226 , -0.12326332301091819 ],
[ 0.8313542025004879 , 0.894165587734687 , -1.1420580452198033 ],
[ 0.6430205539552906 , -0.46024492898875324 , -1.4104511496936394 ],
[ 1.2947193164727608 , -1.1400972481068032 , -0.5315305572334722 ],
[ -1.7839430005914738 , 0.019376416779039715 , -1.0076136023161453 ],
[ -1.7377420093346745 , 0.8515508599214876 , -0.06550088225767904 ],
[ -1.9308962617200118 , -0.45265869341099335 , 0.15334861627561777 ],
[ -1.2640463026705615 , -1.1136106280858835 , -0.6487135972817705 ],
[ -0.7110478738279696 , -0.3011369604867556 , -1.4642554706297384 ],
[ -0.9695963617672257 , 0.9216674385272464 , -1.0943972008635638 ],
[ -2.04201196413603 , 0.17972714175629736 , -0.36351594480525473 ],
[ -1.8622640647650528 , -0.5635263554023318 , -0.6107201020978111 ],
[ -1.3956057456456397 , -0.5519763250811119 , -1.1944568661926225 ],
[ -1.2607739609741015 , 0.21550237470677686 , -1.3829529227257198 ],
[ -1.6584036564084357 , 0.6949604403980297 , -0.8399279355844478 ],
[ -1.9444117157749716 , 0.24542627653835639 , 0.2874534822565558 ],
[ -1.636157708161396 , -0.961659176659366 , -0.12324552404161819 ],
[ -0.8313632557119278 , -0.8941798105055468 , -1.1420471832711232 ],
[ -0.6430318069679907 , 0.46022934675447325 , -1.4104486921817194 ],
[ -1.294723366816481 , 1.1400861183930433 , -0.5315262031404322 ],
[ -4.5154929399999335e-06 , -0.6700687207417302 , -1.1844736267236027 ],
[ 0.16109703335223763 , -0.6271001397877708 , -1.2186543868869022 ],
[ -0.16110646810245766 , -0.6271000117262108 , -1.2186531586601221 ],
[ -4.0048342399999414e-06 , 0.6700542836529702 , -1.1844770214133027 ],
[ 0.16109751120177762 , 0.6270854068873908 , -1.218657563554442 ],
[ -0.16110599025291766 , 0.6270855243653509 , -1.2186563353276623 ],
[ 0.36994498278851456 , 0.7707305304675487 , -1.169504657558063 ],
[ 0.7025740208231097 , 1.1378228594549835 , -0.7470950439135691 ],
[ 1.1902461772283626 , 1.1877239069058625 , -0.12779283816255813 ],
[ 1.5961784560313765 , 0.748033999209189 , 0.38770812025235435 ],
[ 1.7530425415210142 , -3.3999814999999503e-06 , 0.5869144868197315 ],
[ 1.5961778861045166 , -0.748041688194589 , 0.3877119097103343 ],
[ 1.1902452718013825 , -1.1877338978242624 , -0.12778682138595815 ],
[ 0.7025731540262697 , -1.1378356163972434 , -0.7470892795558292 ],
[ 0.3699443953987146 , -0.7707451739365088 , -1.1695007532680228 ],
[ 0.27881228877701597 , 1.0004381797559854 , -0.9277686907765464 ],
[ 0.7663313983885688 , 1.3243776625508408 , -0.3086616683059155 ],
[ 1.2752305145620413 , 1.102396662519724 , 0.337597800103595 ],
[ 1.5957376215740167 , 0.42599740483075377 , 0.7446167357487491 ],
[ 1.5957372971866766 , -0.4260032850789138 , 0.7446188937447891 ],
[ 1.2752296742242015 , -1.102404360501184 , 0.3376033845401351 ],
[ 0.7663303887131288 , -1.3243882472092006 , -0.3086549593618755 ],
[ 0.27881152675781595 , -1.0004515288506655 , -0.9277636228196864 ],
[ -0.36995352216617455 , -0.7707449252219087 , -1.169497906808803 ],
[ -0.7025791448730497 , -1.1378352248040433 , -0.747083649080629 ],
[ -1.1902463164027026 , -1.1877331892522427 , -0.12777707971133812 ],
[ -1.5961744570181167 , -0.748040609725749 , 0.3877250868215143 ],
[ -1.7530369449133343 , -2.0638019999999696e-06 , 0.5869289937602514 ],
[ -1.5961738870912567 , 0.748035353909989 , 0.38772129736353433 ],
[ -1.1902454109757226 , 1.1877250123628826 , -0.12778309701711812 ],
[ -0.7025782780762097 , 1.1378235389221032 , -0.747089413438369 ],
[ -0.3699529347763746 , 0.7707308453296488 , -1.1695018110988429 ],
[ -0.27881865163733593 , -1.0004514007891054 , -0.9277613558125664 ],
[ -0.7663327657896889 , -1.3243878630245205 , -0.3086485986182755 ],
[ -1.2752266880614613 , -1.102403584723304 , 0.33761404540041506 ],
[ -1.5957305300328366 , -0.42600214945863374 , 0.7446322698276491 ],
[ -1.5957302056454967 , 0.42599870132175377 , 0.7446301118316091 ],
[ -1.2752258482528014 , 1.102397829890804 , 0.33760846043469506 ],
[ -0.7663317561142488 , 1.3243784467956008 , -0.3086553075623155 ],
[ -0.2788178890889559 , 1.0004384766259653 , -0.9277664242986065 ],
[ -0.23018790924333662 , 0.4635384934491132 , -1.3322307085678806 ],
[ -0.23018827914015663 , -0.20734291124417695 , -1.3622983801385802 ],
[ 0.23017815010577664 , 0.20732757296187695 , -1.3623011720922602 ],
[ 0.23017800828553664 , -0.46355367932757324 , -1.3322301015984204 ]])

atoms = np.asarray([[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -1.21073950301e-06 , 0.0 , 0.40150605663 ],
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ -0.764815694412 , 0.0 , -0.200752550787 ], 
[ 0.764816906209 , 0.0 , -0.200753505843 ],  
[ 0.764816906209 , 0.0 , -0.200753505843 ]])

#transpose coordinate array
xyz = np.transpose(coord)

#establish distance matrix
n = len(coord)
dist_vectors    = list()
dist_vectors.append(xyz[0])
dist_vectors.append(xyz[1])
dist_vectors.append(xyz[2])
dist_vectors    = map(list, zip(*dist_vectors))
d               = euclidean_distances(dist_vectors, dist_vectors)

#find two nearest neighbors for each segment
x1 = np.zeros((n))
x2 = np.zeros((n))
y1 = np.zeros((n))
y2 = np.zeros((n))
z1 = np.zeros((n))
z2 = np.zeros((n))

for i in range(n):
    x_copy = xyz[0]
    y_copy = xyz[1]
    z_copy = xyz[2]

    d1     = np.delete(d[i], i) #removes distance between segment and itself
    x_copy = np.delete(x_copy, i)
    y_copy = np.delete(y_copy, i)
    z_copy = np.delete(z_copy, i)
    j1     = np.argmin(d1)      #get indice of minimum distance
    x1[i]  = x_copy[j1]
    y1[i]  = y_copy[j1]
    z1[i]  = z_copy[j1]
    d2     = np.delete(d1, j1)  #removes minimum distance
    x_copy = np.delete(x_copy, j1)
    y_copy = np.delete(y_copy, j1)
    z_copy = np.delete(z_copy, j1)
    j2     = np.argmin(d2)      #get indice of second minimum distance
    x2[i]  = x_copy[j2]
    y2[i]  = y_copy[j2]
    z2[i]  = z_copy[j2]

#compute normal vector for each segment based on cross product
normal    = list() 
forGraphs = list()
for i in range(n):
    #make vectors for cross product
    v1 = np.zeros((3))
    v1[0] = x1[i] - coord[i][0]
    v1[1] = y1[i] - coord[i][1]
    v1[2] = z1[i] - coord[i][2]
    v2 = np.zeros((3))
    v2[0] = x2[i] - coord[i][0]
    v2[1] = y2[i] - coord[i][1]
    v2[2] = z2[i] - coord[i][2]

    #make cross product and normalize (normal vector should have a unit norm)
    nv = np.cross(v1, v2)

    nv = nv / np.linalg.norm(nv)
    normal.append(nv)

    #check of outwards pointing
    atv    = np.zeros((3))
    atv[0] = atoms[i][0] - coord[i][0]
    atv[1] = atoms[i][1] - coord[i][1]
    atv[2] = atoms[i][2] - coord[i][2]

    th_check = math.acos(np.dot(nv, atv) / (np.linalg.norm(nv) * np.linalg.norm(atv)))
    if th_check < (math.pi / 2): #if inwards pointing (i. e. pointing towards underlying atom), normal vector is replaced by its opposite
        nv[0] = -nv[0]
        nv[1] = -nv[1]
        nv[2] = -nv[2]
    forGraphs.append(np.array([coord[i][0],coord[i][1],coord[i][2],nv[0],nv[1], nv[2]]))

#plot normal vectors (for checkup)
forGraphs = np.asarray(forGraphs)
X, Y, Z, U, V, W = zip(*forGraphs)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.quiver(X, Y, Z, U, V, W)
ax.set_xlim([min(xyz[0])- 1, max(xyz[0]) + 1])
ax.set_ylim([min(xyz[1])- 1, max(xyz[1]) + 1])
ax.set_zlim([min(xyz[2])- 1, max(xyz[2]) + 1])
plt.show()

Первые 280 строк этого кода в основном посвящены координатным таблицам, необходимым для воспроизведения результата. Самая важная часть этого кода - от строки 282 до строки 355, где реализован алгоритм, который я только что изложил.

Заранее спасибо за вашу помощь!

Answer 1

"Стандартная" процедура оценки нормалей для каждой точки состоит в том, чтобы найти k ближайших соседей, где k - небольшое число (десять?). Затем, чтобы вычислить лучшую плоскость, подходящую через эти точки, и использовать нормаль к плоскости.

К сожалению, возникает проблема, заключающаяся в том, что знак нормального значения не определен, и вам необходимо реализовать нормальный процесс обеспечения согласованности. Возможно, в вашем случае это проще, так как все нормали, кажется, указывают в сторону от некоторой центральной точки.

Answer 2

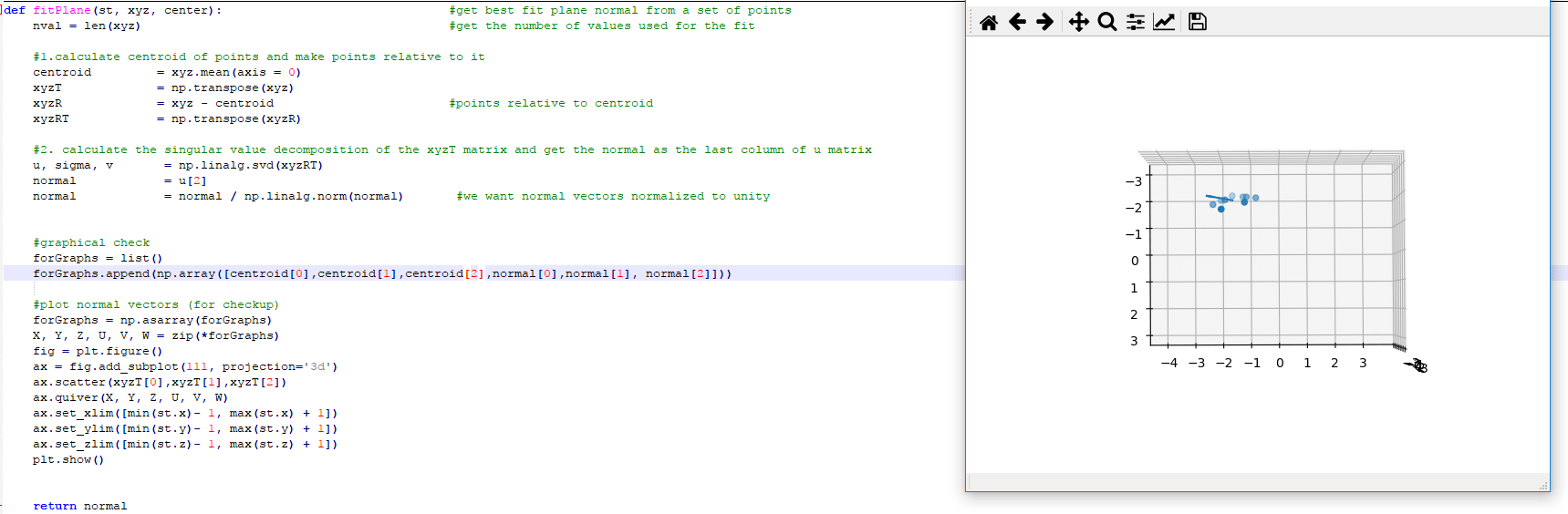
Я использовал технику ближайших соседей, следуя предложению @Yves Daoust, и подогнал плоскость через 10 ближайших соседей, используя разложение по сингулярным значениям (SVD). Это все еще дает неправильные ответы в визуально простых случаях. Я не понимаю почему. Вот пример того, что я получаю: