Подразделить многосегментный кубический безье сплайн

Question

Прежде всего позвольте мне извиниться за плохой английский и, возможно, не очень прямой вопрос, так как я не совсем уверен, как его назвать.

У меня есть много сегментированная кривая Кубического Безье в After Effects, она определяется 5 вершинами с касательными IN & OUT. Моя задача состоит в том, чтобы разделить его на N небольших линейных кусков в Java Script.

РЕДАКТИРОВАТЬ прислано больше информации. Учитывая многосегментный сплайн Кубического Безье, определяемый 5 точками с касательными In & Out, мне нужно получить его линейное представление. Где N - количество линейных сегментов, определенных пользователем.

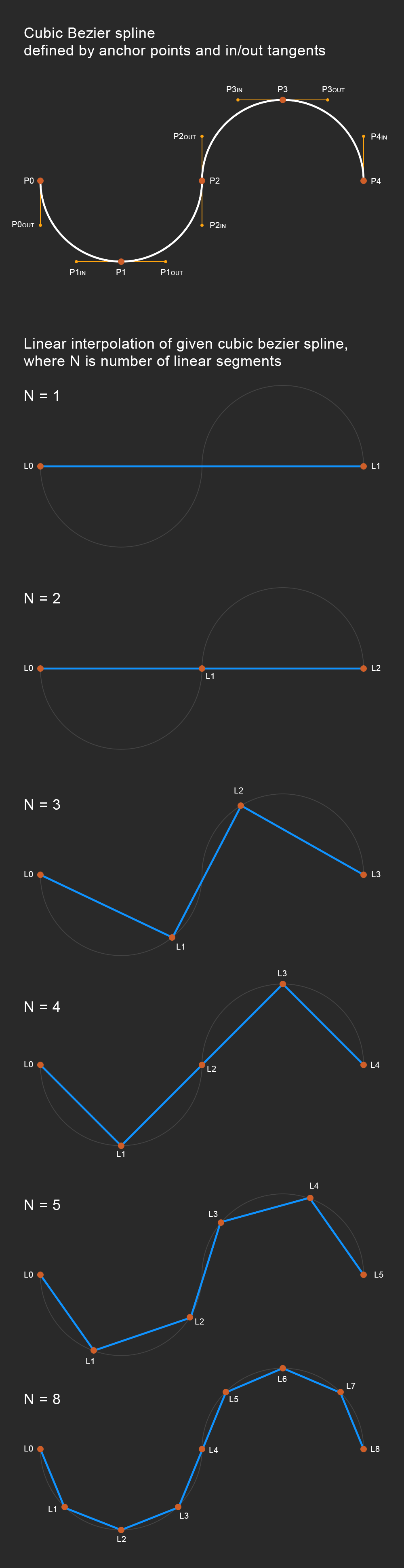
Кубический Безье Сплайн:

Segment1: P0, P0out, P1in, P1;
Segment2: P1, P1out, P2in, P2;
Segment3: P2, P2out, P3in, P3;
Segment4: P3, P3out, P4in, P4;

Ожидаемый результат:

N = 1: linear spline with 2 anchors representing entire shape;
N = 2: linear spline with 3 anchors representing entire shape;
N = 3: linear spline with 4 anchors representing entire shape;
N = 4: linear spline with 5 anchors representing entire shape;
...
N = 8: linear spline with 9 anchors representing entire shape;

distance(L0,L1) = distance(L1,L2) = distance(L2,L3) = ... = distance(L-n, Ln)

В примере изображения я использую 4-сегментный сплайн, где длина сегмента равна друг другу - это просто нарисовать, чтобы объяснить мою задачу. Но в реальном проекте эти сегменты не будут равны, и всего будет более 4 сегментов.

Я рассмотрел метод де Кастеляу, но, насколько я понимаю, он работает с одним сплайном сегмента. Мои математические навыки пыльные, поэтому я не совсем уверен, смогу ли я использовать де Кастельжау в своем примере.

Answer 1

Это концептуально просто, хотя может быть связано с небольшим количеством кода по причинам, объясненным чуть позже. Вы пытаетесь сгладить (кубический) поли-Безье, поэтому давайте начнем с этого:

Отдельные кубические кривые Безье создаются четырьмя точками: начальной точкой, контрольной точкой, определяющей касательную в начальной точке, конечной точкой и контрольной точкой, определяющей касательную в конечной точке. Таким образом, кривая представляет собой график кубической функции Безье:

Bx(t) = p1.x × (1-t)³ + 2 × p2.x × (1-t)² × t + 2 × p3.x × (1-t) × t² + p4.x × t³
By(t) = p1.y × (1-t)³ + 2 × p2.y × (1-t)² × t + 2 × p3.y × (1-t) × t² + p4.y × t³

Одна кривая Безье построена на интервале t=[0,1]Таким образом, поли-Безье из N сегментов строится на всем интервале N × [0,1],

Во-первых, простой случай: простое выравнивание. Кривые Безье - это нелинейные кривые, поэтому давайте сначала не будем приводить в исполнение "одинаковую длину для каждого из отрезков". Учитывая N-сегментный поли-Безье:

S = number of segments we want
points = empty list
for (s = 0):(s = S):(step = S/N):
  v = s * step
  segmentid = floor(v)
  segment = polycurve.segments[segmentid] 
  t = v % 1
  points.push(
    segment.pointAt(t)
  )

Теперь у нас есть все нужные нам точки, и мы просто соединяем их линиями. Готово.

Однако кривые Безье являются нелинейными кривыми, поэтому уплощение таким образом не дает равноотстоящих сегментов в малейшей степени. Если мы хотим сделать это, нам нужно работать с расстоянием вдоль кривой, а не t ценности.

S = number of segments we want
points = empty list
for (s = 0):(s = S):(step = S/N):
  v = s * step
  segmentid = floor(v)
  segment = polycurve.segments[segmentid]
  distanceRatio = v % 1
  t = segment.getTforDistanceRatio(distanceRatio)
  points.push(
    segment.pointAt(t)
  )

Это будет работать именно так, как вы хотите, но getTforDistanceRatio это сложная часть, потому что то, что мы здесь делаем, - это перепараметризация кривой для расстояния, а не для времени, и это очень сложная математическая задача (для которой не существует общего символического решения). Самый дешевый способ сделать это - использовать таблицу поиска (LUT), которая описана в ссылке выше, для "расстояния вдоль кривой".

Answer 2

Метод де Кастельжау используется для вычисления точки на кривой Безье, а также для получения контрольных точек для двух подразделенных кривых в процессе. Итак, да, вы должны иметь возможность использовать метод де Кателье, чтобы оценить столько точек, сколько вы хотите на кривой Безье, если вы знаете контрольные точки.

Из изображения, которое вы показываете, и того факта, что ваш "кубический сплайн Безье" принимает входные / выходные касательные в качестве входных данных, я думаю, что ваш сплайн на самом деле является "кубическим сплайном Эрмита", в котором каждый сегмент действительно является кубической кривой Безье. Вы можете преобразовать каждый сегмент вашего сплайна в кубическую кривую Безье, затем использовать метод де Кателье, чтобы оценить столько точек, сколько хотите, а затем соединить эти точки прямыми линиями.