Получение трассировки для сохранения значения в R

Я бегу nloptr пакет в R который представляет собой пакет для нелинейной оптимизации. В пределах nloptr пакет, который я использую cobyla() Команда для выполнения моей оптимизации. Теперь я могу указать максимальное количество итераций алгоритма, используя maxeval параметр, но когда cobyla() Команда выполняет это только позволяет мне увидеть вывод для окончательной оценки. Тем не менее, я хотел бы видеть все выходные данные на каждой итерации метода.

Кто-то порекомендовал мне использовать trace() Команда, чтобы иметь возможность видеть все промежуточные выходные данные, но я не могу понять, как получить R хранить эту информацию. Может кто-нибудь предложить мне, как сделать это с помощью trace() (или любым другим способом).

Вот код, с которым я работаю:

library(nloptr)


#########################################################################################
### 
#########################################################################################
f = function(x){
    ans = cos(pi*x/5)+.2*sin(4*pi*x/5)

    return(ans)
}

const = function(x){
    ans = numeric(1)
    ans[1] = -(sin(pi*x/5)+.2*cos(4*pi*x/5))
    return(ans)
}

#########################################################################################
###
#########################################################################################

x0 = runif(1,0,10)

COB = cobyla(x0,f,hin=const,lower=0,upper=10,nl.info = TRUE,
      control = list(xtol_rel = 1e-16, maxeval = 2000))

Поэтому я хотел бы иметь возможность хранить вывод для запуска cobyla() для итераций 1,2,...,maxeval

И вот что я думаю, что мне нужно сделать, это использовать

trace(f)

или же

trace(cobyla)

до выполнения кода, но я не уверен, как сохранить значения запуска trace() команда

Источник

2 ответа

Решение

Ваша лучшая ставка, без настройки nloptr код, чтобы установить print_level возможность 3отправить вывод на sink и очистить его, чтобы получить то, что вам нужно.

Обратите внимание, что использовать print_level Вы не можете использовать функцию оболочки cobyla - вместо этого вы должны перейти к nloptr функция.

Наконец, обратите внимание, что cobyla и nloptr функция с algorithm = NLOPT_LN_COBYLA, ведут себя по-разному - первый принимает ограничения неравенства для>= 0, а второй принимает их как <=0.

В приведенном ниже коде первым делом я использую ядро nloptr функции и показать, что это приводит к тому же ответу, что и использование cobyla код обёртки.

Затем я установил print_level = 3 и запишите это в файл. Когда оптимизация завершена, я прочитал этот файл и использую регулярные выражения для извлечения пути решения из вывода.

Вот как это выглядит: 

library(tidyr)
library(nloptr)
library(assertthat)
library(dplyr)
library(ggplot2)

# starting parameter values
x0.hs100 = c(1, 2, 0, 4, 0, 1, 1)

# objective function
fn.hs100 = function(x) {
  (x[1]-10)^2 + 5*(x[2]-12)^2 + x[3]^4 + 3*(x[4]-11)^2 + 10*x[5]^6 +
    7*x[6]^2 + x[7]^4 - 4*x[6]*x[7] - 10*x[6] - 8*x[7]
}

# inequality constraints
# NOTE: nloptr with algorithm = NLOPT_LN_COBYLA takes g(x) <= 0
hin.hs100 = function(x) {
  h = numeric(4)
  h[1] = 127 - 2*x[1]^2 - 3*x[2]^4 - x[3] - 4*x[4]^2 - 5*x[5]
  h[2] = 282 - 7*x[1] - 3*x[2] - 10*x[3]^2 - x[4] + x[5]
  h[3] = 196 - 23*x[1] - x[2]^2 - 6*x[6]^2 + 8*x[7]
  h[4] = -4*x[1]^2 - x[2]^2 + 3*x[1]*x[2] -2*x[3]^2 - 5*x[6]    +11*x[7]
  return(-h)
}

# compute the solution
sink(file = "Output/cobyla_trace.txt", type = "output")
S1 = nloptr(x0 = x0.hs100, 
            eval_f = fn.hs100,
            eval_g_ineq = hin.hs100,
            opts = list(algorithm = "NLOPT_LN_COBYLA", 
                        xtol_rel = 1e-8, maxeval = 2000, print_level = 3))
sink()

# inequality constraints
# NOTE: cobyla takes g(x) >= 0
hin.hs100_minus = function(x) {
  h = numeric(4)
  h[1] = 127 - 2*x[1]^2 - 3*x[2]^4 - x[3] - 4*x[4]^2 - 5*x[5]
  h[2] = 282 - 7*x[1] - 3*x[2] - 10*x[3]^2 - x[4] + x[5]
  h[3] = 196 - 23*x[1] - x[2]^2 - 6*x[6]^2 + 8*x[7]
  h[4] = -4*x[1]^2 - x[2]^2 + 3*x[1]*x[2] -2*x[3]^2 - 5*x[6]    +11*x[7]
  return(h)
}

# compute the solution
S2 = cobyla(x0.hs100, fn.hs100, hin = hin.hs100_minus,
            nl.info = TRUE, control = list(xtol_rel = 1e-8, maxeval = 2000))

# check that both return the same solution
assertthat::are_equal(S1$solution, S2$par)

# get the solutions from the output file
solutionPath = readLines(con = file("Output/cobyla_trace.txt"))

# extract the solution path data out of the raw output
solutionPathParamRaw = solutionPath[grepl("^\tx", solutionPath)]
solutionPathParamMatch = gregexpr("(-)?[0-9]+(\\.[0-9]+)?", solutionPathParamRaw, perl = TRUE)
solutionPathParam = as.data.frame(
  t(
    sapply(
      regmatches(
        solutionPathParamRaw, solutionPathParamMatch
      ), 
      as.numeric, simplify = TRUE
    )
  )
)

# give the columns some names
names(solutionPathParam) = paste("x", seq(1, 7), sep = "")
solutionPathParam$IterationNum = seq(1, dim(solutionPathParam)[1])

# plot the solutions
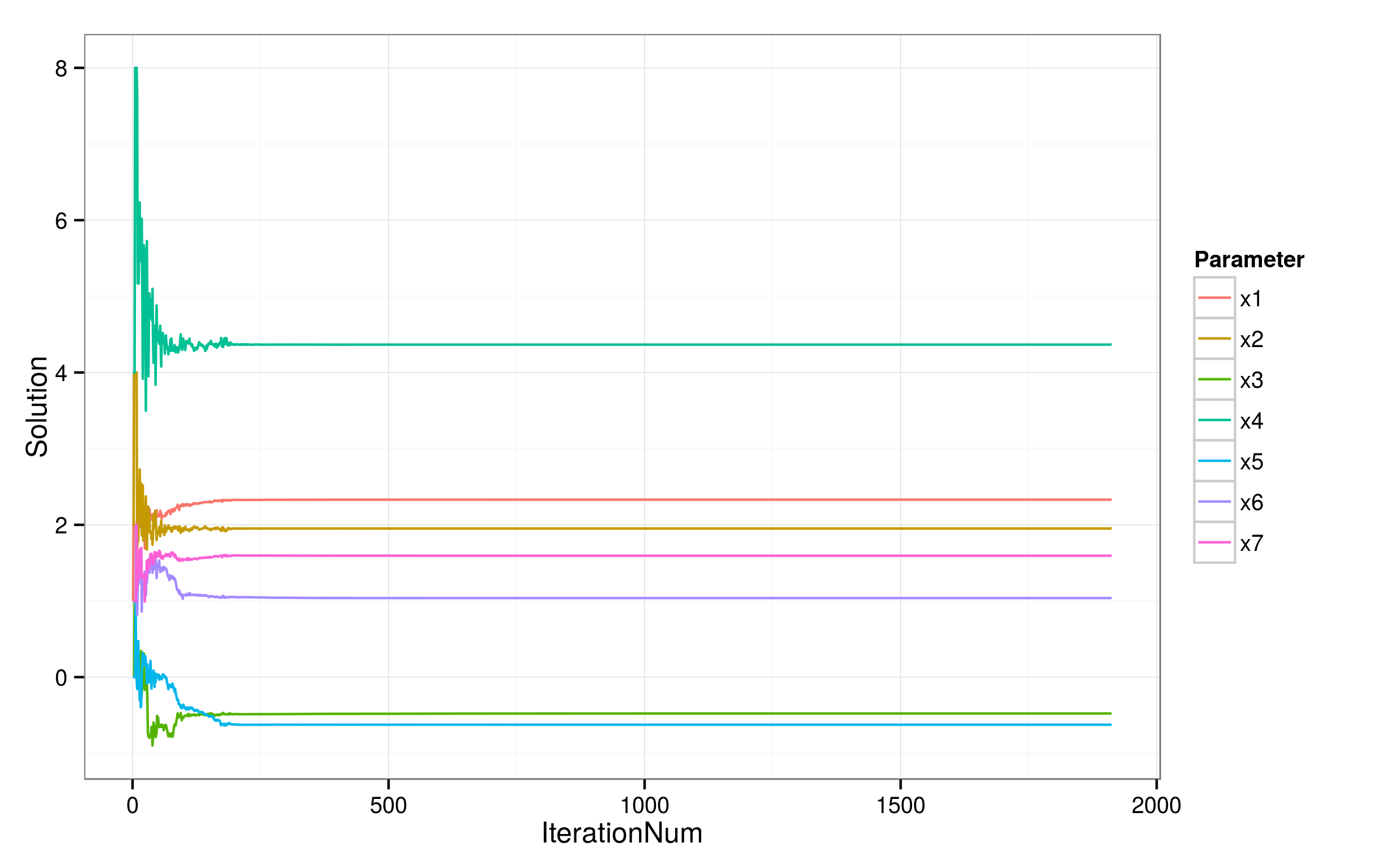
solutionPathParam %>%
  gather(Parameter, Solution, -IterationNum) %>%
  ggplot(aes(x = IterationNum, y = Solution, group = Parameter, color = Parameter)) +
  geom_line() + 
  theme_bw()

ggsave("Output/SolutionPath.png")
Источник

Если предположить, что Джош прав в своем комментарии, тогда вам нужно сделать цикл самостоятельно. Это будет выглядеть примерно так...

maxeval<-2000
x0<-c()
x0[1] = runif(1,0,10)
for (cureval in 1:maxeval) {
    COB = cobyla(x0[cureval],f,hin=const,lower=0,upper=10,nl.info = TRUE,
      control = list(xtol_rel = 1e-16, maxeval = 1))
    x0[cureval+1]  <-COB$par

  }
Источник
Другие вопросы по тегам