Использование JAGS для оценки среднего покрытия навеса с биномиальным и 20 образцами / участок
Я хотел бы оценить медианы, а также 5, 25, 75 и 95-й процентили покрытия навеса для 13 групп (записанных как количество точек из 20 с присутствием растительности или без) и всего 223 образца. Ранее я публиковал это, предполагая бета-дистрибутив, но это было неправильно. Это для рукописи, которая просрочена, и это последняя часть, которая отсутствует. Я был бы очень признателен, если бы кто-нибудь помог мне завершить (только до тех пор, пока код не заработает). Я думаю, что я близко, просто нужно немного подправить - я думаю.
(Я вошел, чтобы отредактировать, чтобы зафиксировать два отрицательных голоса, но я не уверен, что не ясно).
БОЛЬШОЕ БОЛЬШОЕ СПАСИБО!
Ниже мое модельное заявление, код R и данные. Я получаю ошибку:
model(model.file, data = data, inits = init.values, n.chains = n.chains, :
RUNTIME ERROR:
Compilation error on line 16.
Subset out of range: re[14]
Но обратите внимание, что я удалил пробелы ниже, и ошибка относится к утверждению вероятности.
model{
# priors
for (i in 1:13){
alpha[i] ~ dunif(0, 1)
re[i] ~ dnorm(0, 0.001)
}
#likelihood
for (i in 1:223) {
canopy[i] ~ dbin(p[i], 20)
logit(p[i]) <- alpha[site[i]] + re[i]
}
median <- 1/(1+exp(alpha[site[i]]))
t4est1_100 <- step(median[1]-median[4])
t5est1_10 <- step(median[3]-median[4])
t6est10_100 <- step(median[2]-median[3])
}
Код R:
cover <- read.csv("f:\\brazil\\canopy2.csv", header=T)
library(R2jags)
library(rjags)
setwd("f://brazil")
site <- frag$site
canopy <- frag$canopy*20
N <- length(frag$site)
jags.data <- list("site", "canopy")
jags.params <- c("median", "test100MF","test100MT","test100fc","test100fa",
"test100gv","test100hm","test100mc", "test100ca","test100ct", "test10MF",
"test10MT", "test10fc","test10fa", "test10gv", "test10hm", "test10mc", "test10ca",
"test10ct", "test1MF", "test1MT", "test1fc", "test1fa", "test1gv", "test1hm",
"test1mc", "test1ca", "test1ct", "t1est1_con","t2est10_con","t3est100_con",
"t4est1_100","t5est1_10","t6est10_100")
#inits1 <- list(a=0, sd=0)
#inits2 <- list(a=100, sd=50)
#jags.inits <- list(inits1, inits2)
jags.inits <- function() {
list(alpha = 0, re=0)}
jagsfit2 <- jags(data=jags.data, inits=jags.inits, jags.params,
n.iter=1000000, n.burnin=20000, model.file="fragmodelbinom.txt")
my.coda <- as.mcmc(jagsfit2)
summary(my.coda, quantiles=c(0.05, 0.25,0.5,0.75, 0.95))
print(jagsfit2, digits=3)
Данные:
structure(list(site = c(1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L,
1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L,
2L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L, 3L,
3L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L, 4L,
4L, 4L, 4L, 4L, 4L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L,
5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 5L, 6L, 6L, 6L, 6L,
6L, 6L, 6L, 6L, 6L, 6L, 6L, 6L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L,
7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 7L, 8L, 8L, 8L, 8L, 8L, 8L, 8L,
8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 8L, 9L, 9L, 9L, 9L, 10L, 10L,
10L, 11L, 11L, 11L, 11L, 11L, 11L, 11L, 11L, 12L, 12L, 12L, 12L,
13L, 13L, 13L, 13L, 13L, 13L, 13L, 13L, 13L, 13L, 13L, 13L, 13L
), canopy = c(0, 0.05, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6,
0.6, 0.6, 0.65, 0.65, 0.7, 0.7, 0.7, 0.7, 0.7, 0.7, 0.75, 0.75,
0.8, 0.8, 0.85, 0.85, 0.85, 0.85, 0.85, 0.85, 0.9, 0.9, 0.9,
0.9, 0.95, 0.95, 0.95, 0.95, 0.95, 1, 1, 1, 1, 1, 1, 0.05, 0.2,
0.25, 0.4, 0.4, 0.5, 0.6, 0.6, 0.65, 0.65, 0.75, 0.75, 0.75,
0.8, 0.8, 0.8, 0.8, 0.85, 0.85, 0.85, 0.9, 0.9, 0.95, 0.95, 0.95,
0.95, 1, 1, 1, 1, 1, 0, 0.2, 0.25, 0.3, 0.35, 0.4, 0.4, 0.45,
0.45, 0.5, 0.5, 0.55, 0.6, 0.7, 0.7, 0.7, 0.8, 0.85, 0.9, 0.9,
0.9, 0.95, 0.95, 0.95, 0.95, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0,
0.1, 0.4, 0.4, 0.45, 0.5, 0.55, 0.55, 0.7, 0.7, 0.75, 0.8, 0.8,
0.8, 0.9, 1, 1, 0.15, 0.2, 0.25, 0.25, 0.35, 0.5, 0.5, 0.55,
0.65, 0.7, 0.7, 0.75, 0.8, 0.85, 0.85, 0.9, 0.9, 0.95, 0.95,
1, 1, 1, 1, 0.05, 0.4, 0.6, 0.65, 0.65, 0.65, 0.7, 0.85, 0.95,
1, 1, 1, 0.35, 0.4, 0.4, 0.5, 0.5, 0.55, 0.65, 0.65, 0.75, 0.75,
0.8, 0.85, 0.9, 0.9, 1, 1, 1, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7,
0.8, 0.8, 0.8, 0.85, 0.95, 0.95, 1, 1, 1, 1, 0.8, 0.85, 1, 1,
1, 1, 1, 0, 0.05, 0.1, 0.15, 0.5, 0.6, 0.6, 0.75, 0.1, 0.35,
0.6, 1, 0.4, 0.5, 0.55, 0.65, 0.65, 0.8, 0.9, 0.9, 0.9, 0.9,
0.95, 0.95, 1)), .Names = c("site", "canopy"), class = "data.frame",
row.names = c(NA, -227L))
2 ответа
Я вижу две очевидные ошибки, читая ваш код. В определении модели у вас есть:
for (i in 1:223) {
canopy[i] ~ dbin(p[i], 20)
logit(p[i]) <- alpha[site[i]] + re[i]
}
Вышесказанное не может быть правильным, так как re Параметр имеет всего 13 компонентов, как вы его определили. Я думаю, это должно быть re[site[i]] вместо. Это является причиной ошибки, которую вы получаете.
Вторая линия median <- 1/(1+exp(alpha[site[i]])): он находится вне цикла for, хотя я думаю, что он должен быть внутри, так как это зависит от i,
В JAGS, dbin принимает вероятность успеха и количество попыток и возвращает целое число, указывающее количество успехов. В вашей модели вы указываете, что результаты dbin ваш canopy значения, которые лежат между 0 и 1 - это неверно.
Почему вы указываете 20 испытаний? Есть ли двадцать точек, в которых вы оценивали наличие / отсутствие вида? Если это так, возможно, вы должны указать свою модель данных как:
y[i] ~ dbin(cover[i], 20)
где y[i] является целым числом, указывающим количество присутствий вида на сайте i (это ваши данные), и cover это то, что мы пытаемся оценить, то есть пропорциональное покрытие видов, зарегистрированных в качестве наблюдения i). ( Fukaya et al. (2010) предоставляют код для аналогичной проблемы, где они оценивают вероятность появления ракушки на участках съемки - может быть стоит прочитать.)
Вот пример, использующий смоделированные данные, которые представляют вашу проблему (или, по крайней мере, мое понимание), которые будут компилироваться и для которых JAGS оценивает достаточно точные значения покрытия.
M <- function() {
for (j in 1:13){
alpha[j] ~ dnorm(0, 0.0001)
}
for (i in 1:length(y)) {
y[i] ~ dbin(p[i], 20)
logit(p[i]) <- alpha[site[i]] + eps[i]
eps[i] ~ dnorm(0, sd^-2)
}
sd ~ dunif(0, 100)
}
Обратите внимание, что я использовал туманный нормальный априор для alpha, а не ваша форма (0, 1) до, так как alpha находится в масштабе логита и поэтому не ограничен 0 и 1. Я переименовал re в eps для наглядности и перенес его в петлю уровня наблюдения.
site <- c(1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3,
3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4,
4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5,
5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7,
7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 8, 8,
8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 10, 10, 10, 11, 11, 11, 11,
11, 11, 11, 11, 12, 12, 12, 12, 13, 13, 13, 13, 13, 13, 13, 13,
13, 13, 13, 13, 13)
set.seed(1)
alpha <- rnorm(13) # 13 independent random site intercepts
sd <- 0.123 # a constant variance for obs around alphas
logit.p <- rnorm(length(site), alpha[site], sd) # logit probs
y <- sapply(plogis(logit.p), rbinom, n=1, size=20)
Несколько графиков, чтобы показать данные, которые мы смоделировали:
plot(plogis(logit.p) ~ site, pch=20, las=1, ylab='p', ylim=c(0, 1))
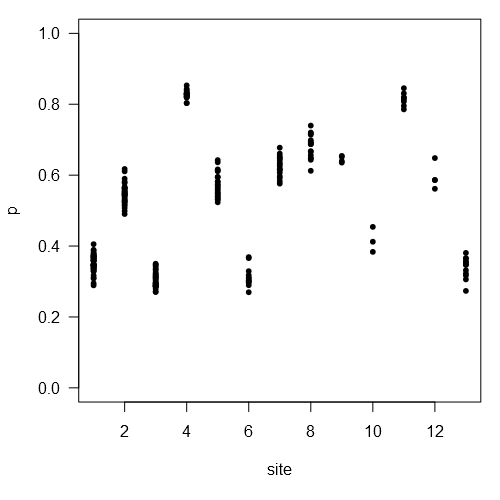
plot(y ~ jitter(site), pch=20, las=1, xlab='site')
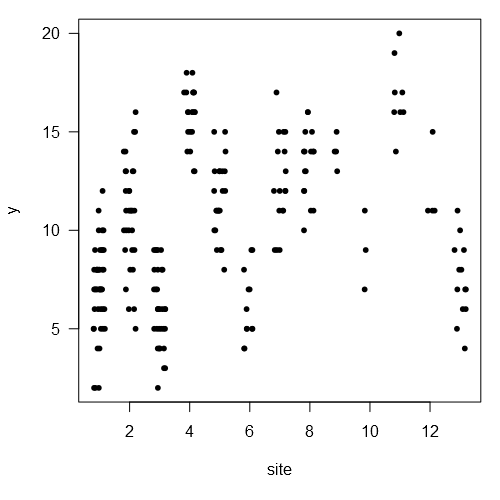
fit <- jags(list(y=y, site=site), NULL, c('sd', 'alpha', 'p'), M, 3, 1000)
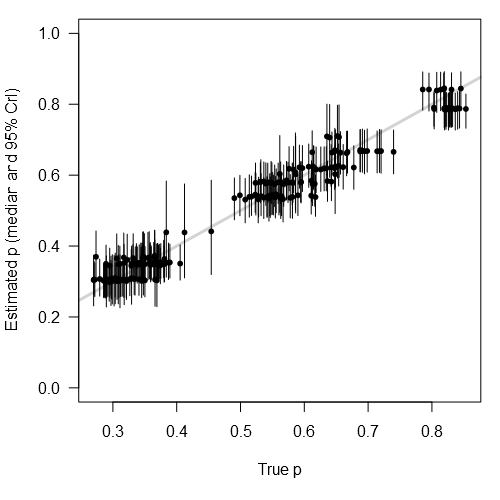
Сравнивая нашу правду p по оценкам JAGS:
plot(plogis(logit.p), fit$BUGSoutput$summary[
grep('^p\\[', row.names(fit$BUGSoutput$summary)), '50%'], pch=20,
xlab='True p', ylab='Estimated p (median and 95% CrI)', las=1, ylim=c(0, 1),
panel.first=abline(0, 1, lwd=3, col='light gray'))
segments(plogis(logit.p),
fit$BUGSoutput$summary[
grep('^p\\[', row.names(fit$BUGSoutput$summary)), '2.5%'],
y1=fit$BUGSoutput$summary[
grep('^p\\[', row.names(fit$BUGSoutput$summary)), '97.5%'])
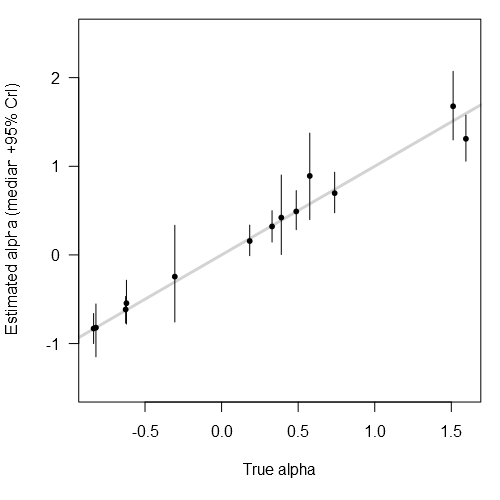
И альфа:
plot(alpha, fit$BUGSoutput$summary[
grep('^alpha\\[', row.names(fit$BUGSoutput$summary)), '50%'], pch=20,
xlab='True alpha', ylab='Estimated alpha (median +95% CrI)', las=1,
ylim=c(-1.5, 2.5), panel.first=abline(0, 1, lwd=3, col='light gray'))
segments(alpha,
fit$BUGSoutput$summary[
grep('^alpha\\[', row.names(fit$BUGSoutput$summary)), '2.5%'],
y1=fit$BUGSoutput$summary[
grep('^alpha\\[', row.names(fit$BUGSoutput$summary)), '97.5%'])
Сводные данные (например, квантили) легко извлекаются из сохраненных выборок, и некоторые из них уже представлены в сводке JAGS (т.е. fit$BUGSoutput$summary). В вашем случае вас, вероятно, интересуют квантили для оценок alpha (т. е. среднее место на сайте). Другой способ доступа к ним, и который полезен, когда вы хотите, чтобы квантили еще не рассчитывались R2jags, как следует:
apply(fit$BUGSoutput$sims.list$alpha, 2, quantile, c(0.2, 0.5, 0.8))
# [,1] [,2] [,3] [,4] [,5] [,6] [,7]
# 20% -0.6753085 0.08214699 -0.8994924 1.213293 0.2411191 -0.9441959 0.4038927
# 50% -0.6151128 0.15716925 -0.8299434 1.310542 0.3214097 -0.8205142 0.4909790
# 80% -0.5461859 0.23436643 -0.7632734 1.405498 0.3994087 -0.6982591 0.5887423
# [,8] [,9] [,10] [,11] [,12] [,13]
# 20% 0.6052447 0.6722630 -0.46050504 1.513086 0.2352861 -0.6516170
# 50% 0.6971180 0.8914973 -0.24458871 1.677613 0.4217723 -0.5443512
# 80% 0.7858756 1.1142837 -0.01018129 1.839783 0.6183198 -0.4309478
Возможно, вы захотите рассмотреть иерархический подход, в соответствии с которым alpha взяты из популяции альф, которые относятся к общему распространению. Это будет включать что-то вроде:
M <- function() {
for (j in 1:13){
alpha[j] ~ dnorm(mean.alpha, sd.alpha^-2)
}
for (i in 1:length(y)) {
y[i] ~ dbin(p[i], 20)
logit(p[i]) <- alpha[site[i]] + eps[i]
eps[i] ~ dnorm(0, sd^-2)
}
sd ~ dunif(0, 100)
mean.alpha ~ dnorm(0, 0.0001)
sd.alpha ~ dunif(0, 100)
}
Это тогда скажет вам кое-что о разнице между сайтами в групповом средстве (т.е. путем проверки sd.alpha). Вы также можете рассмотреть возможность sd (т. е. разница между наблюдениями на сайтах) может варьироваться в зависимости от сайта, хотя у вас может быть слишком мало данных для этого (и, возможно, совершенно разумно иметь одну постоянную sd во всяком случае... зависит от системы).