Примерка кривой питон

Question

У меня есть несколько точек, и я пытаюсь подобрать кривую для этих точек. Я знаю что существуют scipy.optimize.curve_fit функция, но я не понимаю документацию, т.е. как использовать эту функцию.

Мои очки: np.array([(1, 1), (2, 4), (3, 1), (9, 3)])

Кто-нибудь может объяснить, как это сделать?

Answer 1

Я предлагаю вам начать с простой полиномиальной подгонки, scipy.optimize.curve_fit пытается соответствовать функции f что вы должны знать множество пунктов.

Это простое 3-градусное полиномиальное соответствие numpy.polyfit а также poly1dпервый выполняет полиномиальное соответствие наименьших квадратов, а второй вычисляет новые точки:

import numpy as np
import matplotlib.pyplot as plt

points = np.array([(1, 1), (2, 4), (3, 1), (9, 3)])
# get x and y vectors
x = points[:,0]
y = points[:,1]

# calculate polynomial
z = np.polyfit(x, y, 3)
f = np.poly1d(z)

# calculate new x's and y's
x_new = np.linspace(x[0], x[-1], 50)
y_new = f(x_new)

plt.plot(x,y,'o', x_new, y_new)
plt.xlim([x[0]-1, x[-1] + 1 ])
plt.show()

Answer 2

Сначала вам нужно разделить массив numpy на два отдельных массива, содержащих значения x и y.

x = [1, 2, 3, 9]
y = [1, 4, 1, 3]

Curve_fit также требует функции, которая обеспечивает тип соответствия, который вы хотели бы. Например, линейное соответствие будет использовать такую ​​функцию, как

def func(x, a, b):
    return a*x + b

scipy.optimize.curve_fit(func, x, y) вернет пустой массив, содержащий два массива: первый будет содержать значения для a а также b это лучше всего соответствует вашим данным, и второй будет ковариация параметров оптимального соответствия.

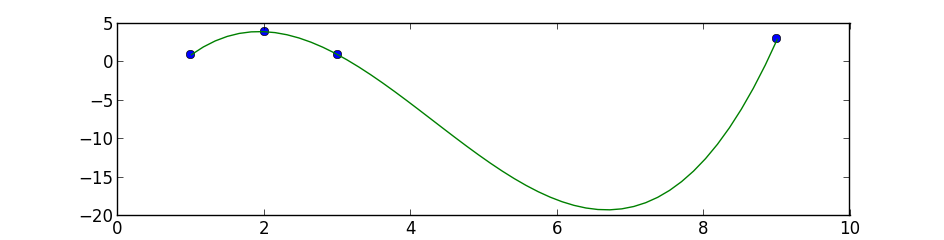
Вот пример линейного соответствия с предоставленными вами данными.

import numpy as np
from scipy.optimize import curve_fit

x = np.array([1, 2, 3, 9])
y = np.array([1, 4, 1, 3])

def fit_func(x, a, b):
    return a*x + b

params = curve_fit(fit_func, x, y)

[a, b] = params[0]

Этот код вернется a = 0.135483870968 а также b = 1.74193548387

Вот график с вашими точками и линейным подбором... который явно плохой, но вы можете изменить функцию подбора, чтобы получить любой тип подгонки, который вы хотели бы.

Answer 3

np.polyfitподбирает полиномиальную функцию к данным (что всегда является хорошей отправной точкой), ноscipy.optimize.curve_fitгораздо более гибок, потому что вы можете подогнать к данным любую функцию, которую хотите ( Грег также упоминает об этом).

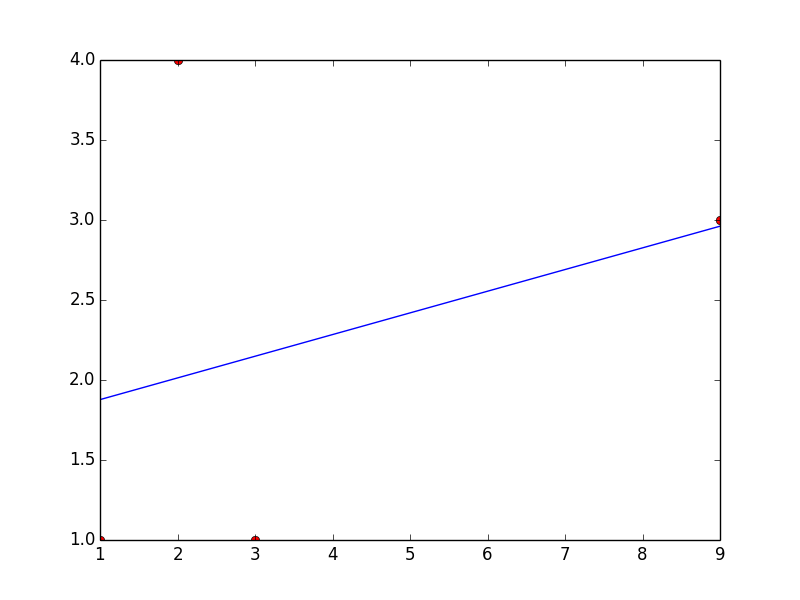
Например, чтобы подобрать полиномиальную функцию степени 3, инициализируйте полиномиальную функцию и передайте ее для вычисления ее коэффициентов с использованием обучающих значений и . Как только у вас естьcoefs_poly3dвычислены, вы можете подключить другие значения, чтобы сгенерировать подходящие значения и построить общую функцию «вокруг» исходных обучающих значений. Следующий код создает тот же самый график в сообщении jabaldonedo.

      def poly3d(x, a, b, c, d):
    return a + b*x + c*x**2 + d*x**3

# initial data to fit
x, y = np.array([(1, 1), (2, 4), (3, 1), (9, 3)]).T
# fit poly3d to x, y
coefs_poly3d, _ = curve_fit(poly3d, x, y)

# initialize some points
x_data = np.linspace(min(x), max(x), 50)
# transform x_data to y-axis values via poly3d
y_data = poly3d(x_data, *coefs_poly3d)
# plot the points
plt.plot(x, y, 'ro', x_data, y_data);

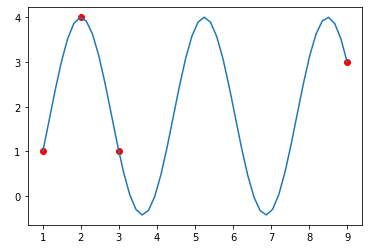
Как упоминалось ранее, является более гибким в том смысле, что вы можете использовать любую функцию. Например, глядя на данные, кажется, что мы можем подобрать и синусоидальную функцию. Затем просто инициализируйте синусоидальную функцию и передайте ее для вычисленияcoefs_sine.

Обратите внимание, что посколькуcurve_fitявляется итеративным алгоритмом, выбирающим подходящее начальное предположение для параметров (a,b,c,d) иногда имеет решающее значение для сходимости алгоритма. В приведенном ниже примере он инициализируетсяp0=[0, 0, -2, 0]. Вы можете, конечно, сделать обоснованное предположение методом проб и ошибок, нанеся данные с разными коэффициентами.

      def sine(x, a, b, c, d):
    return a + b*np.sin(-x*c + d)

# fit data to `sine` function
coefs_sine, _ = curve_fit(sine, x, y, p0=[0, 0, -2, 0])

Используя ту же настройку, что и раньше (x,yиx_dataопределяется как в случае), дает следующий график:

Какая функция лучше соответствует данным?

Распространенным способом проверки согласия является сравнение среднеквадратичной ошибки (т.е. MSE) подобранных значений. В основном он вычисляет, насколько далеко от фактических данных находятся подогнанные значения; ближе, тем лучше, поэтому небольшие значения MSE — это хорошо. Для рассматриваемого примера, если мы сравним MSE двух функций ( иpoly3d),sineлучше соответствует данным (поскольку его MSE меньше).

      def mse(func, x, y, coefs):
    return np.mean((func(x, *coefs) - y)**2)

mse_sine = mse(sine, x, y, coefs_sine)
mse_poly3d = mse(poly3d, x, y, coefs_poly3d)

NB Этот пост посвящен только подгонке функции к существующим данным. Не было предпринято никаких попыток построить прогностические модели (в этом случае то, как работает функция, зависит от того, как она работает с невидимыми данными, и обе функции здесь, вероятно, очень переобучены).