Квадратичная кривая Безье: вычисление точек
Я хотел бы рассчитать точку на квадратичной кривой. Чтобы использовать его с элементом canvas HTML5.
Когда я использую quadraticCurveTo() Функция в JavaScript, у меня есть исходная точка, целевая точка и контрольная точка.
Как я могу рассчитать точку на созданной квадратичной кривой, скажем, t=0.5 с "только" зная это три очка?
4 ответа
Используйте квадратную формулу Безье, найденную, например, на странице Википедии для Кривых Безье:
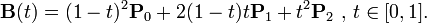
В псевдокоде это
t = 0.5; // given example value
x = (1 - t) * (1 - t) * p[0].x + 2 * (1 - t) * t * p[1].x + t * t * p[2].x;
y = (1 - t) * (1 - t) * p[0].y + 2 * (1 - t) * t * p[1].y + t * t * p[2].y;
p[0] является отправной точкой, p[1] контрольная точка, и p[2] это конечная точка. t это параметр, который идет от 0 до 1.
Если кому-то нужна кубическая форма:
//B(t) = (1-t)**3 p0 + 3(1 - t)**2 t P1 + 3(1-t)t**2 P2 + t**3 P3
x = (1-t)*(1-t)*(1-t)*p0x + 3*(1-t)*(1-t)*t*p1x + 3*(1-t)*t*t*p2x + t*t*t*p3x;
y = (1-t)*(1-t)*(1-t)*p0y + 3*(1-t)*(1-t)*t*p1y + 3*(1-t)*t*t*p2y + t*t*t*p3y;
В случае, если кому-то нужна n-я форма, вот алгоритм. Вы кормите его N точек, и он вернет массив N + (N-1) + (N-2) ... указывает, это решает (N * (N*1)) / 2, Последняя точка - это позиция на кривой для заданного значения T.
9
7 8
4 5 6
0 1 2 3
Вы бы подали алгоритм 0 1 2 3 в качестве контрольных точек, и эти позиции были бы остальной частью массива. Последняя точка (9) - это значение, которое вы хотите.
Это также, как вы подразделяете кривую Безье, вы даете ему значение t затем вы объявляете подразделенную кривую сторонами пирамиды. Затем вы индексируете различные точки на стороне пирамиды и на другой стороне пирамиды, построенной из основания. Так, например, в квинтике:
E
C D
9 A B
5 6 7 8
0 1 2 3 4
(Простите за гекс, я хотел, чтобы это было довольно)
Вы должны индексировать две идеально разделенные кривые в 0, 5, 9, C, E и E, D, B, 8, 4. Обратите особое внимание, чтобы первая кривая начиналась с контрольной точки (0) и заканчивалась в точке на кривой (E), а вторая кривая начинается на кривой (E) и заканчивается в контрольной точке (4). Учитывая это, вы можете идеально разделить кривую Безье, это то, что вы ожидаете. Новая контрольная точка, связывающая две кривые, находится на кривой.
/**
* Performs deCasteljau's algorithm for a bezier curve defined by the given control points.
*
* A cubic for example requires four points. So it should get at least an array of 8 values
*
* @param controlpoints (x,y) coord list of the Bezier curve.
* @param returnArray Array to store the solved points. (can be null)
* @param t Amount through the curve we are looking at.
* @return returnArray
*/
public static float[] deCasteljau(float[] controlpoints, float[] returnArray, float t) {
int m = controlpoints.length;
int sizeRequired = (m/2) * ((m/2) + 1);
if (returnArray == null) returnArray = new float[sizeRequired];
if (sizeRequired > returnArray.length) returnArray = Arrays.copyOf(controlpoints, sizeRequired); //insure capacity
else System.arraycopy(controlpoints,0,returnArray,0,controlpoints.length);
int index = m; //start after the control points.
int skip = m-2; //skip if first compare is the last control point.
for (int i = 0, s = returnArray.length - 2; i < s; i+=2) {
if (i == skip) {
m = m - 2;
skip += m;
continue;
}
returnArray[index++] = (t * (returnArray[i + 2] - returnArray[i])) + returnArray[i];
returnArray[index++] = (t * (returnArray[i + 3] - returnArray[i + 1])) + returnArray[i + 1];
}
return returnArray;
}
Вы заметите, что это просто формула для суммы через каждый набор очков. Для N решений вы получаете (N-1) средние точки при значении (t), затем вы берете средние точки из них и получаете (N-2) баллов, затем (N-3) баллов и т. Д., Пока у вас не будет только одной точки. Эта точка находится на кривой. Таким образом, решение для значений между 0, 1 для t, даст вам всю кривую. Зная это, моя реализация просто передает значения вперед в массиве, сохраняя при этом пересчет чего-либо более одного раза. Я использовал его для сотен очков, и это все еще молниеносно.
(на случай, если вам интересно, нет, это не стоит того. SVG прав, остановившись на кубике).
Я создал это демо:
// x = a * (1-t)³ + b * 3 * (1-t)²t + c * 3 * (1-t)t² + d * t³
//------------------------------------------------------------
// x = a - 3at + 3at² - at³
// + 3bt - 6bt² + 3bt³
// + 3ct² - 3ct³
// + dt³
//--------------------------------
// x = - at³ + 3bt³ - 3ct³ + dt³
// + 3at² - 6bt² + 3ct²
// - 3at + 3bt
// + a
//--------------------------------
// 0 = t³ (-a+3b-3c+d) + => A
// t² (3a-6b+3c) + => B
// t (-3a+3b) + => c
// a - x => D
//--------------------------------
var A = d - 3*c + 3*b - a,
B = 3*c - 6*b + 3*a,
C = 3*b - 3*a,
D = a-x;
// So we need to solve At³ + Bt² + Ct + D = 0
может помочь кому-то
Я отредактировал ответ talkhabis (кубическая кривая), чтобы кривая отображалась с правильными координатами. (Не могу комментировать) Необходимо было изменить координаты Y (-p[]. Y +150). (Новая переменная для этого может быть более хорошим и эффективным решением, но вы поняли идею)
// Apply points to SVG and create the curve and controllers :
var path = document.getElementById('path'),
ctrl1 = document.getElementById('ctrl1'),
ctrl2 = document.getElementById('ctrl2'),
D = 'M ' + p0.x + ' ' + (-p0.y+150) +
'C ' + c0.x + ' ' + (-c0.y+150) +', ' + c1.x + ' ' + (-c1.y+150) + ', ' + p1.x + ' ' + (-p1.y+150);
path.setAttribute('d',D);
ctrl1.setAttribute('d','M'+p0.x+','+(-p0.y+150)+'L'+c0.x+','+(-c0.y+150));
ctrl2.setAttribute('d','M'+p1.x+','+(-p1.y+150)+'L'+c1.x+','+(-c1.y+150));
// Lets test the "Bezier Function"
var t = 0, point = document.getElementById('point');
setInterval(function(){
var p = Bezier(p0,c0,c1,p1,t);
point.setAttribute('cx',p.x);
point.setAttribute('cy',-p.y+150);
t += 0.01;
if(t>=1) t=0;
},50);
// OK ... Now tring to get "y" on cruve based on mouse "x" :
var svg = document.getElementById('svg'),
point2 = document.getElementById('point2');
svg.onmousemove = function(e){
var x = (e.pageX - 50)/2,
y = (e.pageY - 50)/2;
// "-50" because of "50px margin" on the left side
// and "/2" because the svg width is 300 units and 600 px => 300 = 600/2
// Get the x,y by mouse x
var p = YBX(p0,c0,c1,p1,x);
point2.setAttribute('cx',p.x);
point2.setAttribute('cy',-p.y+150);
}
http://jsfiddle.net/u214gco8/1/
Я также создал C-код, чтобы проверить результаты для кубической кривой. Просто введите координаты X и Y в основной функции.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
void bezierCurve(int x[] , int y[])
{
double xu = 0.0 , yu = 0.0 , u = 0.0 ;
int i = 0 ;
for(u = 0.0 ; u <= 1.0 ; u += 0.05)
{
xu = pow(1-u,3)*x[0]+3*u*pow(1-u,2)*x[1]+3*pow(u,2)*(1-u)*x[2]
+pow(u,3)*x[3];
yu = pow(1-u,3)*y[0]+3*u*pow(1-u,2)*y[1]+3*pow(u,2)*(1-u)*y[2]
+pow(u,3)*y[3];
printf("X: %i Y: %i \n" , (int)xu , (int)yu) ;
}
}
int main(void) {
int x[] = {0,75,50,300};
int y[] = {0,2,140,100};
bezierCurve(x,y);
return 0;
}
Просто примечание: если вы используете обычные формулы, представленные здесь, то не ожидайте, что t = 0,5 вернет точку на половине длины кривой. В большинстве случаев это не так.
Подробнее об этом здесь в разделе "§23 - Трассировка кривой через фиксированные интервалы расстояний" и здесь.