Какова цель сетки в Python / NumPy?
Может кто-нибудь объяснить мне, какова цель meshgrid функционировать в Numpy? Я знаю, что это создает какую-то сетку координат для построения графиков, но я не вижу прямой выгоды от этого.
Я изучаю "Машинное обучение Python" у Себастьяна Рашки, и он использует его для построения границ решений. Смотрите ввод 11 здесь.
Я также попробовал этот код из официальной документации, но, опять же, вывод не имеет для меня никакого смысла.
x = np.arange(-5, 5, 1)
y = np.arange(-5, 5, 1)
xx, yy = np.meshgrid(x, y, sparse=True)
z = np.sin(xx**2 + yy**2) / (xx**2 + yy**2)
h = plt.contourf(x,y,z)
Пожалуйста, если возможно, также покажите мне много реальных примеров.
10 ответов
Цель meshgrid это создать прямоугольную сетку из массива значений x и массива значений y.
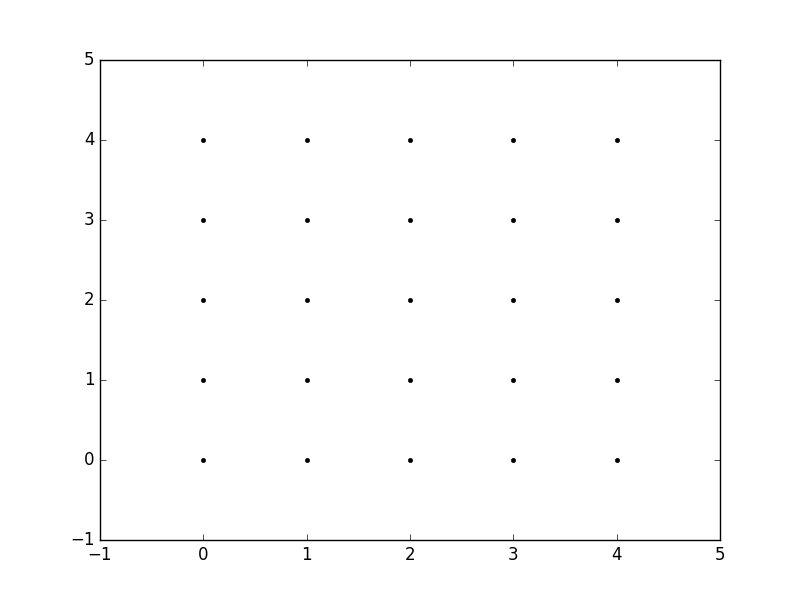
Так, например, если мы хотим создать сетку, в которой у нас есть точка при каждом целочисленном значении между 0 и 4 в обоих направлениях x и y. Чтобы создать прямоугольную сетку, нам нужна каждая комбинация x а также y точки.
Это будет 25 очков, верно? Поэтому, если мы хотим создать массив x и y для всех этих точек, мы можем сделать следующее.
x[0,0] = 0 y[0,0] = 0
x[0,1] = 1 y[0,1] = 0
x[0,2] = 2 y[0,2] = 0
x[0,3] = 3 y[0,3] = 0
x[0,4] = 4 y[0,4] = 0
x[1,0] = 0 y[1,0] = 1
x[1,1] = 1 y[1,1] = 1
...
x[4,3] = 3 y[4,3] = 4
x[4,4] = 4 y[4,4] = 4
Это приведет к следующему x а также y матрицы, такие, что спаривание соответствующего элемента в каждой матрице дает координаты x и y точки в сетке.
x = 0 1 2 3 4 y = 0 0 0 0 0
0 1 2 3 4 1 1 1 1 1
0 1 2 3 4 2 2 2 2 2
0 1 2 3 4 3 3 3 3 3
0 1 2 3 4 4 4 4 4 4
Затем мы можем построить их, чтобы убедиться, что они являются сеткой:
plt.plot(x,y, marker='.', color='k', linestyle='none')
Очевидно, что это становится очень утомительным, особенно для больших диапазонов x а также y, Вместо, meshgrid на самом деле может сгенерировать это для нас: все, что мы должны указать, это x а также y ценности.
xvalues = np.array([0, 1, 2, 3, 4]);
yvalues = np.array([0, 1, 2, 3, 4]);
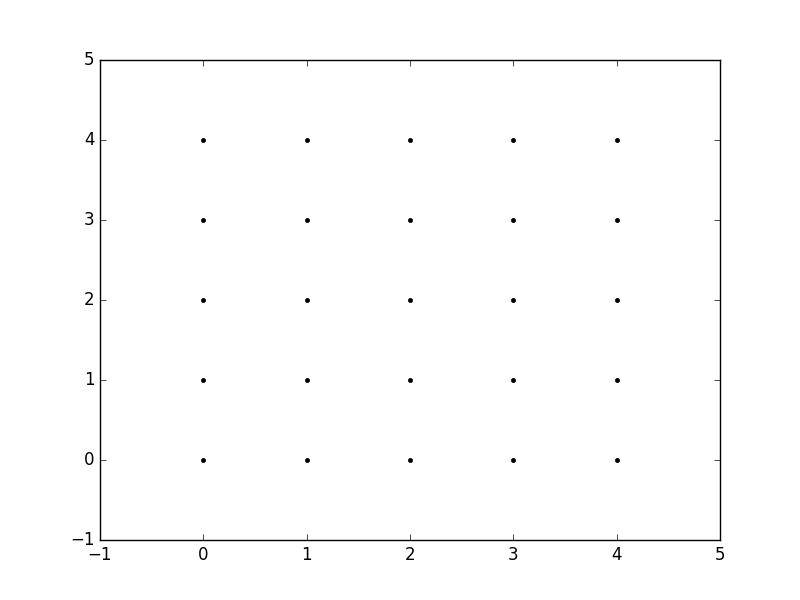
Теперь, когда мы звоним meshgrid мы получаем предыдущий вывод автоматически.
xx, yy = np.meshgrid(xvalues, yvalues)
plt.plot(xx, yy, marker='.', color='k', linestyle='none')
Создание этих прямоугольных сеток полезно для ряда задач. В примере, который вы предоставили в своем посте, это просто способ попробовать функцию (sin(x**2 + y**2) / (x**2 + y**2)) в диапазоне значений для x а также y,
Поскольку эта функция была выбрана на прямоугольной сетке, функцию теперь можно визуализировать как "изображение".
Кроме того, теперь результат можно передать функциям, которые ожидают данные в прямоугольной сетке (т.е. contourf)
На самом деле цель np.meshgrid уже упоминается в документации:
np.meshgridВернуть координатные матрицы из координатных векторов.
Создайте ND координатные массивы для векторизованных вычислений ND скалярных / векторных полей над ND сетками, учитывая одномерные координатные массивы x1, x2,..., xn.
Поэтому его основная цель состоит в создании координатных матриц.
Вы, наверное, просто спросили себя:
Зачем нам нужно создавать координатные матрицы?
Причина, по которой вам нужны координатные матрицы с Python/NumPy, заключается в том, что нет прямой связи между координатами и значениями, за исключением случаев, когда ваши координаты начинаются с нуля и являются чисто положительными целыми числами. Тогда вы можете просто использовать индексы массива в качестве индекса. Однако, когда это не так, вам нужно как-то хранить координаты вместе с вашими данными. Вот где приходят сетки.
Предположим, ваши данные:
1 2 1
2 5 2
1 2 1
Однако каждое значение представляет область шириной 2 километра по горизонтали и 3 километра по вертикали. Предположим, ваше происхождение - это верхний левый угол, и вы хотите, чтобы массивы представляли расстояние, которое вы могли бы использовать:
import numpy as np
h, v = np.meshgrid(np.arange(3)*3, np.arange(3)*2)
где h является:
0 2 4
0 2 4
0 2 4
и ч:
0 0 0
3 3 3
6 6 6
Итак, если у вас есть два индекса, скажем, x а также y (вот почему возвращаемое значение meshgrid обычно xx или же xs вместо x в этом случае я выбрал h по горизонтали!) тогда вы можете получить координату x точки, координату y точки и значение в этой точке, используя:
h[x, y] # horizontal coordinate
v[x, y] # vertical coordinate
data[x, y] # value
Это значительно облегчает отслеживание координат и (что еще более важно) вы можете передавать их функциям, которые должны знать координаты.
Немного более длинное объяснение
Тем не мение, np.meshgrid сам по себе не часто используется напрямую, в основном один просто использует один из похожих объектов np.mgrid или же np.ogrid, Вот np.mgrid представляет sparse=False а также np.ogrid sparse=True случай (я имею в виду sparse аргумент np.meshgrid). Обратите внимание, что существует значительная разница между np.meshgrid а также np.ogrid а также np.mgrid: Первые два возвращаемых значения (если их два или более) меняются местами. Часто это не имеет значения, но вы должны давать значимые имена переменных в зависимости от контекста. Например, в случае двумерной сетки и matplotlib.pyplot.imshow имеет смысл назвать первый возвращенный элемент np.meshgridx и второй y в то время как это наоборот np.mgrid а также np.ogrid,
np.ogrid и разреженные сетки
>>> import numpy as np
>>> yy, xx = np.ogrid[-5:6, -5:6]
>>> xx
array([[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]])
>>> yy
array([[-5],
[-4],
[-3],
[-2],
[-1],
[ 0],
[ 1],
[ 2],
[ 3],
[ 4],
[ 5]])
Как уже было сказано, выходной сигнал обратный по сравнению с np.meshgrid поэтому я распаковал его как yy, xx вместо xx, yy:
>>> xx, yy = np.meshgrid(np.arange(-5, 6), np.arange(-5, 6), sparse=True)
>>> xx
array([[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]])
>>> yy
array([[-5],
[-4],
[-3],
[-2],
[-1],
[ 0],
[ 1],
[ 2],
[ 3],
[ 4],
[ 5]])
Это уже выглядит как координаты, в частности, линии x и y для 2D-графиков.
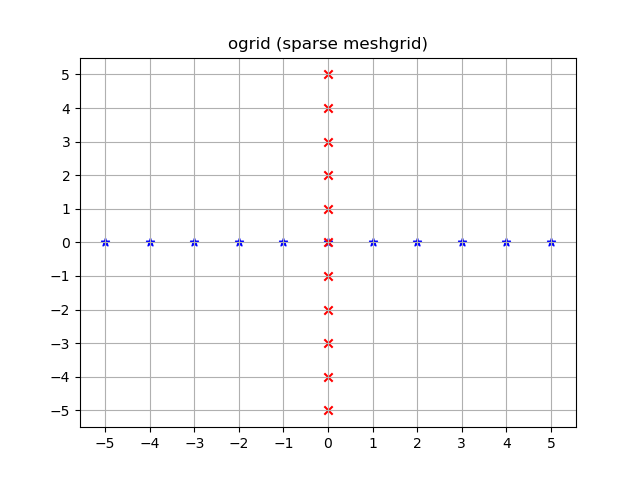
Визуализация:
yy, xx = np.ogrid[-5:6, -5:6]
plt.figure()
plt.title('ogrid (sparse meshgrid)')
plt.grid()
plt.xticks(xx.ravel())
plt.yticks(yy.ravel())
plt.scatter(xx, np.zeros_like(xx), color="blue", marker="*")
plt.scatter(np.zeros_like(yy), yy, color="red", marker="x")
np.mgrid и плотные / плотные сетки
>>> yy, xx = np.mgrid[-5:6, -5:6]
>>> xx
array([[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]])
>>> yy
array([[-5, -5, -5, -5, -5, -5, -5, -5, -5, -5, -5],
[-4, -4, -4, -4, -4, -4, -4, -4, -4, -4, -4],
[-3, -3, -3, -3, -3, -3, -3, -3, -3, -3, -3],
[-2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2],
[ 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3],
[ 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4],
[ 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]])
То же самое применимо и здесь: вывод обратный по сравнению с np.meshgrid:
>>> xx, yy = np.meshgrid(np.arange(-5, 6), np.arange(-5, 6))
>>> xx
array([[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5],
[-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5]])
>>> yy
array([[-5, -5, -5, -5, -5, -5, -5, -5, -5, -5, -5],
[-4, -4, -4, -4, -4, -4, -4, -4, -4, -4, -4],
[-3, -3, -3, -3, -3, -3, -3, -3, -3, -3, -3],
[-2, -2, -2, -2, -2, -2, -2, -2, -2, -2, -2],
[-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[ 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2],
[ 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3],
[ 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4],
[ 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5]])
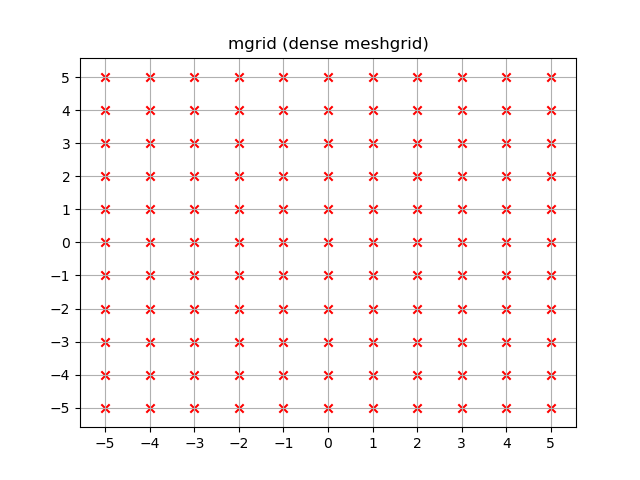
В отличие от ogrid эти массивы содержат все xx а также yy координаты в -5 <= xx <= 5; -5 <= yy <= 5 сетки.
yy, xx = np.mgrid[-5:6, -5:6]
plt.figure()
plt.title('mgrid (dense meshgrid)')
plt.grid()
plt.xticks(xx[0])
plt.yticks(yy[:, 0])
plt.scatter(xx, yy, color="red", marker="x")
функциональность
Это не только 2D, эти функции работают для произвольных измерений (ну, в Python есть максимальное количество аргументов для функции и максимальное количество измерений, которое допускает NumPy):
>>> x1, x2, x3, x4 = np.ogrid[:3, 1:4, 2:5, 3:6]
>>> for i, x in enumerate([x1, x2, x3, x4]):
... print('x{}'.format(i+1))
... print(repr(x))
x1
array([[[[0]]],
[[[1]]],
[[[2]]]])
x2
array([[[[1]],
[[2]],
[[3]]]])
x3
array([[[[2],
[3],
[4]]]])
x4
array([[[[3, 4, 5]]]])
>>> # equivalent meshgrid output, note how the first two arguments are reversed and the unpacking
>>> x2, x1, x3, x4 = np.meshgrid(np.arange(1,4), np.arange(3), np.arange(2, 5), np.arange(3, 6), sparse=True)
>>> for i, x in enumerate([x1, x2, x3, x4]):
... print('x{}'.format(i+1))
... print(repr(x))
# Identical output so it's omitted here.
Даже если они также работают для 1D, есть две (гораздо более распространенные) функции создания сетки 1D:
np.arangenp.linspace
Кроме start а также stop Аргумент это также поддерживает step аргумент (даже сложные шаги, которые представляют количество шагов):
>>> x1, x2 = np.mgrid[1:10:2, 1:10:4j]
>>> x1 # The dimension with the explicit step width of 2
array([[1., 1., 1., 1.],
[3., 3., 3., 3.],
[5., 5., 5., 5.],
[7., 7., 7., 7.],
[9., 9., 9., 9.]])
>>> x2 # The dimension with the "number of steps"
array([[ 1., 4., 7., 10.],
[ 1., 4., 7., 10.],
[ 1., 4., 7., 10.],
[ 1., 4., 7., 10.],
[ 1., 4., 7., 10.]])
Приложения
Вы специально спросили о цели, и на самом деле эти сетки очень полезны, если вам нужна система координат.
Например, если у вас есть функция NumPy, которая вычисляет расстояние в двух измерениях:
def distance_2d(x_point, y_point, x, y):
return np.hypot(x-x_point, y-y_point)
И вы хотите знать расстояние каждой точки:
>>> ys, xs = np.ogrid[-5:5, -5:5]
>>> distances = distance_2d(1, 2, xs, ys) # distance to point (1, 2)
>>> distances
array([[9.21954446, 8.60232527, 8.06225775, 7.61577311, 7.28010989,
7.07106781, 7. , 7.07106781, 7.28010989, 7.61577311],
[8.48528137, 7.81024968, 7.21110255, 6.70820393, 6.32455532,
6.08276253, 6. , 6.08276253, 6.32455532, 6.70820393],
[7.81024968, 7.07106781, 6.40312424, 5.83095189, 5.38516481,
5.09901951, 5. , 5.09901951, 5.38516481, 5.83095189],
[7.21110255, 6.40312424, 5.65685425, 5. , 4.47213595,
4.12310563, 4. , 4.12310563, 4.47213595, 5. ],
[6.70820393, 5.83095189, 5. , 4.24264069, 3.60555128,
3.16227766, 3. , 3.16227766, 3.60555128, 4.24264069],
[6.32455532, 5.38516481, 4.47213595, 3.60555128, 2.82842712,
2.23606798, 2. , 2.23606798, 2.82842712, 3.60555128],
[6.08276253, 5.09901951, 4.12310563, 3.16227766, 2.23606798,
1.41421356, 1. , 1.41421356, 2.23606798, 3.16227766],
[6. , 5. , 4. , 3. , 2. ,
1. , 0. , 1. , 2. , 3. ],
[6.08276253, 5.09901951, 4.12310563, 3.16227766, 2.23606798,
1.41421356, 1. , 1.41421356, 2.23606798, 3.16227766],
[6.32455532, 5.38516481, 4.47213595, 3.60555128, 2.82842712,
2.23606798, 2. , 2.23606798, 2.82842712, 3.60555128]])
Выходные данные были бы идентичны, если бы они проходили в плотной сетке вместо открытой сетки. Вещание NumPys делает это возможным!
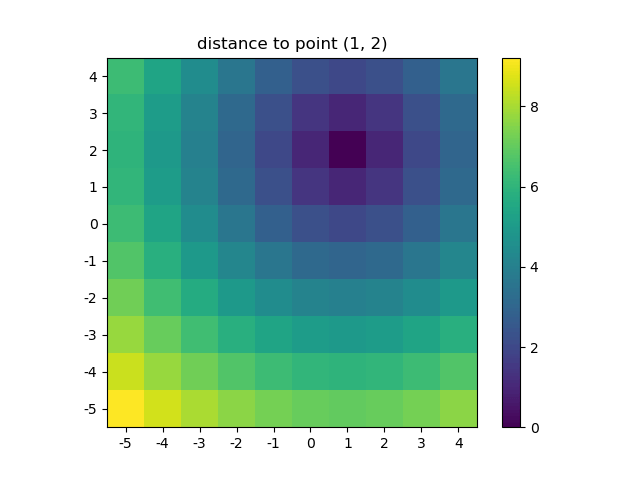
Давайте представим результат:
plt.figure()
plt.title('distance to point (1, 2)')
plt.imshow(distances, origin='lower', interpolation="none")
plt.xticks(np.arange(xs.shape[1]), xs.ravel()) # need to set the ticks manually
plt.yticks(np.arange(ys.shape[0]), ys.ravel())
plt.colorbar()
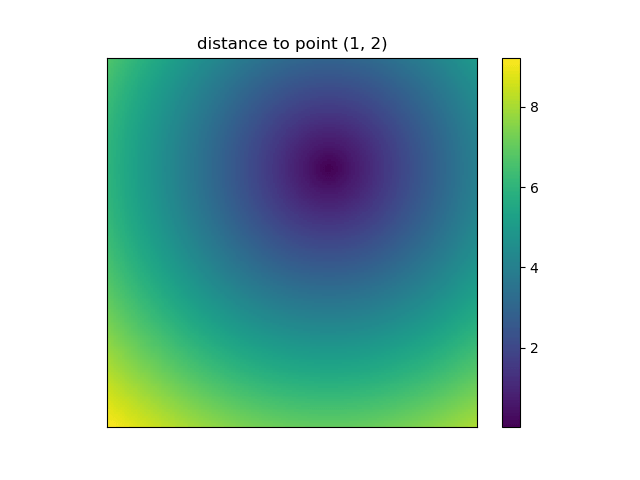
И это также, когда NumPys mgrid а также ogrid стать очень удобным, потому что позволяет легко изменять разрешение ваших сеток:
ys, xs = np.ogrid[-5:5:200j, -5:5:200j]
# otherwise same code as above
Однако так как imshow не поддерживает x а также y входы нужно поменять галочки вручную. Было бы очень удобно, если бы он принял x а также y координаты, верно?
С помощью NumPy легко написать функции, которые естественным образом работают с сетками. Кроме того, в NumPy, SciPy, MatPlotLib есть несколько функций, которые ожидают, что вы перейдете в сетку.
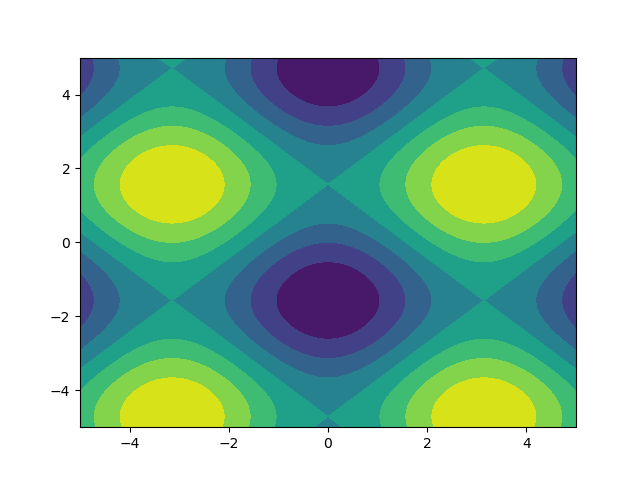
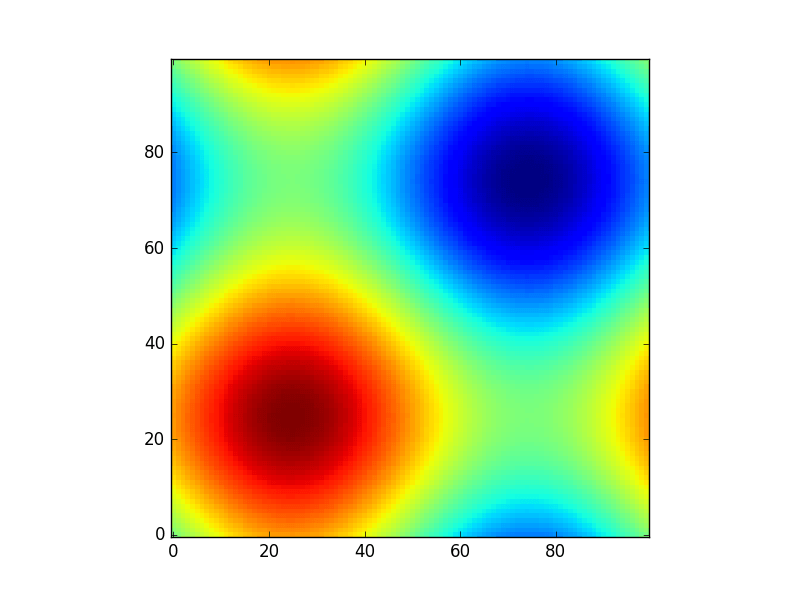
Мне нравятся изображения, поэтому давайте рассмотрим matplotlib.pyplot.contour:
ys, xs = np.mgrid[-5:5:200j, -5:5:200j]
density = np.sin(ys)-np.cos(xs)
plt.figure()
plt.contour(xs, ys, density)
Обратите внимание, что координаты уже правильно установлены! Это было бы не так, если вы только что прошли в density,
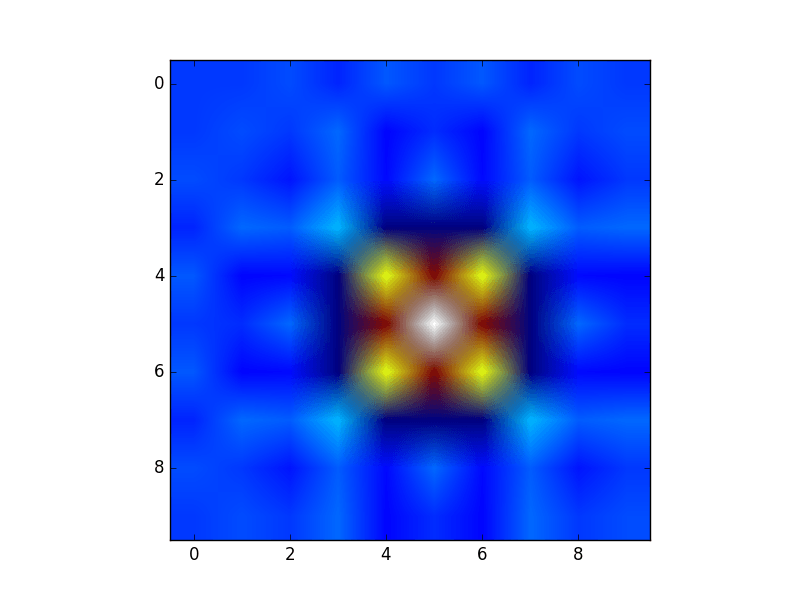
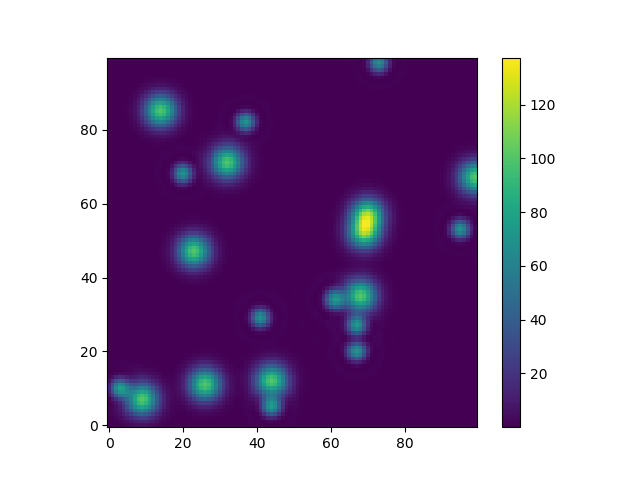
Или приведу еще один забавный пример с использованием моделей астропии (на этот раз меня не волнуют координаты, я просто использую их для создания сетки):
from astropy.modeling import models
z = np.zeros((100, 100))
y, x = np.mgrid[0:100, 0:100]
for _ in range(10):
g2d = models.Gaussian2D(amplitude=100,
x_mean=np.random.randint(0, 100),
y_mean=np.random.randint(0, 100),
x_stddev=3,
y_stddev=3)
z += g2d(x, y)
a2d = models.AiryDisk2D(amplitude=70,
x_0=np.random.randint(0, 100),
y_0=np.random.randint(0, 100),
radius=5)
z += a2d(x, y)
Хотя это просто "для внешнего вида" несколько функций, связанных с функциональными моделями и примеркой (например, scipy.interpolate.interp2d, scipy.interpolate.griddata даже показать примеры использования np.mgrid) в Scipy и т. д. требуются сетки. Большинство из них работают с открытыми сетками и плотными сетками, однако некоторые работают только с одним из них.
Предположим, у вас есть функция:
def sinus2d(x, y):
return np.sin(x) + np.sin(y)
и вы хотите, например, посмотреть, как это выглядит в диапазоне от 0 до 2* пи. Как бы вы это сделали? Там np.meshgrid приходит в:
xx, yy = np.meshgrid(np.linspace(0,2*np.pi,100), np.linspace(0,2*np.pi,100))
z = sinus2d(xx, yy) # Create the image on this grid
и такой сюжет будет выглядеть так:
import matplotlib.pyplot as plt
plt.imshow(z, origin='lower', interpolation='none')
plt.show()
Так np.meshgrid это просто удобство. В принципе то же самое может быть сделано:
z2 = sinus2d(np.linspace(0,2*np.pi,100)[:,None], np.linspace(0,2*np.pi,100)[None,:])
но там вы должны знать о своих измерениях (предположим, у вас есть более двух...) и правильное вещание. np.meshgrid делает все это для вас.
Также meshgrid позволяет вам удалять координаты вместе с данными, если вы, например, хотите выполнить интерполяцию, но исключить определенные значения:
condition = z>0.6
z_new = z[condition] # This will make your array 1D
так как бы вы сейчас сделали интерполяцию? Вы можете дать x а также y к функции интерполяции, как scipy.interpolate.interp2d поэтому вам нужен способ узнать, какие координаты были удалены:
x_new = xx[condition]
y_new = yy[condition]
и тогда вы все еще можете интерполировать с "правильными" координатами (попробуйте без сетки, и у вас будет много дополнительного кода):
from scipy.interpolate import interp2d
interpolated = interp2(x_new, y_new, z_new)
и оригинальная сетка позволяет вам снова получить интерполяцию на исходной сетке:
interpolated_grid = interpolated(xx, yy)
Это всего лишь несколько примеров, где я использовал meshgrid может быть намного больше.
Краткий ответ
Цель
meshgridпомогает заменить циклы Python (медленно интерпретируемый код) векторизованными операциями в библиотеке C NumPy.
Заимствовано с этого сайта.
x = np.arange(-4, 4, 0.25)
y = np.arange(-4, 4, 0.25)
X, Y = np.meshgrid(x, y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
meshgridиспользуется для создания пар координат от -4 до +4 с шагом 0,25 в каждом направлении X и Y. Затем каждая пара используется для нахождения R и Z из нее. Этот способ подготовки "сетки" координат часто используется при построении 3D-поверхностей или раскрашивании 2D-поверхностей.
Подробности: Python for-loop против векторной операции NumPy
Чтобы взять более простой пример, предположим, что у нас есть две последовательности значений,
a = [2,7,9,20]
b = [1,6,7,9]
и мы хотим выполнить операцию с каждой возможной парой значений: одно из первого списка, другое из второго. Мы также хотим сохранить результат. Например, предположим, что мы хотим получить сумму значений для каждой возможной пары.
Медленный и кропотливый метод
c = []
for i in range(len(b)):
row = []
for j in range(len(a)):
row.append (a[j] + b[i])
c.append (row)
print (c)
Результат:
[[3, 8, 10, 21],
[8, 13, 15, 26],
[9, 14, 16, 27],
[11, 16, 18, 29]]
Python интерпретируется, эти циклы относительно медленно выполняются.
Быстрый и легкий способ
meshgridпредназначен для устранения зацикливания кода. Он возвращает два массива (i и j ниже), которые можно объединить для сканирования всех существующих пар следующим образом:
i,j = np.meshgrid (a,b)
c = i + j
print (c)
Результат:
[[ 3 8 10 21]
[ 8 13 15 26]
[ 9 14 16 27]
[11 16 18 29]]
Сетка под капотом
Два массива, подготовленные
meshgrid находятся:
(array([[ 2, 7, 9, 20],
[ 2, 7, 9, 20],
[ 2, 7, 9, 20],
[ 2, 7, 9, 20]]),
array([[1, 1, 1, 1],
[6, 6, 6, 6],
[7, 7, 7, 7],
[9, 9, 9, 9]]))
Эти массивы создаются путем повторения предоставленных значений. Один содержит значения в идентичных строках, другой - другие значения в идентичных столбцах. Количество строк и столбцов определяется количеством элементов в другой последовательности.
Два массива, созданные
meshgridпоэтому совместимы по форме для векторной операции. Представьте, что последовательности x и y в коде вверху страницы имеют разное количество элементов, результирующие массивы X и Y будут в любом случае совместимы по форме, не требуя какой-либо трансляции.
Происхождение
numpy.meshgridпроисходит из MATLAB, как и многие другие функции NumPy. Так что вы также можете изучить примеры из MATLAB, чтобы увидеть
meshgridпри использовании код для трехмерного построения в MATLAB выглядит так же.
Сетка mesh помогает создать прямоугольную сетку из двух одномерных массивов всех пар точек из двух массивов.
x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 1, 2, 3, 4])
Теперь, если вы определили функцию f(x,y) и хотите применить эту функцию ко всем возможным комбинациям точек из массивов 'x' и 'y', то вы можете сделать это:
f(*np.meshgrid(x, y))
Скажем, если ваша функция просто производит произведение двух элементов, то именно так можно получить декартово произведение, эффективно для больших массивов.
По ссылке здесь
Основная идея
Учитывая возможные значения x, xs, (воспринимайте их как отметки на оси x графика) и возможные значения y, ys, meshgrid генерирует соответствующий набор (x, y) точек сетки --- аналогично set((x, y) for x in xs for y in yx). Например, еслиxs=[1,2,3] а также ys=[4,5,6], мы получили бы набор координат {(1,4), (2,4), (3,4), (1,5), (2,5), (3,5), (1,6), (2,6), (3,6)}.
Форма возвращаемого значения
Однако представление о том, что meshgrid return отличается от приведенного выше выражения двумя способами:
Во-первых,meshgrid размещает точки сетки в 2-м массиве: строки соответствуют различным значениям y, столбцы соответствуют различным значениям x--- как в list(list((x, y) for x in xs) for y in ys), что даст следующий массив:
[[(1,4), (2,4), (3,4)],
[(1,5), (2,5), (3,5)],
[(1,6), (2,6), (3,6)]]
Во-вторых,meshgrid возвращает координаты x и y отдельно (т.е. в двух разных массивах numpy 2d):
xcoords, ycoords = (
array([[1, 2, 3],
[1, 2, 3],
[1, 2, 3]]),
array([[4, 4, 4],
[5, 5, 5],
[6, 6, 6]]))
# same thing using np.meshgrid:
xcoords, ycoords = np.meshgrid([1,2,3], [4,5,6])
# same thing without meshgrid:
xcoords = np.array([xs] * len(ys)
ycoords = np.array([ys] * len(xs)).T
Заметка, np.meshgridможет также создавать сетки для более высоких измерений. Учитывая xs, ys и zs, вы получите обратно xcoords, ycoords, zcoords в виде трехмерных массивов.meshgrid также поддерживает обратный порядок размеров, а также разреженное представление результата.
Приложения
Зачем нам нужна такая форма вывода?
Примените функцию в каждой точке сетки:
одним из мотивов является то, что бинарные операторы, такие как (+, -, *, /, **), перегружены для массивов numpy как поэлементные операции. Это означает, что если у меня есть функцияdef f(x, y): return (x - y) ** 2 который работает с двумя скалярами, я также могу применить его к двум массивам numpy, чтобы получить массив поэлементных результатов: например, f(xcoords, ycoords) или f(*np.meshgrid(xs, ys)) дает следующее в приведенном выше примере:
array([[ 9, 4, 1],
[16, 9, 4],
[25, 16, 9]])
Наружный продукт больших размеров : я не уверен, насколько это эффективно, но вы можете получить такие внешние продукты больших размеров:np.prod(np.meshgrid([1,2,3], [1,2], [1,2,3,4]), axis=0).
Контурные графики в matplotlib: наткнулся наmeshgridпри исследовании рисования контурных графиков с помощью matplotlib для построения границ решений. Для этого вы создаете сетку сmeshgrid, оцените функцию в каждой точке сетки (например, как показано выше), а затем передайте xcoords, ycoords и вычисленные значения f (например, zcoords) в функцию contourf.
За кулисами:
import numpy as np
def meshgrid(x , y):
XX = []
YY = []
for colm in range(len(y)):
XX.append([])
YY.append([])
for row in range(len(x)):
XX[colm].append(x[row])
YY[colm].append(y[colm])
return np.asarray(XX), np.asarray(YY)
В качестве примера возьмем набор данных ответа @Sarsaparilla:
y = [7, 6, 5]
x = [1, 2, 3, 4]
xx, yy = meshgrid(x , y)
и выводит:
>>> xx
array([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
>>> yy
array([[7, 7, 7, 7],
[6, 6, 6, 6],
[5, 5, 5, 5]])
Чтобы создать прямое произведение массивов в NumPy, мы можем использовать функцию meshgrid. Он создает двумерные массивы, содержащие все возможные комбинации элементов из двух исходных массивов.
import numpy as np
# create two arrays
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
# get direct product of arrays
product = np.array(np.meshgrid(arr1, arr2)).T.reshape(-1, 2)
print(product)
и тогда мы получаем:
[[1 4]
[1 5]
[1 6]
[2 4]
[2 5]
[2 6]
[3 4]
[3 5]
[3 6]]
В большинстве случаев вам просто нужно
list(zip(X,Y))куда
X = np.linspace(x)а также
Y = np.linspace(y)