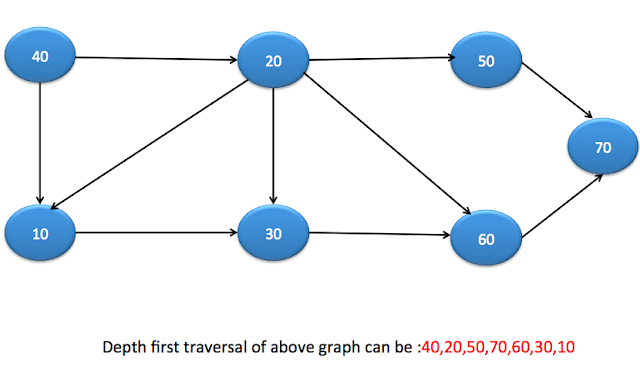
Разница между DFS и BFS в этом примере?

Question

Я немного растерялся после прочтения примеров в DFS, где выходные данные печатаются по-разному для обоих подходов DFS, хотя оба они называются DFS.

Фактически рекурсивный подход DFS печатает выходные данные точно так же, как BFS. Тогда какая разница? Приведенный здесь рекурсивный подход не является примером DFS?

Использование стека

// Iterative DFS using stack
    public  void dfsUsingStack(Node node)
    {
        Stack<Node> stack=new  Stack<Node>();
        stack.add(node);
        node.visited=true;
        while (!stack.isEmpty())
        {
            Node element=stack.pop();
            System.out.print(element.data + " ");

            List<Node> neighbours=element.getNeighbours();
            for (int i = 0; i < neighbours.size(); i++) {
                Node n=neighbours.get(i);
                if(n!=null && !n.visited)
                {
                    stack.add(n);
                    n.visited=true;

                }
            }
        }
    }

Выход 40,20,50,70,60,30,10

Подход рекурсии

// Recursive DFS
    public  void dfs(Node node)
    {
        System.out.print(node.data + " ");
        List neighbours=node.getNeighbours();
        node.visited=true;
        for (int i = 0; i < neighbours.size(); i++) {
            Node n=neighbours.get(i);
            if(n!=null && !n.visited)
            {
                dfs(n);
            }
        }
    }

выход составляет 40,10,20,30,60,50,70, что совпадает с выходом в BFS

Так в чем же разница?

Answer 1

Хотя конечный результат (путь) может быть одинаковым, основная разница между bfs и dfs (а не конкретными опубликованными реализациями) заключается в механизме поиска.
Очевидным примером является случай, когда существует только один путь. В таком случае любой хороший алгоритм поиска (будь то DFS, BFS или другой) в конечном итоге найдет этот путь.
Там, где существует несколько путей, BFS и DFS могут найти один и тот же путь или разные пути. Одна из характеристик bfs заключается в том, что она находит кратчайший путь.
Основное различие в механизме поиска заключается в том, что bfs исследует одинаково во всех направлениях (отсюда и термин "ширина"), в то время как dfs исследует одно (обычно случайное) направление, полностью (отсюда и термин "глубина") и "возврат", если решение не найдено.
Есть много ресурсов, которые показывают визуальное представление bfs и dfs, таких как этот.
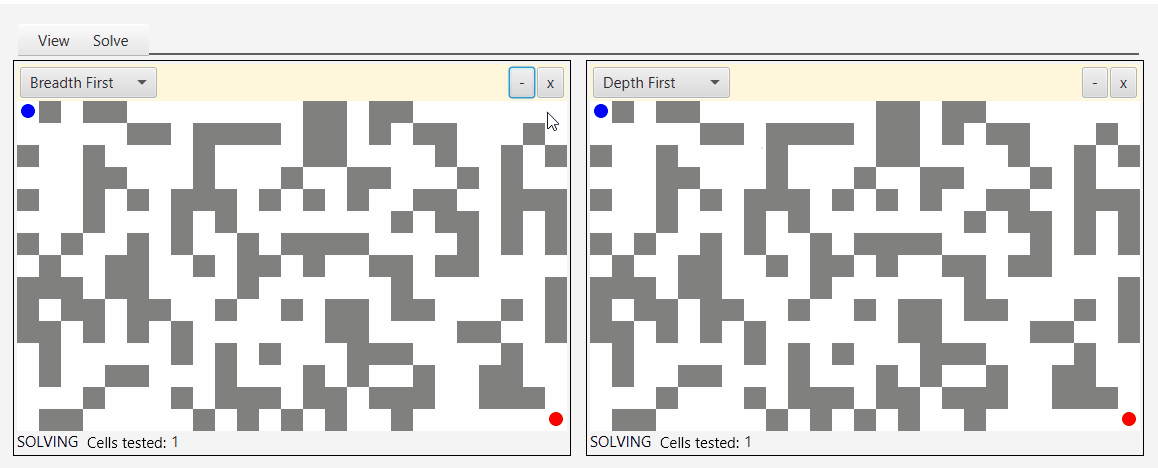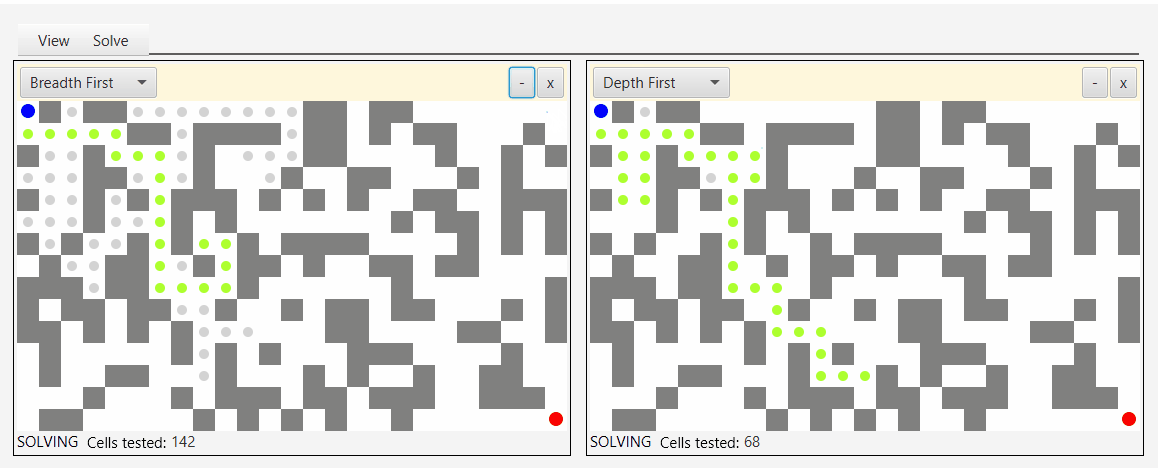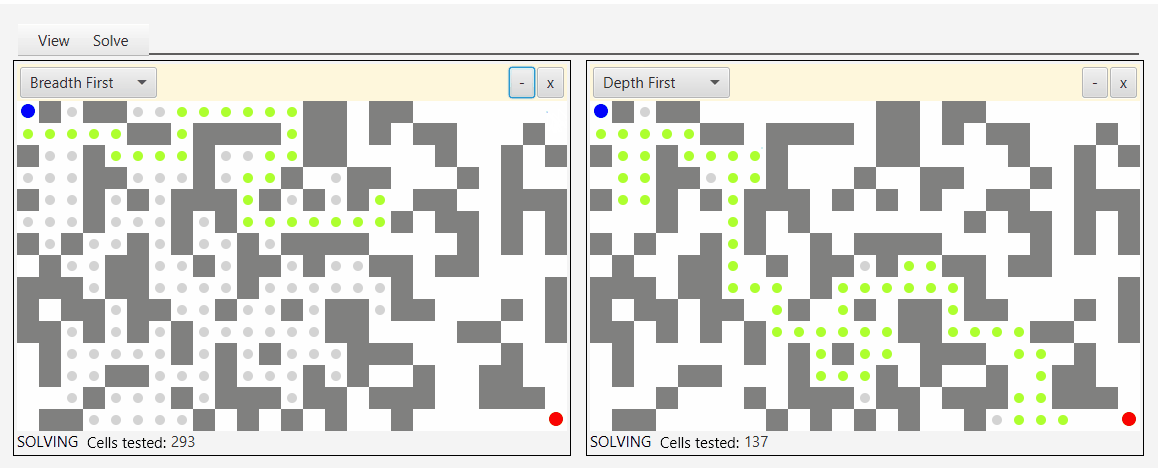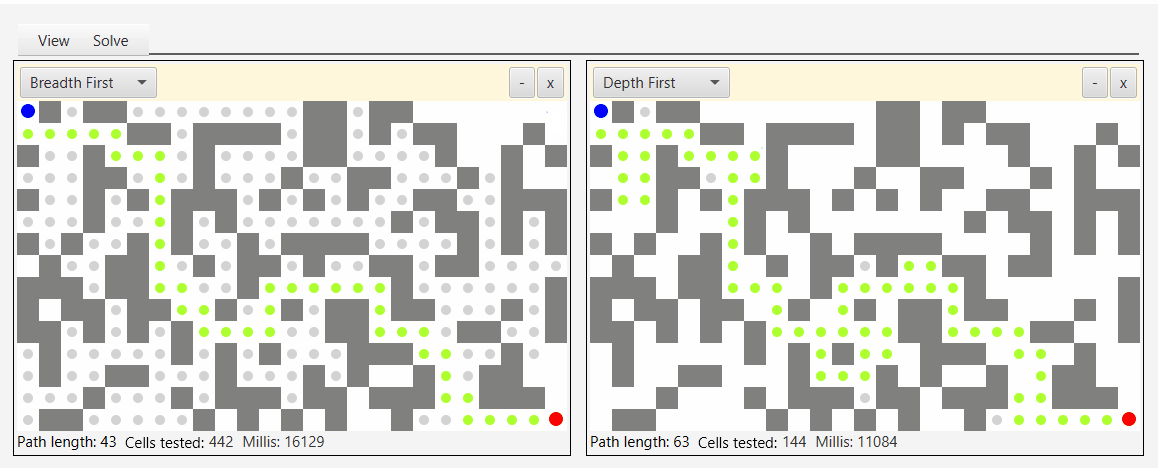
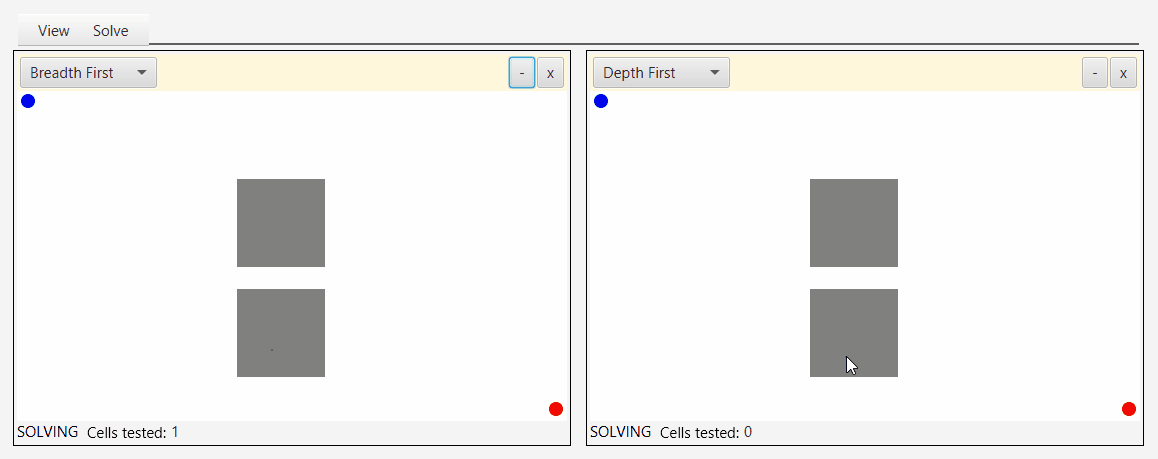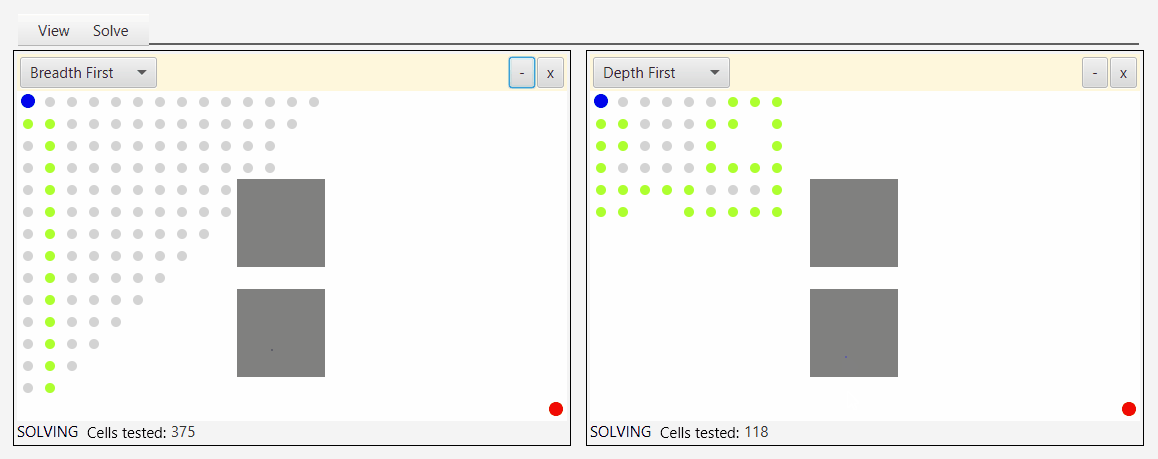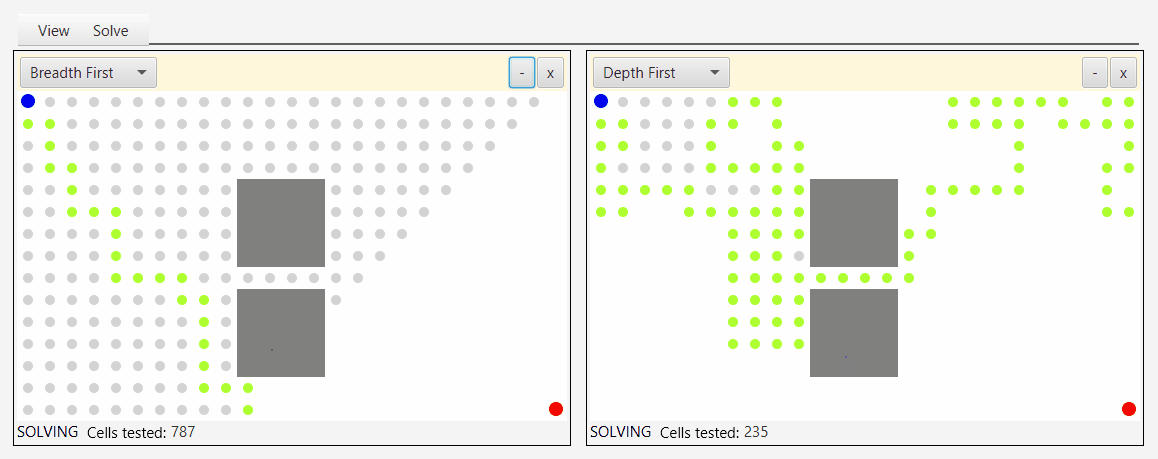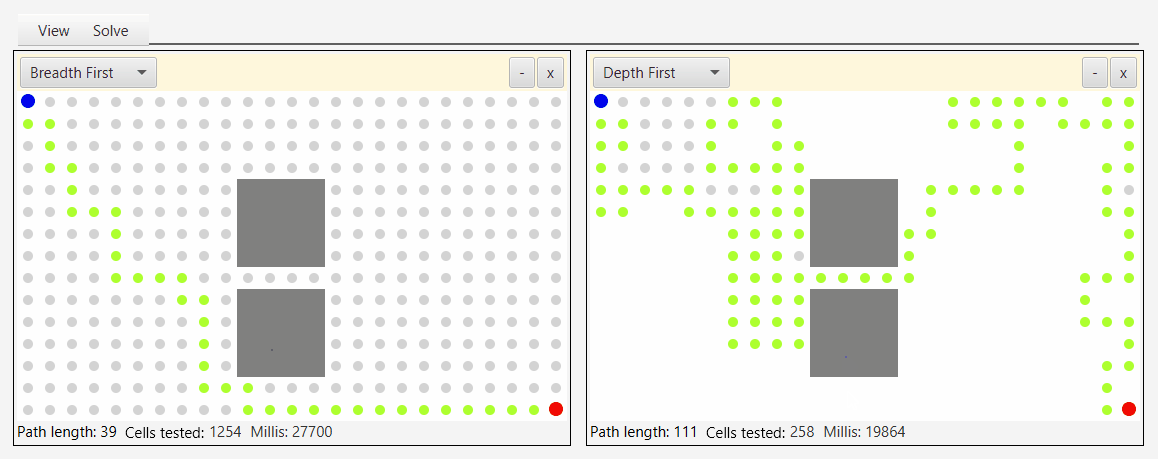
Вот снимок экрана инструмента, который я создал для демонстрации и тестирования алгоритмов обхода:

Глядя на серые точки, которые представляют исследуемые узлы, вы можете увидеть природу бфс, аналога наводнения водой.

Answer 2

Первый подход вовсе не DFS, по крайней мере, в каноническом определении алгоритма DFS. Это просто BFS, в которой кто-то заменил очередь на стек. Однако эта реализация достаточно хороша для "имитации" DFS в том смысле, что она обнаруживает вершины графа в DFS-подобном порядке. Его можно назвать "псевдо-DFS", если хотите, из-за порядка обнаружения, подобного DFS, но канонический алгоритм DFS намного больше этого.

Каноническая DFS не только следует за порядком обнаружения вершин первой глубины, но также производит определенный порядок "обнаружения", определенный порядок возврата (т. Е. Момент, когда "серая" вершина становится "черной" вершиной в классической номенклатуре Дейкстры). В первой реализации эта важная особенность канонической DFS отсутствует (или ее невозможно реализовать каким-либо разумным способом).

Между тем, второй подход является явно рекурсивной реализацией классического алгоритма DFS.

В любом случае, реальная DFS или псевдо-DFS, не существует "одного истинного порядка", в котором следует посещать вершины. Обе реализации могут быть созданы для создания одного и того же порядка посещения вершин. В вашем случае никто просто не удосужился это сделать. Разница в выводе обусловлена ​​тем фактом, что предыдущая реализация посещает соседей в обратном порядке - от последнего к первому. Все соседи сначала помещаются в стек, а затем выталкиваются один за другим в целях посещения. Поведение стека в LIFO - это то, что вызывает обращение. Между тем, последняя реализация посещает соседей в их прямом порядке - от первого до последнего.

Если вы замените цикл в последней реализации на

for (int i = neighbours.size() - 1; i >= 0; --i) 

Вы должны получить одинаковый порядок посещения (одинаковый вывод) в обеих реализациях.