Временные ряды из спектра

Question

У меня проблема с Сэмлом при преобразовании спектра во временные ряды. Я прочитал много статей, я думаю, что я применяю правильную процедуру, но я не получаю правильные результаты. Не могли бы вы помочь найти ошибку?

У меня есть временной ряд, как:

Когда я вычисляю спектр, я делаю: % количество точек nPoints=length(timeSeries);

%time interval
dt=time(2)-time(1);

%Fast Fourier transform
p=abs(fft(timeSeries))./(nPoints/2);

%power of positive frequencies
spectrum=p(1:(nPoints/2)).^2;

%frequency
dfFFT=1/tDur;
frequency=(1:nPoints)*dfFFT;
frequency=frequency(1:(nPoints)/2);

%plot spectrum
semilogy(frequency,spectrum); grid on;
xlabel('Frequency [Hz]');
ylabel('Power Spectrum [N*m]^2/[Hz]');
title('SPD load signal');

И я получаю:

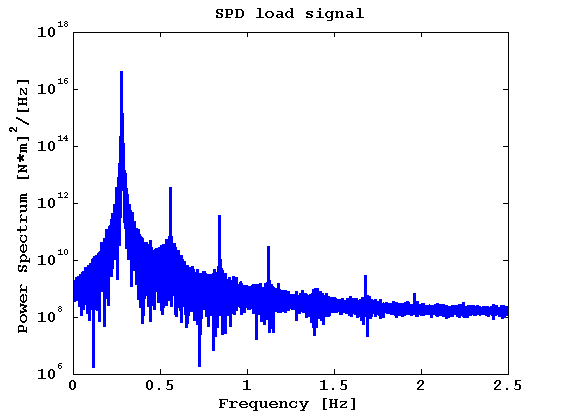
Я думаю, что спектр хорошо рассчитан. Однако теперь мне нужно вернуться и получить временные ряды из этого спектра, и я делаю:

df=frequency(2)-frequency(1);
ap = sqrt(2.*spectrum*df)';
%random number form -pi to pi    
epsilon=-pi + 2*pi*rand(1,length(ap));
%transform to time series
randomSeries=length(time).*real(ifft(pad(ap.*exp(epsilon.*i.*2.*pi),length(time))));
%Add the mean value
randomSeries=randomSeries+mean(timeSeries);

Тем не менее, сюжет выглядит так:

Где он на порядок ниже оригинальной серии. Любая рекомендация?

Answer 1

Здесь есть (по крайней мере) две вещи. Во-первых, вы отбрасываете информацию, а затем подставляете случайные числа для этой информации.

БПФ действительной последовательности представляет собой последовательность комплексных чисел, состоящую из действительной и мнимой частей. Преобразование этих чисел в полярную форму дает вам величину и фазовый угол. Вы захватываете часть величины с p=aps(fft(...)), но вы не захватываете фазовый угол (который будет включать в себя atan2(...)). Вы тогда составляете случайные числа (epsilon=...) и использовать их для замены исходных чисел при реконструкции временных рядов. Кроме того, поскольку БПФ реальной последовательности имеет определенную симметрию, замена случайных чисел на фазовый угол разрушает эту симметрию, что означает, что ОБПФ в общем случае будет уже не действительной последовательностью, а последовательностью комплексных чисел - и снова вы смотрите только на реальную часть IFFT, поэтому вы снова выбрасываете информацию. Если это аудиосигнал, результаты могут звучать как оригинал (или они могут быть совершенно другими), но форма сигнала определенно не будет соответствовать...

Вторая проблема заключается в том, что во многих реализациях ifft(fft(...)) масштабирует результат по количеству точек в сигнале. Есть несколько способов избежать этого, с разными результатами, но иногда более привлекательными в разных сценариях, в зависимости от того, что вы пытаетесь сделать. Вы можете масштабировать fft() результат, прежде чем сделать ifft()или масштабировать ifft() результат в конце, или в некоторых случаях, я даже видел, как оба масштабируются с коэффициентом sqrt(N) - выполнение этого дважды приводит к конечному результату масштабирования N, но это немного менее эффективно, так как вы делаете масштабирование дважды...