Z3 не может доказать эквивалентность между двумя простыми программами, использующими алгебры Клини с тестом, но Mathematica и Reduce способны

Question

Наша проблема заключается в том, чтобы показать, что

используя алгебры Клини с тестом.

В случае, когда значение b сохраняется p, мы имеем условие коммутативности bp = pb; и эквивалентность между двумя программами сводится к уравнению

В случае, когда значение b не сохраняется p, мы имеем условие коммутативности pc = cp; и эквивалентность между двумя программами сводится к уравнению

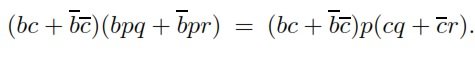
Я пытаюсь доказать первое уравнение, используя следующий код SMT-LIB

(declare-sort S)
(declare-fun sum (S S) S)
(declare-fun mult (S S) S)
(declare-fun neg (S) S)
(assert (forall ((x S) (y S) (z S)) (= (mult x (sum y z)) (sum (mult x y) (mult y z)))   ) )
(assert (forall ((x S) (y S) (z S)) (= (mult (sum y z) x) (sum (mult y x) (mult z x)))   ) )
(assert (forall ((x S) (y S) (z S)) (= (mult x (mult y z)) (mult (mult x y) z))    ))
(check-sat)
(push)
(declare-fun b () S)
(declare-fun p () S)
(declare-fun q () S)
(declare-fun r () S)
(assert (= (mult b p) (mult p b)) )
(check-sat)
(pop)

но я получаю timeout; то есть Z3 не может передать условие коммутативности bp = pb. Пожалуйста, запустите этот пример онлайн здесь.

Z3 не может доказать эти уравнения, но Mathematica и Reduce способны. Z3 не так мощен, как доказатель теорем. Ты согласен?

Answer 1

Первое уравнение доказано с использованием Z3 со следующим кодом SMT-LIB

(declare-sort S)
(declare-fun e () S)
(declare-fun O () S)
(declare-fun mult (S S) S)
(declare-fun sum  (S S) S)
(declare-fun leq (S S) Bool)
(declare-fun negation (S) S)
(declare-fun test (S) Bool)
(assert (forall ((x S) (y S))  (= (sum x y) (sum y x ))))
(assert (forall ((x S) (y S) (z S)) (= (sum (sum x y) z) (sum x (sum y z)))))
(assert (forall ((x S)) (= (sum O x)  x)))
(assert (forall ((x S)) (= (sum x x)  x)))
(assert (forall ((x S) (y S) (z S)) (= (mult (mult x y) z) (mult x (mult y z)))))
(assert (forall ((x S)) (= (mult e x)  x)))
(assert (forall ((x S)) (= (mult x e)  x)))
(assert (forall ((x S) (y S) (z S)) (= (mult x (sum y z) ) (sum   (mult x y) (mult x z)))))
(assert (forall ((x S) (y S) (z S)) (= (mult (sum x y) z ) (sum   (mult x z) (mult y z)))))
(assert (forall ((x S)) (= (mult x O)  O)))
(assert (forall ((x S)) (= (mult O x)  O)))
(assert (forall ((x S) (y S))  (= (leq x y) (= (sum x y) y))))
(assert (forall ((x S) (y S)) (=> (and (test x) (test y) )  (= (mult x y) (mult y x))) ) )
(assert (forall ((x S)) (=> (test x) (= (sum x (negation x)) e)  ))) 
(assert (forall ((x S)) (=> (test x) (= (mult x (negation x)) O)  ))) 
(check-sat)

(push)
;; bpq + b`pr = p(bq + b`r)
(declare-fun b () S)
(declare-fun p () S)
(declare-fun q () S)
(declare-fun r () S)
(assert (=> (test b) (= (mult p b) (mult b p))   )) 
(assert  (=> (test b) (= (mult p (negation b)) (mult (negation b) p)))) 
(check-sat)
(assert (not (=> (test b) (= (sum (mult b (mult p q)) (mult (negation b) (mult p r) )) 
                                                               (mult p (sum (mult b q) (mult (negation b) r)))))      ) ) 
(check-sat)
(pop)
(echo "Proved: bpq + b`pr = p(bq + b`r)")

Выход

sat
sat
unsat
Proved: bpq + b`pr = p(bq + b`r)

Пожалуйста, запустите это доказательство онлайн здесь

Answer 2

Второе уравнение косвенно доказывается с использованием Z3 со следующей процедурой

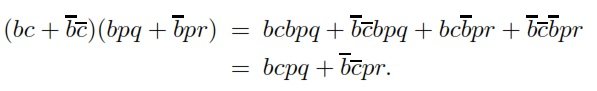
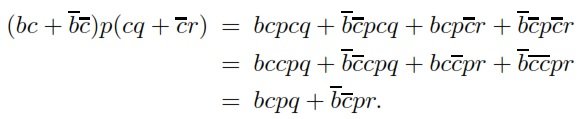
Эта косвенная процедура реализована с помощью следующего кода SMT-LIB

(declare-sort S)
(declare-fun e () S)
(declare-fun O () S)
(declare-fun mult (S S) S)
(declare-fun sum  (S S) S)
(declare-fun leq (S S) Bool)
(declare-fun negation (S) S)
(declare-fun test (S) Bool)
(assert (forall ((x S) (y S))  (= (sum x y) (sum y x ))))
(assert (forall ((x S) (y S) (z S)) (= (sum (sum x y) z) (sum x (sum y z)))))
(assert (forall ((x S)) (= (sum O x)  x)))
(assert (forall ((x S)) (= (sum x x)  x)))
(assert (forall ((x S) (y S) (z S)) (= (mult (mult x y) z) (mult x (mult y z)))))
(assert (forall ((x S)) (= (mult e x)  x)))
(assert (forall ((x S)) (= (mult x e)  x)))
(assert (forall ((x S) (y S) (z S)) (= (mult x (sum y z) ) (sum   (mult x y) (mult x z)))))
(assert (forall ((x S) (y S) (z S)) (= (mult (sum x y) z ) (sum   (mult x z) (mult y z)))))
(assert (forall ((x S)) (= (mult x O)  O)))
(assert (forall ((x S)) (= (mult O x)  O)))
(assert (forall ((x S) (y S))  (= (leq x y) (= (sum x y) y))))
(assert (forall ((x S) (y S)) (=> (and (test x) (test y) )  (= (mult x y) (mult y x))) ) )
(assert (forall ((x S)) (=> (test x) (= (sum x (negation x)) e)  ))) 
(assert (forall ((x S)) (=> (test x) (= (mult x (negation x)) O)  ))) 
(assert (forall ((x S)) (=> (test x) (test (negation x))   )) )
(assert (forall ((x S)) (=> (test x) (= (mult x x) x)   )) )
(check-sat)

    (push)



(declare-fun c () S)
(declare-fun b () S)
(declare-fun p () S)
(declare-fun q () S)
(declare-fun r () S)
    (check-sat)
    (assert (not (=> (and (test b) (test c))  
                                                       (= (mult (sum (mult b c) (mult (negation b) (negation c))) 
                                                                 (sum (mult b (mult p q)) (mult (negation b) (mult p r) ) ))
                                                           (sum (mult b (mult c (mult p q))) 
                                                                (mult (negation b) (mult (negation c) (mult p r) ) ) )))   ) )

    (check-sat)
    (pop)
    (echo "Proved: part 1")

    (push)
    ;;
    (assert (=> (test c) (= (mult p c) (mult c p))   )) 
    (assert  (=> (test c) (= (mult p (negation c)) (mult (negation c) p)))) 
    (check-sat)
    (assert (not (=> (test c) 
                     (= (mult (sum (mult b c) (mult (negation b) (negation c))) 
                              (mult p (sum (mult c q) (mult (negation c) r)))) 
                        (sum (mult b (mult c (mult p q))) 
                             (mult (negation b) (mult (negation c) (mult p r) ) )  )))   ) )
    (check-sat)
    (pop)
    (echo "Proved: part 2")

и соответствующий вывод

sat
sat
unsat
Proved: part 1
sat
unsat
Proved: part 2

Этот вывод получается локально. Когда код выполняется онлайн, вывод

sat 
sat 
unsat 
Proved: part 1 
sat
timeout

Пожалуйста, запустите этот пример онлайн здесь

Z3 не может доказать второе уравнение напрямую, но Mathematica и Reduce anable.