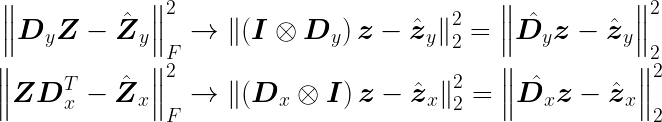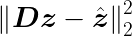Решение наименьших квадратов для матрицы вместо вектора

Question

Задача состоит в том, чтобы найти Z таким, чтобы эпсилон (E) (уравнение 21) был минимизирован.

Z - это матрица MxN, которую мы должны найти. Zx и Zy также являются матрицами MxN, которые также уже известны. Dx и Dy - это матрицы NxN, которые проводят численное дифференцирование (см. Матрицу, обведенную красным на фотографии), поэтому они также являются известными матрицами. F обозначает "норму Фобрениуса" или "исходную норму".

Как решить эту проблему? Я знаю, как решить задачу наименьших квадратов для вектора, но теперь он в матричной форме, и я застреваю.
Спасибо

Answer 1

Используйте это

          normF(A*Z-B)^2=trace((A*Z-B).T*(A*Z-B))

так что для производной по направлению в направлении dZ вы получаете

          2*trace((A*dZ).T*(A*Z-B))=dotF(dZ,A.T*(A*Z-B))

Обычно это интерпретируется как производнаяA.T*(A*Z-B).

В другом члене вы получаете аналогично:

          normF(Z*A.T-B.T)^2 = trace((A*Z.T-B)*(Z*A.T-B.T))

с производной по направлению

          2*trace(A*dZ.T*(Z*A.T-B.T))=dotF(dZ,(Z*A.T-B.T)*A)

Добавлениеxиyк именам матриц дает в сумме производную

          2*Z*(Ax.T*Ax) + 2*(Ay.T*Ay)*Z - 2*Bx.T*Ax - 2*Ay.T*By

уравнение вида

          Z*Qx + Qy*Z = C

Теперь возьмем диагонализацииQ=U*D*U.Tс ортогональнымUи диагональD, умножить влево наUy.T, прямо мимоUxполучить

      (Uy.T*Z*Ux)*Dx + Dy*(Uy.T*Z*U) = (Uy.T*C*Ux)

и можно прочитать алгоритм решения. Поэлементное вычисление(Uy.T*Z*Ux), затем получитьZпутем матричного умножения.

Answer 2

Хитрость здесь заключается в использовании продукта Кронекера :

$$ \begin{align*} {\left| \boldsymbol{D} {y} \boldsymbol{Z} - \hat{\boldsymbol{Z}} {y} \right|} {F}^{2} & \rightarrow {\left| \left( \boldsymbol{I} \otimes \boldsymbol{D} {y} \right) \boldsymbol{z} - \hat{\boldsymbol{z}} {y} \right|} {2}^{2} = {\ влево| \hat{\boldsymbol{D} {y}} \boldsymbol{z} - \hat{\boldsymbol{z}} {y} \right|} {2}^{2} \ {\left| \boldsymbol{Z} \boldsymbol{D} {x}^{T} - \hat{\boldsymbol{Z}} {x} \right|} {F}^{2} & \rightarrow {\left| \left( \boldsymbol{D} {x} \otimes \boldsymbol{I} \right) \boldsymbol{z} - \hat{\boldsymbol{z}} {x} \right|} {2}^{2} = {\ влево| \hat{\boldsymbol{D} {x}} \boldsymbol{z} - \hat{\boldsymbol{z}} {x} \right|} {2}^{2} \end{align*} $$

Что эквивалентно решению:

$$ {\ влево| \boldsymbol{D} \boldsymbol{z} - \hat{\boldsymbol{z}} \right|}_{2}^{2} $$

Где матрица $\boldsymbol{D}$ получается путем укладки матриц по горизонтали, а $\hat{\boldsymbol{z}$ — путем укладки по вертикали.

Реализация должна использовать преимущество разреженности соответствующих матриц, чтобы все вычисления были столь же эффективны, как и исходная формулировка.