Как убрать дефекты выпуклости на площади Судоку?

Question

Я занимался веселым проектом: Решением судоку из входного изображения с использованием OpenCV (как в Google Goggles и т. Д.). И я выполнил задание, но в конце обнаружил небольшую проблему, ради которой я пришел сюда.

Я занимался программированием с использованием Python API OpenCV 2.3.1.

Ниже то, что я сделал:

1. Прочитайте изображение
2. Найти контуры
3. Выберите тот, который имеет максимальную площадь, (а также несколько эквивалентен квадрату).

4. Найдите угловые точки.

   например, дано ниже:

   

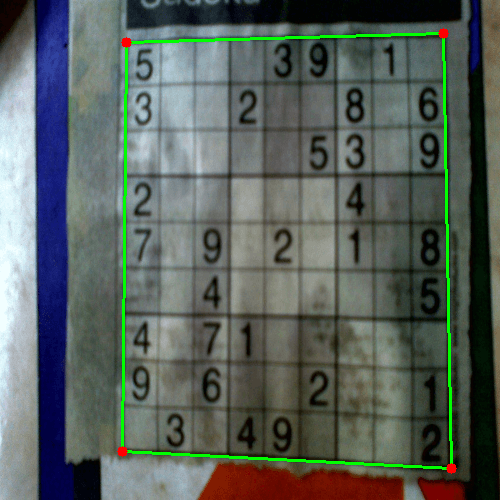
   (Обратите внимание, что зеленая линия правильно совпадает с истинной границей судоку, поэтому судоку можно правильно деформировать. Проверьте следующее изображение)

5. деформировать изображение в идеальный квадрат

   например, изображение:

   

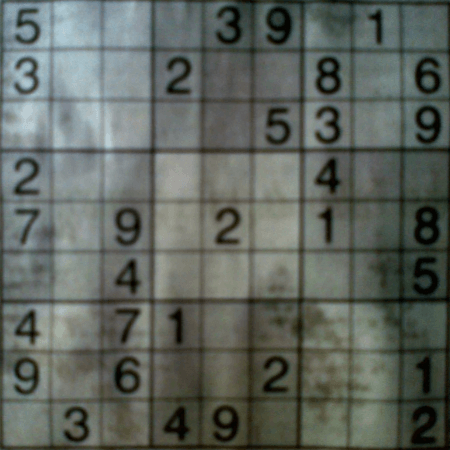
6. Выполнить OCR (для которого я использовал метод, который я дал в Простом распознавании цифр OCR в OpenCV-Python)

И метод работал хорошо.

Проблема:

Проверьте это изображение.

Выполнение шага 4 на этом изображении дает следующий результат:

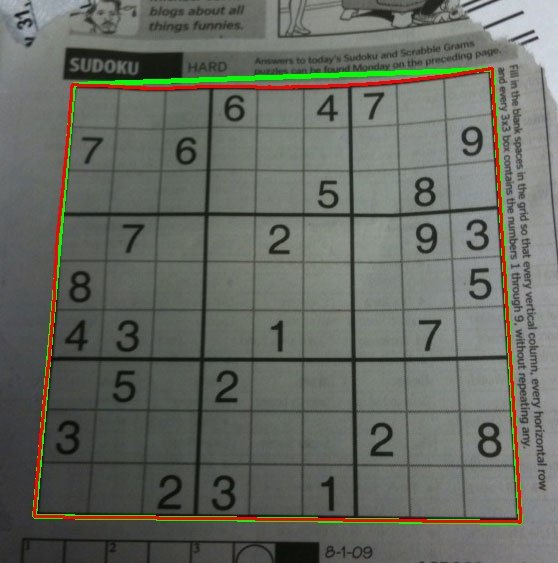
Красная линия - это оригинальный контур, который является истинным контуром границы судоку.

Нарисованная зеленая линия представляет собой приблизительный контур, который будет контуром искривленного изображения.

Что, конечно, есть разница между зеленой линией и красной линией на верхнем краю судоку. Таким образом, пока я не искажаю исходную границу Судоку.

Мой вопрос:

Как можно деформировать изображение на правильной границе судоку, то есть на красной линии ИЛИ как убрать разницу между красной линией и зеленой линией? Есть ли способ для этого в OpenCV?

Answer 1

У меня есть решение, которое работает, но вам придется самостоятельно перевести его на OpenCV. Это написано в Mathematica.

Первый шаг - настроить яркость изображения, разделив каждый пиксель в результате операции закрытия:

src = ColorConvert[Import["http://davemark.com/images/sudoku.jpg"], "Grayscale"];
white = Closing[src, DiskMatrix[5]];
srcAdjusted = Image[ImageData[src]/ImageData[white]]

Следующий шаг - найти область судоку, чтобы я мог игнорировать (маскировать) фон. Для этого я использую анализ связанных компонентов и выбираю компонент с наибольшей выпуклой областью:

components = 
  ComponentMeasurements[
    ColorNegate@Binarize[srcAdjusted], {"ConvexArea", "Mask"}][[All, 
    2]];
largestComponent = Image[SortBy[components, First][[-1, 2]]]

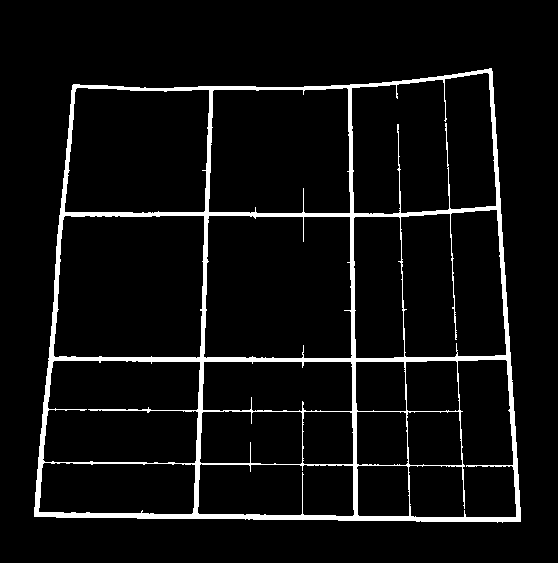
Заполняя это изображение, я получаю маску для сетки судоку:

mask = FillingTransform[largestComponent]

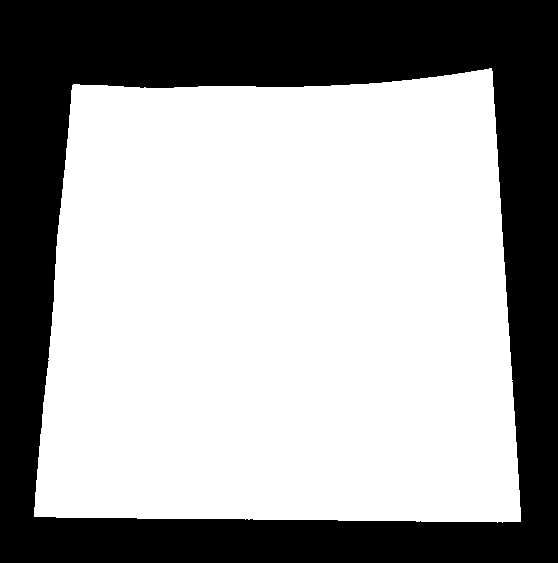
Теперь я могу использовать производный фильтр 2-го порядка, чтобы найти вертикальные и горизонтальные линии в двух отдельных изображениях:

lY = ImageMultiply[MorphologicalBinarize[GaussianFilter[srcAdjusted, 3, {2, 0}], {0.02, 0.05}], mask];
lX = ImageMultiply[MorphologicalBinarize[GaussianFilter[srcAdjusted, 3, {0, 2}], {0.02, 0.05}], mask];

Я снова использую анализ связанных компонентов, чтобы извлечь линии сетки из этих изображений. Линии сетки намного длиннее цифр, поэтому я могу использовать длину штангенциркуля для выбора только компонентов, соединенных линиями сетки. Сортируя их по положению, я получаю маски 2х10 для каждой вертикальной / горизонтальной линии сетки на изображении:

verticalGridLineMasks = 
  SortBy[ComponentMeasurements[
      lX, {"CaliperLength", "Centroid", "Mask"}, # > 100 &][[All, 
      2]], #[[2, 1]] &][[All, 3]];
horizontalGridLineMasks = 
  SortBy[ComponentMeasurements[
      lY, {"CaliperLength", "Centroid", "Mask"}, # > 100 &][[All, 
      2]], #[[2, 2]] &][[All, 3]];

Затем я беру каждую пару вертикальных / горизонтальных линий сетки, расширяю их, вычисляю попиксельное пересечение и вычисляю центр результата. Эти точки являются пересечениями линий сетки:

centerOfGravity[l_] := 
 ComponentMeasurements[Image[l], "Centroid"][[1, 2]]
gridCenters = 
  Table[centerOfGravity[
    ImageData[Dilation[Image[h], DiskMatrix[2]]]*
     ImageData[Dilation[Image[v], DiskMatrix[2]]]], {h, 
    horizontalGridLineMasks}, {v, verticalGridLineMasks}];

Последний шаг - определить две функции интерполяции для отображения X/Y через эти точки и преобразовать изображение с помощью этих функций:

fnX = ListInterpolation[gridCenters[[All, All, 1]]];
fnY = ListInterpolation[gridCenters[[All, All, 2]]];
transformed = 
 ImageTransformation[
  srcAdjusted, {fnX @@ Reverse[#], fnY @@ Reverse[#]} &, {9*50, 9*50},
   PlotRange -> {{1, 10}, {1, 10}}, DataRange -> Full]

Все операции являются основной функцией обработки изображений, поэтому это должно быть возможно и в OpenCV. Преобразование изображений на основе сплайнов может быть сложнее, но я не думаю, что оно вам действительно нужно. Возможно, использование трансформации перспективы, которую вы используете сейчас в каждой отдельной ячейке, даст достаточно хорошие результаты.

Answer 2

Ответ Ники решил мою проблему, но он был в Mathematica. Так что я подумал, что мне следует дать здесь адаптацию OpenCV. Но после реализации я увидел, что код OpenCV намного больше, чем код mathematica nikie. Кроме того, я не смог найти метод интерполяции, сделанный nikie в OpenCV (хотя это можно сделать с помощью scipy, я скажу это, когда придет время).

1. Предварительная обработка изображения (операция закрытия)

import cv2
import numpy as np

img = cv2.imread('dave.jpg')
img = cv2.GaussianBlur(img,(5,5),0)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
mask = np.zeros((gray.shape),np.uint8)
kernel1 = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(11,11))

close = cv2.morphologyEx(gray,cv2.MORPH_CLOSE,kernel1)
div = np.float32(gray)/(close)
res = np.uint8(cv2.normalize(div,div,0,255,cv2.NORM_MINMAX))
res2 = cv2.cvtColor(res,cv2.COLOR_GRAY2BGR)

Результат:

2. Найти площадь Судоку и создать изображение маски

thresh = cv2.adaptiveThreshold(res,255,0,1,19,2)
contour,hier = cv2.findContours(thresh,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)

max_area = 0
best_cnt = None
for cnt in contour:
    area = cv2.contourArea(cnt)
    if area > 1000:
        if area > max_area:
            max_area = area
            best_cnt = cnt

cv2.drawContours(mask,[best_cnt],0,255,-1)
cv2.drawContours(mask,[best_cnt],0,0,2)

res = cv2.bitwise_and(res,mask)

Результат:

3. Нахождение вертикальных линий

kernelx = cv2.getStructuringElement(cv2.MORPH_RECT,(2,10))

dx = cv2.Sobel(res,cv2.CV_16S,1,0)
dx = cv2.convertScaleAbs(dx)
cv2.normalize(dx,dx,0,255,cv2.NORM_MINMAX)
ret,close = cv2.threshold(dx,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
close = cv2.morphologyEx(close,cv2.MORPH_DILATE,kernelx,iterations = 1)

contour, hier = cv2.findContours(close,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)
for cnt in contour:
    x,y,w,h = cv2.boundingRect(cnt)
    if h/w > 5:
        cv2.drawContours(close,[cnt],0,255,-1)
    else:
        cv2.drawContours(close,[cnt],0,0,-1)
close = cv2.morphologyEx(close,cv2.MORPH_CLOSE,None,iterations = 2)
closex = close.copy()

Результат:

4. Нахождение горизонтальных линий

kernely = cv2.getStructuringElement(cv2.MORPH_RECT,(10,2))
dy = cv2.Sobel(res,cv2.CV_16S,0,2)
dy = cv2.convertScaleAbs(dy)
cv2.normalize(dy,dy,0,255,cv2.NORM_MINMAX)
ret,close = cv2.threshold(dy,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
close = cv2.morphologyEx(close,cv2.MORPH_DILATE,kernely)

contour, hier = cv2.findContours(close,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)
for cnt in contour:
    x,y,w,h = cv2.boundingRect(cnt)
    if w/h > 5:
        cv2.drawContours(close,[cnt],0,255,-1)
    else:
        cv2.drawContours(close,[cnt],0,0,-1)

close = cv2.morphologyEx(close,cv2.MORPH_DILATE,None,iterations = 2)
closey = close.copy()

Результат:

Конечно, этот не так хорош.

5. Нахождение точек сетки

res = cv2.bitwise_and(closex,closey)

Результат:

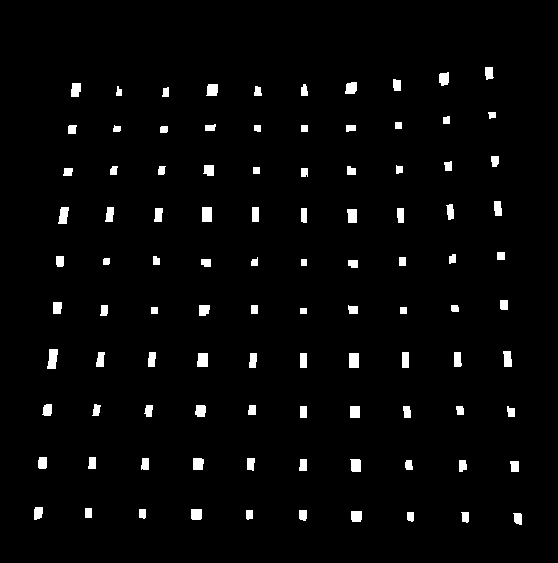
6. Исправление дефектов

Здесь Ники делает какую-то интерполяцию, о которой я мало что знаю. И я не мог найти соответствующую функцию для этого OpenCV. (может быть, это там, я не знаю).

Проверьте этот SOF, который объясняет, как сделать это с помощью SciPy, который я не хочу использовать: Преобразование изображений в OpenCV

Итак, здесь я взял 4 угла каждого квадрата и применил перспективу деформации к каждому.

Для этого сначала мы найдем центроиды.

contour, hier = cv2.findContours(res,cv2.RETR_LIST,cv2.CHAIN_APPROX_SIMPLE)
centroids = []
for cnt in contour:
    mom = cv2.moments(cnt)
    (x,y) = int(mom['m10']/mom['m00']), int(mom['m01']/mom['m00'])
    cv2.circle(img,(x,y),4,(0,255,0),-1)
    centroids.append((x,y))

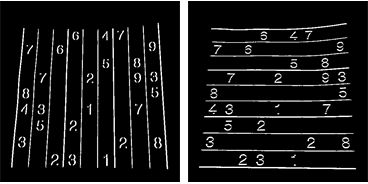
Но получившиеся центроиды не будут отсортированы. Проверьте ниже изображение, чтобы увидеть их порядок:

Поэтому мы сортируем их слева направо, сверху вниз.

centroids = np.array(centroids,dtype = np.float32)
c = centroids.reshape((100,2))
c2 = c[np.argsort(c[:,1])]

b = np.vstack([c2[i*10:(i+1)*10][np.argsort(c2[i*10:(i+1)*10,0])] for i in xrange(10)])
bm = b.reshape((10,10,2))

Теперь смотрите ниже их порядок:

Наконец мы применяем преобразование и создаем новое изображение размером 450x450.

output = np.zeros((450,450,3),np.uint8)
for i,j in enumerate(b):
    ri = i/10
    ci = i%10
    if ci != 9 and ri!=9:
        src = bm[ri:ri+2, ci:ci+2 , :].reshape((4,2))
        dst = np.array( [ [ci*50,ri*50],[(ci+1)*50-1,ri*50],[ci*50,(ri+1)*50-1],[(ci+1)*50-1,(ri+1)*50-1] ], np.float32)
        retval = cv2.getPerspectiveTransform(src,dst)
        warp = cv2.warpPerspective(res2,retval,(450,450))
        output[ri*50:(ri+1)*50-1 , ci*50:(ci+1)*50-1] = warp[ri*50:(ri+1)*50-1 , ci*50:(ci+1)*50-1].copy()

Результат:

Результат почти такой же, как у nikie, но длина кода велика. Может быть, есть лучшие методы, но до тех пор это работает хорошо.

С уважением ARK.

Answer 3

Вы можете попробовать использовать какое-то сеточное моделирование произвольной деформации. А поскольку судоку уже является сеткой, это не должно быть слишком сложно.

Таким образом, вы можете попытаться определить границы каждого субрегиона 3х3, а затем деформировать каждый регион в отдельности. Если обнаружение пройдет успешно, это даст вам лучшее приближение.

Answer 4

Я подумал, что это отличный пост и отличное решение от ARK; очень хорошо изложено и объяснено.

Я работал над аналогичной проблемой и построил все. Были внесены некоторые изменения (например, xrange to range, аргументы в cv2.findContours), но это должно работать из коробки (Python 3.5, Anaconda).

Это компиляция вышеперечисленных элементов с добавлением некоторого недостающего кода (например, маркировка точек).

'''

https://stackru.com/questions/10196198/how-to-remove-convexity-defects-in-a-sudoku-square

'''

import cv2
import numpy as np

img = cv2.imread('test.png')

winname="raw image"
cv2.namedWindow(winname)
cv2.imshow(winname, img)
cv2.moveWindow(winname, 100,100)


img = cv2.GaussianBlur(img,(5,5),0)

winname="blurred"
cv2.namedWindow(winname)
cv2.imshow(winname, img)
cv2.moveWindow(winname, 100,150)

gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
mask = np.zeros((gray.shape),np.uint8)
kernel1 = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(11,11))

winname="gray"
cv2.namedWindow(winname)
cv2.imshow(winname, gray)
cv2.moveWindow(winname, 100,200)

close = cv2.morphologyEx(gray,cv2.MORPH_CLOSE,kernel1)
div = np.float32(gray)/(close)
res = np.uint8(cv2.normalize(div,div,0,255,cv2.NORM_MINMAX))
res2 = cv2.cvtColor(res,cv2.COLOR_GRAY2BGR)

winname="res2"
cv2.namedWindow(winname)
cv2.imshow(winname, res2)
cv2.moveWindow(winname, 100,250)

 #find elements
thresh = cv2.adaptiveThreshold(res,255,0,1,19,2)
img_c, contour,hier = cv2.findContours(thresh,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)

max_area = 0
best_cnt = None
for cnt in contour:
    area = cv2.contourArea(cnt)
    if area > 1000:
        if area > max_area:
            max_area = area
            best_cnt = cnt

cv2.drawContours(mask,[best_cnt],0,255,-1)
cv2.drawContours(mask,[best_cnt],0,0,2)

res = cv2.bitwise_and(res,mask)

winname="puzzle only"
cv2.namedWindow(winname)
cv2.imshow(winname, res)
cv2.moveWindow(winname, 100,300)

# vertical lines
kernelx = cv2.getStructuringElement(cv2.MORPH_RECT,(2,10))

dx = cv2.Sobel(res,cv2.CV_16S,1,0)
dx = cv2.convertScaleAbs(dx)
cv2.normalize(dx,dx,0,255,cv2.NORM_MINMAX)
ret,close = cv2.threshold(dx,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
close = cv2.morphologyEx(close,cv2.MORPH_DILATE,kernelx,iterations = 1)

img_d, contour, hier = cv2.findContours(close,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)
for cnt in contour:
    x,y,w,h = cv2.boundingRect(cnt)
    if h/w > 5:
        cv2.drawContours(close,[cnt],0,255,-1)
    else:
        cv2.drawContours(close,[cnt],0,0,-1)
close = cv2.morphologyEx(close,cv2.MORPH_CLOSE,None,iterations = 2)
closex = close.copy()

winname="vertical lines"
cv2.namedWindow(winname)
cv2.imshow(winname, img_d)
cv2.moveWindow(winname, 100,350)

# find horizontal lines
kernely = cv2.getStructuringElement(cv2.MORPH_RECT,(10,2))
dy = cv2.Sobel(res,cv2.CV_16S,0,2)
dy = cv2.convertScaleAbs(dy)
cv2.normalize(dy,dy,0,255,cv2.NORM_MINMAX)
ret,close = cv2.threshold(dy,0,255,cv2.THRESH_BINARY+cv2.THRESH_OTSU)
close = cv2.morphologyEx(close,cv2.MORPH_DILATE,kernely)

img_e, contour, hier = cv2.findContours(close,cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)

for cnt in contour:
    x,y,w,h = cv2.boundingRect(cnt)
    if w/h > 5:
        cv2.drawContours(close,[cnt],0,255,-1)
    else:
        cv2.drawContours(close,[cnt],0,0,-1)

close = cv2.morphologyEx(close,cv2.MORPH_DILATE,None,iterations = 2)
closey = close.copy()

winname="horizontal lines"
cv2.namedWindow(winname)
cv2.imshow(winname, img_e)
cv2.moveWindow(winname, 100,400)


# intersection of these two gives dots
res = cv2.bitwise_and(closex,closey)

winname="intersections"
cv2.namedWindow(winname)
cv2.imshow(winname, res)
cv2.moveWindow(winname, 100,450)

# text blue
textcolor=(0,255,0)
# points green
pointcolor=(255,0,0)

# find centroids and sort
img_f, contour, hier = cv2.findContours(res,cv2.RETR_LIST,cv2.CHAIN_APPROX_SIMPLE)
centroids = []
for cnt in contour:
    mom = cv2.moments(cnt)
    (x,y) = int(mom['m10']/mom['m00']), int(mom['m01']/mom['m00'])
    cv2.circle(img,(x,y),4,(0,255,0),-1)
    centroids.append((x,y))

# sorting
centroids = np.array(centroids,dtype = np.float32)
c = centroids.reshape((100,2))
c2 = c[np.argsort(c[:,1])]

b = np.vstack([c2[i*10:(i+1)*10][np.argsort(c2[i*10:(i+1)*10,0])] for i in range(10)])
bm = b.reshape((10,10,2))

# make copy
labeled_in_order=res2.copy()

for index, pt in enumerate(b):
    cv2.putText(labeled_in_order,str(index),tuple(pt),cv2.FONT_HERSHEY_DUPLEX, 0.75, textcolor)
    cv2.circle(labeled_in_order, tuple(pt), 5, pointcolor)

winname="labeled in order"
cv2.namedWindow(winname)
cv2.imshow(winname, labeled_in_order)
cv2.moveWindow(winname, 100,500)

# create final

output = np.zeros((450,450,3),np.uint8)
for i,j in enumerate(b):
    ri = int(i/10) # row index
    ci = i%10 # column index
    if ci != 9 and ri!=9:
        src = bm[ri:ri+2, ci:ci+2 , :].reshape((4,2))
        dst = np.array( [ [ci*50,ri*50],[(ci+1)*50-1,ri*50],[ci*50,(ri+1)*50-1],[(ci+1)*50-1,(ri+1)*50-1] ], np.float32)
        retval = cv2.getPerspectiveTransform(src,dst)
        warp = cv2.warpPerspective(res2,retval,(450,450))
        output[ri*50:(ri+1)*50-1 , ci*50:(ci+1)*50-1] = warp[ri*50:(ri+1)*50-1 , ci*50:(ci+1)*50-1].copy()

winname="final"
cv2.namedWindow(winname)
cv2.imshow(winname, output)
cv2.moveWindow(winname, 600,100)

cv2.waitKey(0)
cv2.destroyAllWindows()

Answer 5

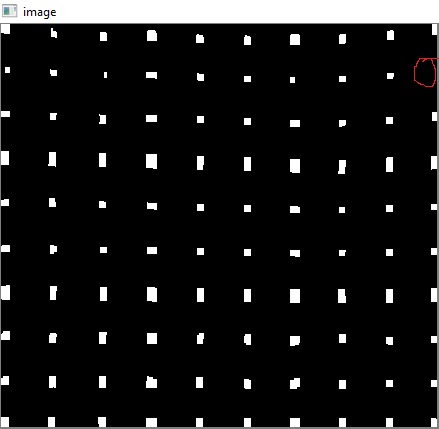
Для удаления незапятнанных углов я применил гамма-коррекцию со значением гаммы 0,8.

Красный круг нарисован, чтобы показать недостающий угол.

Код является:

gamma = 0.8
invGamma = 1/gamma
table = np.array([((i / 255.0) ** invGamma) * 255
                  for i in np.arange(0, 256)]).astype("uint8")
cv2.LUT(img, table, img)

Это в дополнение к ответу Абида Рахмана, если отсутствуют некоторые угловые точки.

Answer 6

Я хочу добавить, что описанный выше метод работает только в том случае, если доска судоку стоит прямо, в противном случае проверка соотношения высоты / ширины (или наоборот), скорее всего, провалится, и вы не сможете обнаружить края судоку. (Я также хочу добавить, что если линии, которые не перпендикулярны границам изображения, операции sobel (dx и dy) будут по-прежнему работать, так как линии будут по-прежнему иметь края относительно обеих осей.)

Чтобы иметь возможность обнаруживать прямые линии, вы должны работать с контурным или пиксельным анализом, таким как contourArea / boundingRectArea, верхняя левая и нижняя правая точки...

Изменить: мне удалось проверить, образует ли набор контуров линию или нет, применив линейную регрессию и проверив ошибку. Однако линейная регрессия выполняется плохо, когда наклон линии слишком велик (т. Е. >1000) или очень близок к 0. Поэтому применение вышеуказанного критерия отношения (в ответе с наибольшим количеством голосов) перед линейной регрессией логично и сработало для меня.