OpenCV projectPoints(): несовместимая ковариация / стандартное отклонение предполагаемых поз

Question

Я использую OpenCV в алгоритме оценки позы, где я также пытаюсь получить оценку неопределенности оцениваемой позы. Моя оценка позы выполняется с помощью 3D-2D соответствий и алгоритма PNP. Чтобы добиться оценки неопределенности, я пытаюсь использовать функцию projectPoints() для перепроецирования трехмерных точек обратно на плоскость изображения и использовать внутренне вычисленную матрицу Якоби для получения ковариации.

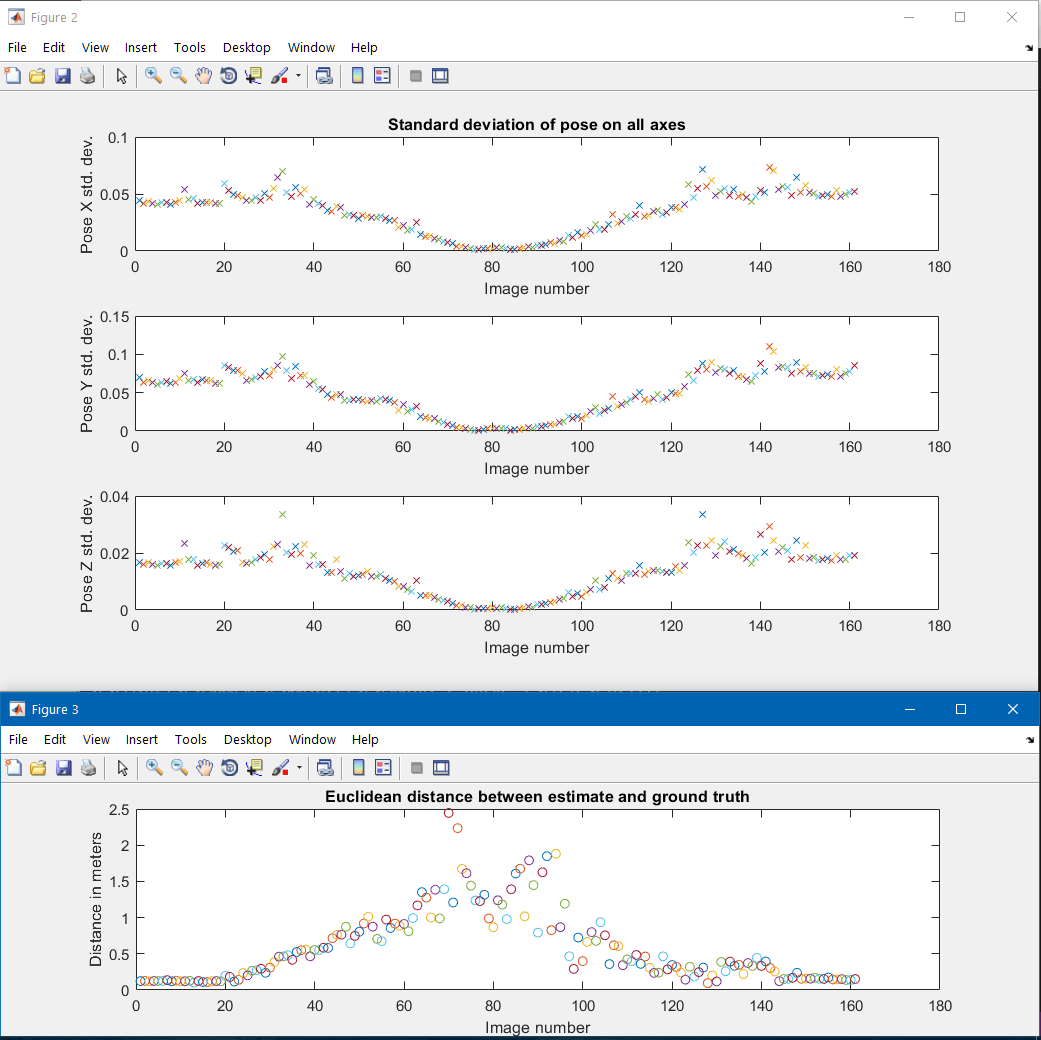
Моя функция "карта" содержит плоский набор трехмерных точек. Траектория моей камеры проста: я начинаю близко к объектам, двигаюсь назад и, таким образом, далеко от объектов, а затем снова ближе, пока не достигну начальной точки. Я использую 3D-симулятор (Unreal Engine) для получения этих изображений, и у меня есть правильные характеристики для камеры (и она имеет нулевые искажения). Проблема, которую я вижу, состоит в том, что ковариация и последующее стандартное отклонение (для перевода), оцененные с помощью projectPoints(), не коррелируют с фактической ошибкой положения. По мере того, как я отдаляюсь дальше, как и должно быть, оценка становится хуже, и позы ошибочны, но стандартное отклонение уменьшается. Я прилагаю график ошибки расстояния предполагаемой позы и, соответственно, оцененного стандартного отклонения, и они имеют противоположные профили. Код, в котором я пытаюсь вычислить это стандартное отклонение, выглядит следующим образом.

cv::Mat rvec, J;
cv::eigen2cv(pose.rotation(), rvec);
cv::Mat tvec = cv::Mat(1, 3, CV_32FC1, cv::Scalar::all(0));

tvec.at<float>(0, 0) = pose.center()[0];
tvec.at<float>(0, 1) = pose.center()[1];
tvec.at<float>(0, 2) = pose.center()[2];

cv::Mat p;
cv::projectPoints(objectPoints, rvec, tvec, K, dist, p, J);

std::vector <cv::Point2f> reprojected;

for (int i = 0; i < p.rows; i++) {
    reprojected.push_back(cv::Point2f(p.at<double>(i, 0), p.at<double>(i, 1)));
}
cv::Mat Sigma = cv::Mat(J.t() * J, cv::Rect(0, 0, 6, 6)).inv();
cv::Mat std_dev;
sqrt(Sigma.diag(), std_dev);

График ошибки расстояния в оценке относительно истинности земли; а также расчетное стандартное отклонение:

В чем может быть проблема здесь? Я понимаю, что якобиан между изменением позы и изменением ошибки репроекции не будет полностью кодировать ошибки позиционирования (например, небольшое изменение Z на большом расстоянии от характерных точек не сильно изменит ошибку репроекции), но Как мне получить достаточно надежные оценки качества моего решения при оценке поз?