Как расширить линию 2 PolyFit с любой стороны, чтобы пересечь и получить комбинированную линию подгонки

Question

Как расширить линию 2 PolyFit с любой стороны, чтобы пересечь и получить комбинированную линию подгонки

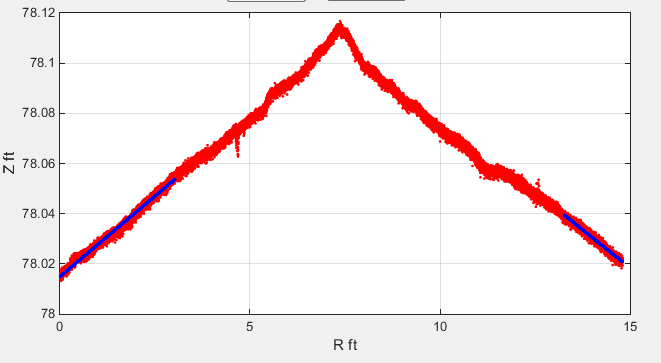
Я пытаюсь получить комбинированную линию подгонки, сделанную из двух линейных полифитов с обеих сторон (должна пересекаться), вот изображение линий подгонки:

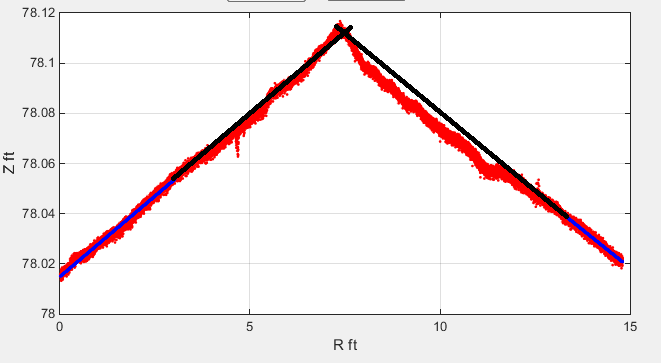
Я пытаюсь пересечь две подходящие (синие) линии и создать комбинированную линию соответствия, как показано на рисунке ниже:

Обратите внимание, что гребень может случиться где угодно, поэтому я не могу предположить, что он находится в центре.

Вот код, который создает первый график:

xdatPart1 = R;
zdatPart1 = z;

n = 3000;
ln = length(R);

[sX,In] = sort(R,1);

sZ = z(In);       

xdatP1 = sX(1:n,1);
zdatP1 = sZ(1:n,1);

n2 = ln - 3000;

xdatP2 = sX(n2:ln,1);
zdatP2 = sZ(n2:ln,1);

pp1 = polyfit(xdatP1,zdatP1,1);
pp2 = polyfit(xdatP2,zdatP2,1);

ff1 = polyval(pp1,xdatP1);
ff2 = polyval(pp2,xdatP2);

xDat = [xdatPart1];
zDat = [zdatPart1];

axes(handles.axes2);
cla(handles.axes2);
plot(xdatPart1,zdatPart1,'.r');
hold on
plot(xdatP1,ff1,'.b');
plot(xdatP2,ff2,'.b');
xlabel(['R ',units]);
ylabel(['Z ', units]);
grid on
hold off

0

matlab curve-fitting polynomial-math linear-equation line-intersection

Источник

user427886 20 окт '16 в 16:56

1 ответ

Решение

Другие вопросы по тегам matlab curve-fitting polynomial-math linear-equation line-intersection

user3372061 20 окт '16 в 19:03 2016-10-20 19:03 · Accepted Answer · 2016-10-20 19:03

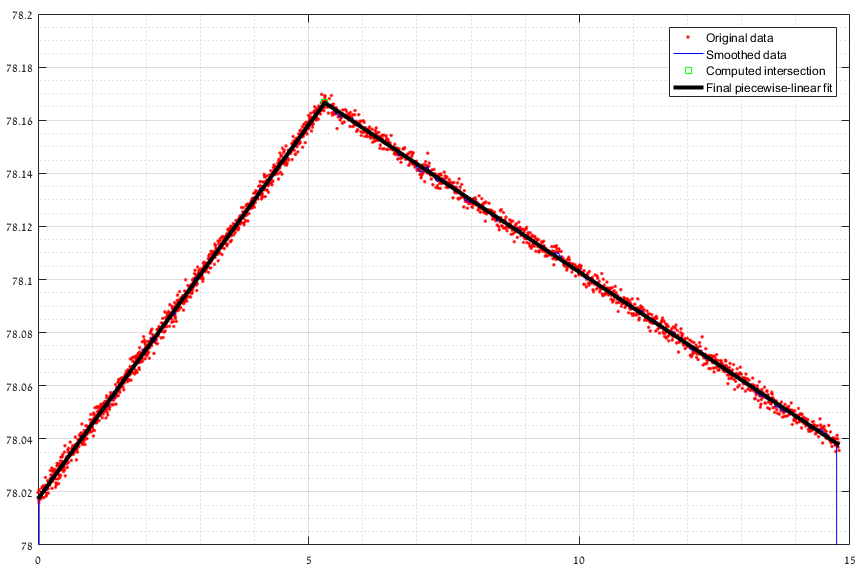
Ниже приведена грубая реализация без инструментов подгонки кривой. Хотя код должен быть понятен, вот схема алгоритма:

Мы генерируем некоторые данные.
Мы оцениваем точку пересечения, сглаживая данные и находя местоположение максимального значения.
Мы подгоняем линию к каждой стороне предполагаемой точки пересечения.
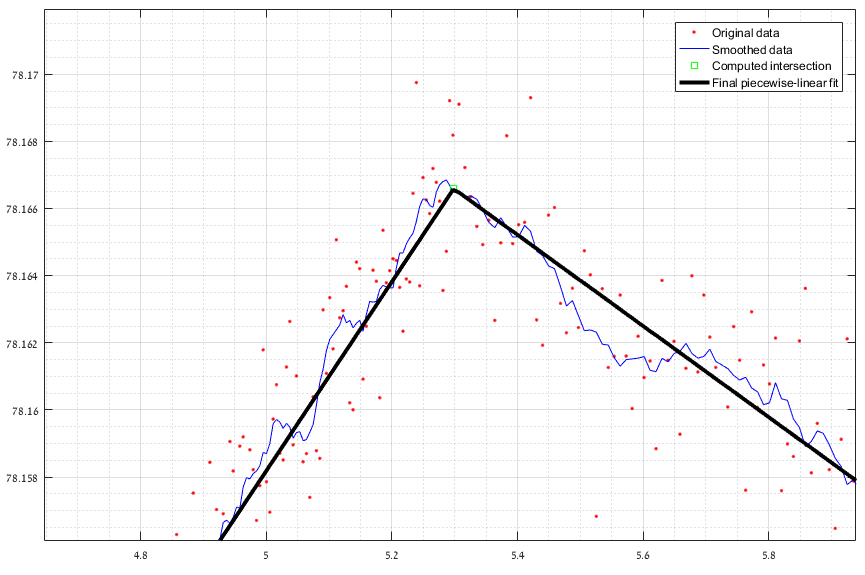
Мы вычисляем пересечение подогнанных линий, используя подогнанные уравнения.
Мы используем mkppпостроить дескриптор функции к "вычислимому" кусочному полиному.
Выход, ppfunc, это дескриптор функции 1 переменной, которую вы можете использовать, как и любую обычную функцию.

Теперь это решение не является оптимальным в каком-либо смысле (например, MMSE, LSQ и т. Д.), Но, как вы увидите в сравнении с результатом из набора инструментов MATLAB, это не так уж плохо!

function ppfunc = q40160257
%% Define the ground truth:
center_x = 6 + randn(1);
center_y = 78.15 + 0.01 * randn(1);
% Define a couple of points for the left section
leftmost_x = 0;
leftmost_y = 78.015 + 0.01 * randn(1);
% Define a couple of points for the right section
rightmost_x = 14.8;
rightmost_y = 78.02 + 0.01 * randn(1);
% Find the line equations:
m1 = (center_y-leftmost_y)/(center_x-leftmost_x);
n1 = getN(leftmost_x,leftmost_y,m1);
m2 = (rightmost_y-center_y)/(rightmost_x-center_x);
n2 = getN(rightmost_x,rightmost_y,m2);
% Print the ground truth:
fprintf(1,'The line equations are: {y1=%f*x+%f} , {y2=%f*x+%f}\n',m1,n1,m2,n2)
%% Generate some data:
NOISE_MAGNITUDE = 0.002;
N_POINTS_PER_SIDE = 1000;
x1 = linspace(leftmost_x,center_x,N_POINTS_PER_SIDE);
y1 = m1*x1+n1+NOISE_MAGNITUDE*randn(1,numel(x1));
x2 = linspace(center_x,rightmost_x,N_POINTS_PER_SIDE);
y2 = m2*x2+n2+NOISE_MAGNITUDE*randn(1,numel(x2));
X = [x1 x2(2:end)]; Y = [y1 y2(2:end)];
%% See what we have:
figure(); plot(X,Y,'.r'); hold on;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Estimating the intersection point:
MOVING_AVERAGE_PERIOD = 10; % Play around with this value.
smoothed_data = conv(Y, ones(1,MOVING_AVERAGE_PERIOD)/MOVING_AVERAGE_PERIOD, 'same');
plot(X, smoothed_data, '-b'); ylim([floor(leftmost_y*10) ceil(center_y*10)]/10);
[~,centerInd] = max(smoothed_data);
fprintf(1,'The real intersection is at index %d, the estimated is at %d.\n',...
           N_POINTS_PER_SIDE, centerInd);
%% Fitting a polynomial to each side:
p1 = polyfit(X(1:centerInd),Y(1:centerInd),1);
p2 = polyfit(X(centerInd+1:end),Y(centerInd+1:end),1);
[x_int,y_int] = getLineIntersection(p1,p2);
plot(x_int,y_int,'sg');

pp = mkpp([X(1) x_int X(end)],[p1; (p2 + [0 x_int*p2(1)])]);
ppfunc = @(x)ppval(pp,x);
plot(X, ppfunc(X),'-k','LineWidth',3)
legend('Original data', 'Smoothed data', 'Computed intersection',...
       'Final piecewise-linear fit');
grid on; grid minor;     

%% Comparison with the curve-fitting toolbox:
if license('test','Curve_Fitting_Toolbox')
  ft = fittype( '(x<=-(n2-n1)/(m2-m1))*(m1*x+n1)+(x>-(n2-n1)/(m2-m1))*(m2*x+n2)',...
                'independent', 'x', 'dependent', 'y' );
  opts = fitoptions( 'Method', 'NonlinearLeastSquares' );
  % Parameter order: m1, m2, n1, n2:
  opts.StartPoint = [0.02 -0.02 78 78];
  fitresult = fit( X(:), Y(:), ft, opts);
  % Comparison with what we did above:
  fprintf(1,[...
    'Our solution:\n'...
    '\tm1 = %-12f\n\tm2 = %-12f\n\tn1 = %-12f\n\tn2 = %-12f\n'...
    'Curve Fitting Toolbox'' solution:\n'...
    '\tm1 = %-12f\n\tm2 = %-12f\n\tn1 = %-12f\n\tn2 = %-12f\n'],...
    m1,m2,n1,n2,fitresult.m1,fitresult.m2,fitresult.n1,fitresult.n2);    
end

%% Helper functions:
function n = getN(x0,y0,m)
% y = m*x+n => n = y0-m*x0;
n = y0-m*x0;

function [x_int,y_int] = getLineIntersection(p1,p2)
% m1*x+n1 = m2*x+n2 => x = -(n2-n1)/(m2-m1)
x_int = -(p2(2)-p1(2))/(p2(1)-p1(1));
y_int = p1(1)*x_int+p1(2);

Результат (пробный прогон):

Our solution:
    m1 = 0.022982    
    m2 = -0.011863   
    n1 = 78.012992   
    n2 = 78.208973   
Curve Fitting Toolbox' solution:
    m1 = 0.022974    
    m2 = -0.011882   
    n1 = 78.013022   
    n2 = 78.209127

Увеличено вокруг пересечения: