Пролог Программирование

Question

Я сделал две программы на Прологе для головоломки nqueens, используя алгоритмы восхождения на гору и поиска луча.

К сожалению, у меня нет опыта, чтобы проверить, правильны ли программы, и я в тупике.

Я был бы признателен, если бы кто-то мог помочь мне в этом. К сожалению, программа по восхождению на холм неверна. :(Программа в поиске луча:

queens(N, Qs) :-  
  range(1, N, Ns), 
  queens(Ns, [], Qs).

range(N, N, [N]) :- !.
range(M, N, [M|Ns]) :- 
  M < N, 
  M1 is M+1, 
  range(M1, N, Ns).

queens([], Qs, Qs).
queens(UnplacedQs, SafeQs, Qs) :- 
  select(UnplacedQs, UnplacedQs1,Q),
  not_attack(SafeQs, Q),  
  queens(UnplacedQs1, [Q|SafeQs], Qs).  

not_attack(Xs, X) :- 
  not_attack(Xs, X, 1).
not_attack([], _, _) :- !.
not_attack([Y|Ys], X, N) :-
  X =\= Y+N,  
  X =\= Y-N, 
  N1 is N+1, 
  not_attack(Ys, X, N1).

select([X|Xs], Xs, X).
select([Y|Ys], [Y|Zs], X) :- select(Ys, Zs, X).

Answer 1

Я хотел бы отметить, что эта проблема является типичной проблемой удовлетворения ограничений и может быть эффективно решена с помощью модуля CSP SWI-Prolog. Вот полный алгоритм:

:- use_module(library(clpfd)).

queens(N, L) :-
    N #> 0,
    length(L, N),
    L ins 1..N,
    all_different(L),
    applyConstraintOnDescDiag(L),
    applyConstraintOnAscDiag(L),
    label(L).

applyConstraintOnDescDiag([]) :- !.
applyConstraintOnDescDiag([H|T]) :-
    insertConstraintOnDescDiag(H, T, 1),
    applyConstraintOnDescDiag(T).

insertConstraintOnDescDiag(_, [], _) :- !.
insertConstraintOnDescDiag(X, [H|T], N) :-
    H #\= X + N,
    M is N + 1,
    insertConstraintOnDescDiag(X, T, M).

applyConstraintOnAscDiag([]) :- !.
applyConstraintOnAscDiag([H|T]) :-
    insertConstraintOnAscDiag(H, T, 1),
    applyConstraintOnAscDiag(T).

insertConstraintOnAscDiag(_, [], _) :- !.
insertConstraintOnAscDiag(X, [H|T], N) :-
    H #\= X - N,
    M is N + 1,
    insertConstraintOnAscDiag(X, T, M).

N это число ферзей или размер доски ( 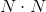), а такж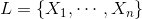е , где 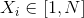, будучи положением королевы на линии ,

Давайте рассмотрим каждую часть алгоритма выше, чтобы понять, что происходит.

:- use_module(library(clpfd)).

Это указывает SWI-Prolog на загрузку модуля, содержащего предикаты для проблем удовлетворения ограничений.

queens(N, L) :-
        N #> 0,
        length(L, N),
        L ins 1..N,
        all_different(L),
        applyConstraintOnDescDiag(L),
        applyConstraintOnAscDiag(L),
        label(L).

queens Предикат является точкой входа в алгоритм и проверяет, правильно ли отформатированы термины (диапазон номеров, длина списка). Он проверяет, находятся ли королевы на разных линиях.

applyConstraintOnDescDiag([]) :- !.
applyConstraintOnDescDiag([H|T]) :-
    insertConstraintOnDescDiag(H, T, 1),
    applyConstraintOnDescDiag(T).

insertConstraintOnDescDiag(_, [], _) :- !.
insertConstraintOnDescDiag(X, [H|T], N) :-
    H #\= X + N,
    M is N + 1,
    insertConstraintOnDescDiag(X, T, M).

Он проверяет, есть ли ферзь на диагонали-потомке текущей ферзи, которая повторяется.

applyConstraintOnAscDiag([]) :- !.
applyConstraintOnAscDiag([H|T]) :-
    insertConstraintOnAscDiag(H, T, 1),
    applyConstraintOnAscDiag(T).

insertConstraintOnAscDiag(_, [], _) :- !.
insertConstraintOnAscDiag(X, [H|T], N) :-
    H #\= X - N,
    M is N + 1,
    insertConstraintOnAscDiag(X, T, M).

То же, что и предыдущий, но он проверяет, есть ли королева на восходящей диагонали.

Наконец, результаты можно узнать, вызвав предикат queens/2, такие как:

?- findall(X, queens(4, X), L).
L = [[2, 4, 1, 3], [3, 1, 4, 2]]

Answer 2

Если я правильно прочитал ваш код, алгоритм, который вы пытаетесь реализовать, - это простой поиск в глубину, а не поиск по лучу. Это нормально, потому что так и должно быть (я не вижу, насколько эффективен поиск луча для этой проблемы, и это может быть сложно для программирования).

Я не собираюсь отлаживать этот код для вас, но я дам вам совет: постройте шахматную доску снизу вверх

queens(0, []).
queens(N, [Q|Qs]) :-
    M is N-1,
    queens(M, Qs),
    between(1, N, Q),
    safe(Q, Qs).

где safe(Q,Qs) верно, если ни один из Qs атака Q, safe/2 тогда соединение простого memberchk/2 проверьте (см. руководство SWI-Prolog) и ваш not_attack/2 предикат, который на первый взгляд кажется верным.

Answer 3

Быстрая проверка в Google нашла несколько кандидатов для вас, чтобы сравнить с вашим кодом и найти, что изменить.

Моим излюбленным решением для полной ясности будет второе из тех, что связаны с выше:

% This program finds a solution to the 8 queens problem.  That is, the problem of placing 8
% queens on an 8x8 chessboard so that no two queens attack each other.  The prototype
% board is passed in as a list with the rows instantiated from 1 to 8, and a corresponding
% variable for each column.  The Prolog program instantiates those column variables as it
%  finds the solution.

% Programmed by Ron Danielson, from an idea by Ivan Bratko.

% 2/17/00


queens([]).                                 % when place queen in empty list, solution found

queens([ Row/Col | Rest]) :-                % otherwise, for each row
            queens(Rest),                   % place a queen in each higher numbered row
            member(Col, [1,2,3,4,5,6,7,8]), % pick one of the possible column positions
            safe( Row/Col, Rest).           % and see if that is a safe position
                                            % if not, fail back and try another column, until
                                            % the columns are all tried, when fail back to
                                            % previous row

safe(Anything, []).                         % the empty board is always safe

safe(Row/Col, [Row1/Col1 | Rest]) :-        % see if attack the queen in next row down
            Col =\= Col1,                   % same column?
            Col1 - Col =\= Row1 - Row,      % check diagonal
            Col1 - Col =\= Row - Row1,
            safe(Row/Col, Rest).            % no attack on next row, try the rest of board

member(X, [X | Tail]).                      % member will pick successive column values

member(X, [Head | Tail]) :-
            member(X, Tail).

board([1/C1, 2/C2, 3/C3, 4/C4, 5/C5, 6/C6, 7/C7, 8/C8]). % prototype board

Последняя ссылка, однако, решает ее тремя различными способами, чтобы вы могли сравнить ее с тремя известными решениями.