Как точно подогнать повернутую гиперболу?
Мои экспериментальные данные выглядят как кусочки гиперболы. Ниже я приведу код (Matlab), который генерирует "фиктивные" данные, которые очень похожи на исходные:
function [x_out,y_out,alpha1,alpha2,ecK,offsetX,offsetY,branchDirection] = dummyGenerator(mu_alpha)
alpha_range=0.1;
numberPoint2Return=100; % number of points to return
ecK=10.^((rand(1)-0.5)*2*2); % eccentricity-related parameter
% slope of the first asimptote (radians)
alpha1 = ((rand(1)-0.5)*alpha_range+mu_alpha);
% slope of the first asimptote (radians)
alpha2 = -((rand(1)-0.5)*alpha_range+mu_alpha);
beta = pi-abs(alpha1-alpha2); % angle between asimptotes (radians)
branchDirection = datasample([0,1],1); % where branch directed
% up: branchDirection==0;
% down: branchDirection==1;
% generate branch
x = logspace(-3,2,numberPoint2Return*100)'; %over sampling
y = (tan(pi/2-beta)*x+ecK./x);
% rotate branch using branchDirection
theta = -(pi/2-alpha1)-pi*branchDirection;
% get rotation matrix
rotM = [ cos(theta), -sin(theta);
sin(theta), cos(theta) ];
% get rotated coordinates
XY1=[x,y]*rotM;
x1=XY1(:,1); y1=XY1(:,2);
% remove possible Inf
x1(~isfinite(y1))=[];
y1(~isfinite(y1))=[];
% add noise
y1=((rand(numel(y1),1)-0.5)+y1);
% downsampling
%x_out=linspace(min(x1),max(x1),numberPoint2Return)';
x_out=linspace(-10,10,numberPoint2Return)';
y_out=interp1(x1,y1,x_out,'nearest');
% randomize offset
offsetX=(rand(1)-0.5)*50;
offsetY=(rand(1)-0.5)*50;
x_out=x_out+offsetX;
y_out=y_out+offsetY;
end
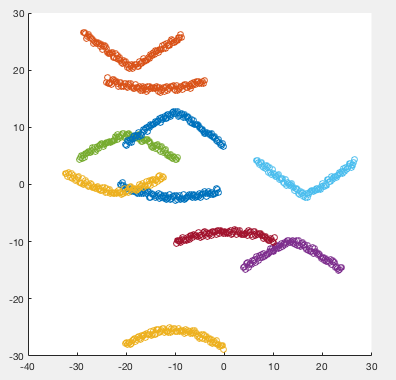
Типичные результаты представлены на рисунке:
Данные обладают следующим важным свойством: уклоны обеих асимптот происходят из одного и того же распределения (только разные знаки), поэтому для моей подгонки у меня довольно точная оценка для mu_alpha,
Теперь начинается проблемная часть. Я пытаюсь соответствовать этим точкам данных. Основная идея моего подхода состоит в том, чтобы найти вращение, чтобы получить y=k*x+b/x форма, а затем просто соответствовать ему.
Я использую следующий код:
function Rsquare = fitFunction(x,y,alpha1,alpha2,ecK,offsetX,offsetY)
R=[];
for branchDirection=[0 1]
% translate back
xt=x-offsetX;
yt=y-offsetY;
% rotate back
theta = (pi/2-alpha1)+pi*branchDirection;
rotM = [ cos(theta), -sin(theta);
sin(theta), cos(theta) ];
XY1=[xt,yt]*rotM;
x1=XY1(:,1); y1=XY1(:,2);
% get fitted values
beta = pi-abs(alpha1-alpha2);
%xf = logspace(-3,2,10^3)';
y1=y1(x1>0);
x1=x1(x1>0);
%x1=x1-min(x1);
xf=sort(x1);
yf=(tan(pi/2-beta)*xf+ecK./xf);
R(end+1)=sum((xf-x1).^2+(yf-y1).^2);
end
Rsquare=min(R);
end
К сожалению, этот код работает не очень хорошо, очень часто у меня плохие результаты, даже когда я использую известные (из моделирования) исходные параметры.
Не могли бы вы помочь мне найти хорошее решение для такой подходящей проблемы?
ОБНОВИТЬ:
Я нахожу решение (см. Ответ), но у меня все еще есть небольшая проблема - моя оценка a параметр плохой, иногда у меня не было хороших припадков по этой причине.
Не могли бы вы предложить некоторые идеи, как оценить с экспериментальной точки?
1 ответ
Я нашел основную проблему (это был мой мозг, как обычно)! Я не знал об общем уравнении гиперболы. Итак, уравнение для моих гипербол:
((Х-х0)/ а) ^2-. ((У-у0)/ б) ^2=-1.
Таким образом, мы можем не заботиться о знаке, тогда я могу использовать следующий код:
mu_alpha=pi/6;
[x,y,alpha1,alpha2,ecK,offsetX,offsetY,branchDirection] = dummyGenerator(mu_alpha);
% hyperb=@(alpha,a,x0,y0) tan(alpha)*a*sqrt(((x-x0)/a).^2+1)+y0;
hyperb=@(x,P) tan(P(1))*P(2)*sqrt(((x-P(3))./P(2)).^2+1)+P(4);
cost =@(P) fitFunction(x,y,P);
x0=mean(x);
y0=mean(y);
a=(max(x)-min(x))./20;
P0=[mu_alpha,a,x0,y0];
[P,fval] = fminsearch(cost,P0);
hold all
plot(x,y,'-o')
plot(x,hyperb(x,P))
function Rsquare = fitFunction(x,y,P)
%x=sort(x);
yf=tan(P(1))*P(2)*sqrt(((x-P(3))./P(2)).^2+1)+P(4);
Rsquare=sum((yf-y).^2);
end
PS Теги LaTex у меня не сработали