3 случайных числа из 2 случайных чисел

Question

Предположим, у вас есть некоторая функция rnd(x) с равномерным распределением, которая будет возвращать 0 или 1. Как вы можете использовать эту функцию для создания любой функции rnd(x,n), которая будет возвращать равномерно распределенные числа от 0 до n?

Я имею в виду, что все используют это, но для меня это не так умно. Например, я могу создать распределения с правой границей 2^n-1 ([0-1],[0-3],[0-7] и т. Д.), Но не могу найти способ сделать это для диапазонов как [0-2] или [0-5] без использования очень больших чисел для разумной точности.

Answer 1

Предположим, что вам нужно создать функцию rnd(n) который возвращает равномерно распределенное случайное число в диапазоне [0, n], используя другую функцию rnd1() который возвращает 0 или 1.

1. Найти такой маленький k тот 2^k >= n+1
2. Создать номер, состоящий из k биты и заполнить все его биты с помощью rnd1(), Результатом является равномерно распределенное число в диапазоне [0, 2^k-1]
3. Сравнить сгенерированное число с n, Если оно меньше или равно n, верните его. В противном случае перейдите к шагу 2.

В общем, это вариант того, как генерировать одинаковые числа в небольшом диапазоне, используя библиотечную функцию, которая генерирует числа в большом диапазоне:

unsigned int rnd(n) {
  while (true) {
    unsigned int x = rnd_full_unsigned_int();
    if (x < MAX_UNSIGNED_INT / (n+1) * (n+1)) {
      return x % (n+1);
    }
  }
}

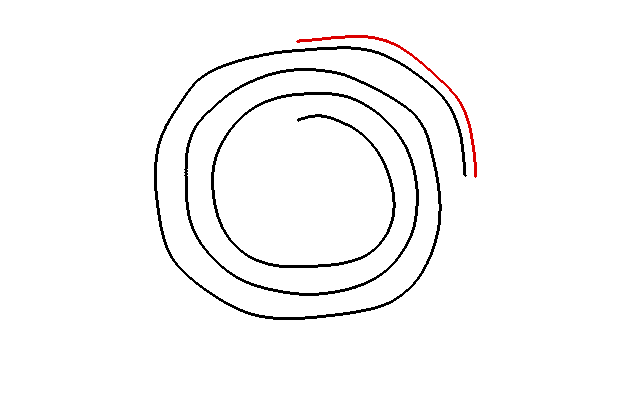
Пояснение к приведенному выше коду. Если вы просто вернетесь rnd_full_unsigned_int() % (n+1) тогда это приведет к смещению в сторону небольших чисел. Черная спираль представляет все возможные значения от 0 до MAX_UNSIGNED_INT, отсчитанные изнутри. Длина пути одного оборота равна (n+1). Красная линия показывает, почему происходит смещение. Итак, чтобы удалить это смещение, мы сначала создаем случайное число x в диапазоне [0, MAX_UNSIGNED_INT] (это легко с битовой заливкой). Затем, если x попадает в область смещения, мы воссоздаем его. Мы продолжаем его воссоздавать до тех пор, пока он не попадет в смещающий регион. х в данный момент находится в форме a*(n+1)-1, так x % (n+1) является равномерно распределенным числом [0, n].