Сравнение данных частоты и данных zipf / rank

Question

Несколько раз за эти годы я хотел работать с частотными списками (символ, слово, n-грамм и т. Д.) Различного качества, но никогда не думал, как использовать их вместе.

В то время, когда я интуитивно понимал, что списки имеют только ранг и никакие другие данные не должны быть полезными. С тех пор я узнал о законах и законах власти Ципфа. Хотя я не очень разбираюсь в математике, поэтому я не до конца понимаю все.

Я нашел несколько вопросов в Stackru и CrossValidated, которые, похоже, могут быть связаны. Но я либо не понимаю их на должном уровне, либо им не хватает полезных ответов.

То, что я хочу, - это способ нормализовать список с полными частотными данными и список только с данными ранга, чтобы я мог использовать два списка вместе.

Например, список слов с частотой данных:

word  per /million
的    50155.13
我    50147.83
你    39629.27
是    28253.52
了    28210.53
不    20543.44
在    12811.05
他    11853.78
我们  11080.02
...
...
...   00000.01

И список слов только с данными ранга:

word  rank
的    1
一    2
是    3
有    4
在    5
人    6
不    7
大    8
中    9
...
...
...   100,000

Как я могу нормализовать как данные частоты, так и данные ранга в одно и то же значение, которое затем можно использовать в сравнениях и т. Д.?

(Примеры списков в этом вопросе являются лишь примерами. Предположим, что гораздо более длинные списки получены из внешних источников, над которыми программист не имеет никакого контроля.)

Answer 1

Должно быть очевидно, что вы можете определить ранг, когда у вас есть полный список с частотами (упорядочить список по частоте в порядке убывания и назначить приращение ранга), но не наоборот (как бы вы узнали, как часто Слово встречается, учитывая информацию о том, что оно ранжируется на 3-й позиции? Вы можете только сделать вывод, что оно встречается с равной / более низкой частотой по сравнению со словом на 2-й позиции ранга и равной / более высокой частотой по сравнению со словом на 4-й позиции).

Применяя закон Ципфа, вы можете сопоставить ранжирование с некоторой оценкой частоты и попытаться приблизительно оценить частоту. Но я не уверен, насколько хорошо это обобщает для разных языков.

[править] Вы действительно привлекли мое внимание сейчас:) Я столкнулся с этим приложением Закона Ципфа о Wolfram MathWorld. Я проведу несколько небольших экспериментов с английским термином corpus, который я создал некоторое время назад. Я вернусь с результатами, просто немного терпения.

[edit2] Теперь я взял список частот из слов Частоты в письменном и устном английском: на основе Британского национального корпуса. ( это, если быть точным; который содержит только первые 5000 слов или около того, но должно быть достаточно для этого быстрого рассмотрения) и применил простую 1/rank оценить частоты. Я выполнил эксперимент в виде рабочего процесса KNIME (используя узлы JFreeChart для диаграммы и узлы Палладиана [примечание: я являюсь автором узлов Палладиана] для вычисления RMSE), который выглядит следующим образом:

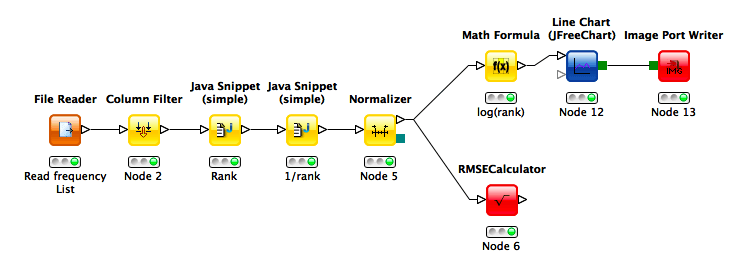
График с фактическими частотами и оценками по рангу выглядит следующим образом (ранг является логарифмическим, извините за отсутствие адекватного заголовка на оси; синяя линия - это оценка; красная линия - это фактическое значение из набора данных):

Таким образом, хотя есть некоторые выбросы на более высоких рангах (например, 2,3,4), оценка частоты все равно должна быть совершенно приличной при использовании ее в сочетании с TF-IDF или чем-то в этом роде. ( RMSE составляет ~ 0,004 в этом случае, что, конечно, связано с минимальным отклонением в длинном хвосте)

Вот фрагмент с некоторыми фактическими значениями:

Btw.; также взгляните на этот раздел статьи в Википедии о законе Ципфа, в котором приведены аналогичные результаты.