Как рассчитать позиции по оси Z
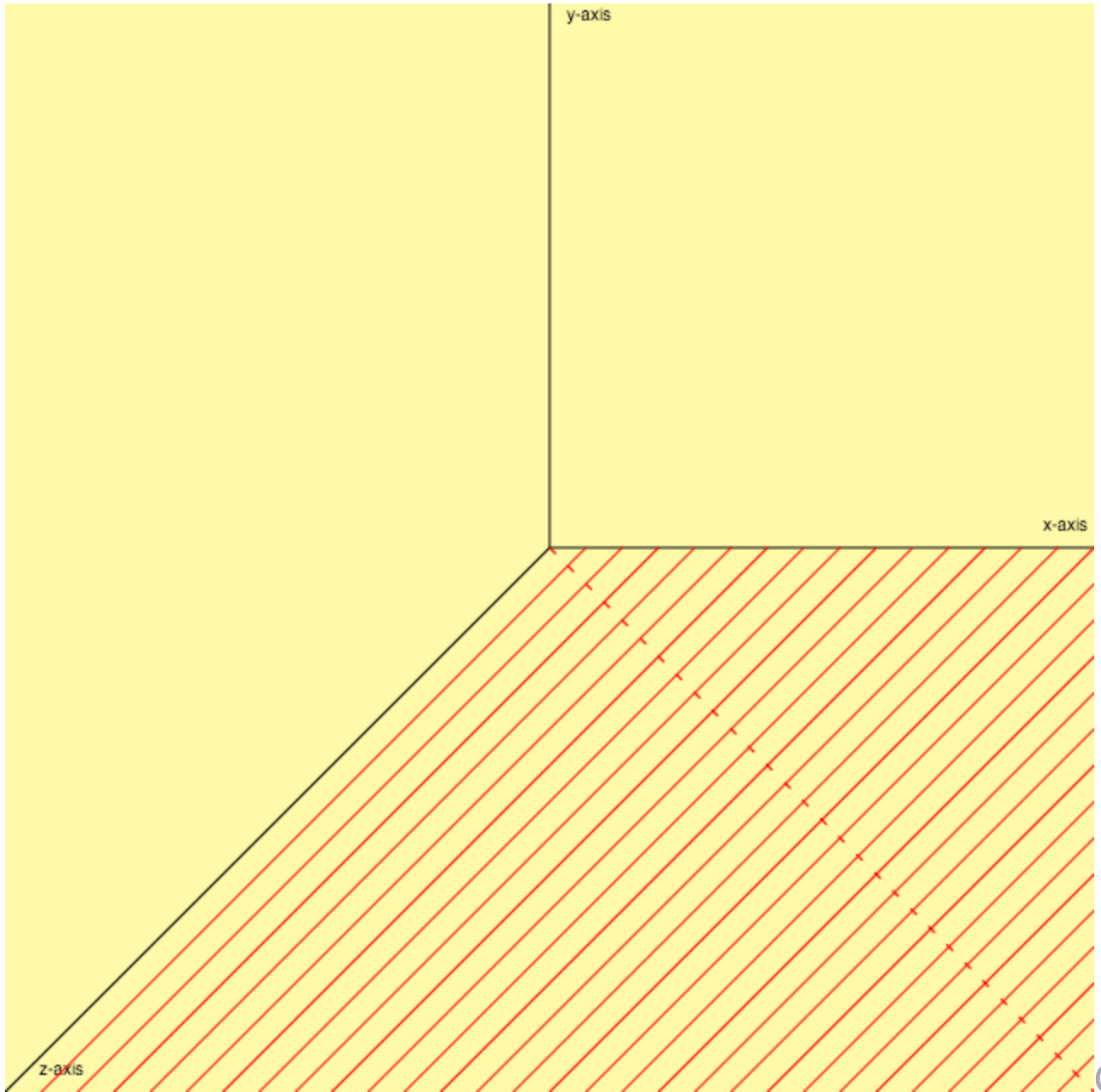
Я нарисовал простой 3-координатный граф на холсте выше;
Я определил несколько констант для работы с
var width = window.innerWidth * 0.5 , height = window.innerWidth * 0.5;
var cx = width / 2, cy = height / 2, cz = height / 2, blcx = 0, blcy = height, brcz = height, brcx = width, brcy = height;
var ySegment = height / 30;
var xSegment = width / 30;
var xSegmentRatio = xSegment / width;
var ySegmentRatio = ySegment / height;
cx и cy и cz все относятся к центру холста. blcx означает нижний левый угол-х, brcy нижний правый угол-у и т. д. Я понимаю, что это немного хакерство, так как это первая попытка сделать это, но если вы терпите меня, есть реальная концепция, которую я пытаюсь уловить здесь.
а затем нарисовал красные линии, как это:
(function() {
var gridCx = cx, gridCy = cy, gridCz = cz;
var gridBlCx = blcx, gridBlCy = brcy;
for (var i = cx; i < width; i++) {
gridCx += xSegment;
gridBlCx += ySegment;
gridCzx -= gridCzx * (xSegmentRatio / ySegmentRatio);
ctx.beginPath();
ctx.moveTo(gridCx, cy);
ctx.lineTo(gridBlCx, height);
ctx.strokeStyle="#FF0000";
ctx.stroke();
}
})();
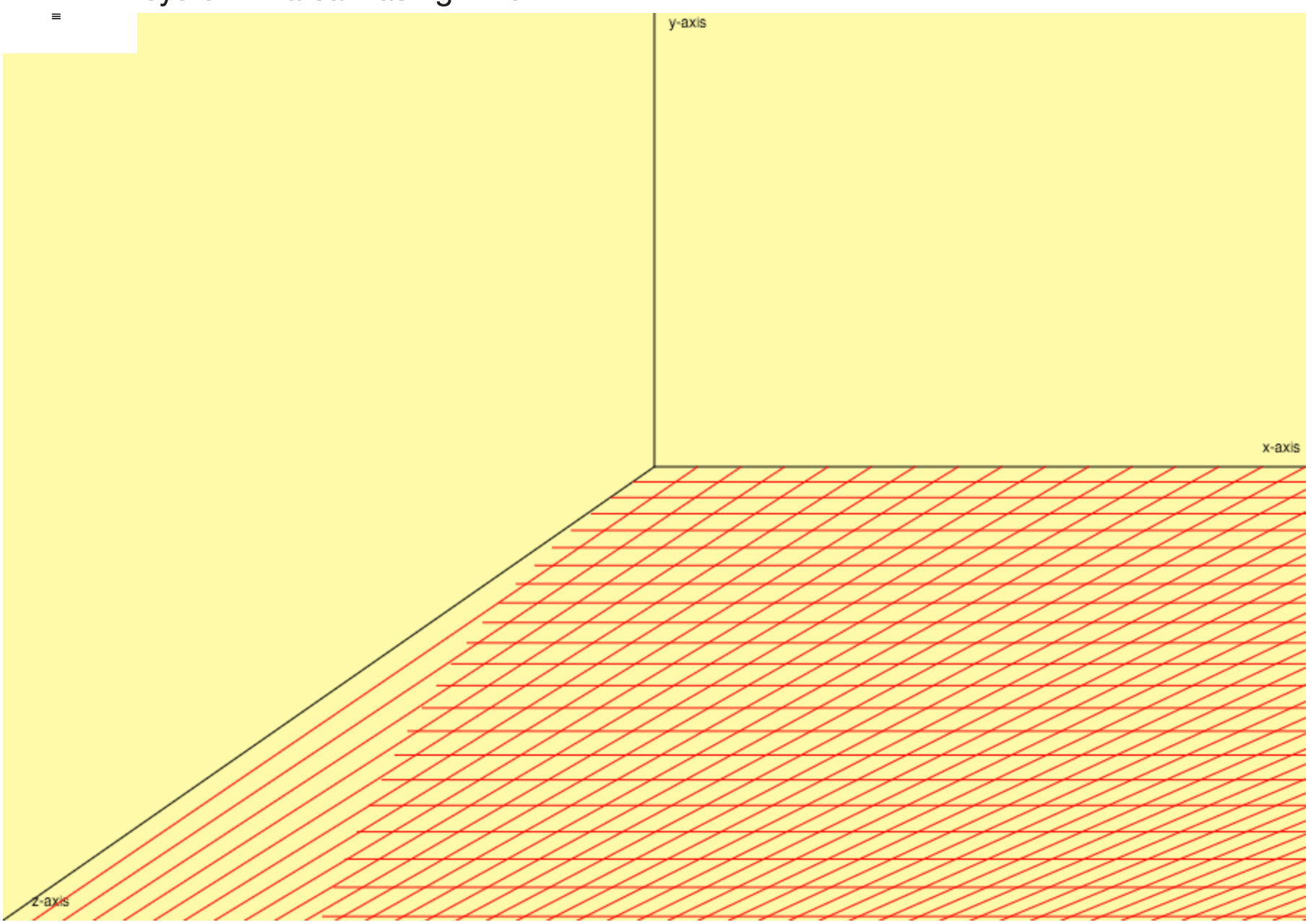
Я попробовал это:
gridCzx -= gridCzx * xSegmentRatio;
gridCzy += gridCzy * ySegmentRatio;
ctx.beginPath();
ctx.moveTo(gridCzx, gridCzy);
ctx.lineTo(width, gridCzy);
ctx.strokeStyle = "#ff0000";
ctx.stroke();
и получил это:
Но я понял, что мне не хватает фундаментальной математической концепции. Спасибо за любую информацию, которую вы можете дать! Мой основной вопрос здесь: как мне выбрать точку на оси z, учитывая расстояние от центра?
2 ответа
Преобразование 3 измерений в 2 измерения
Ось расскажет нам как двигаться
Чтобы найти точку в первом измерении x, двигайтесь вдоль оси x слева направо. Чтобы найти точку во втором измерении y, вы должны интегрировать как первое, так и второе измерения, то есть 1-й x слева направо, как только вы это получите, 2-й по оси Y вниз по экрану.
С каждым измерением вы полагаетесь на положение предыдущего измерения. Он также опирается на ось, оси x и y находятся под углом 90 градусов друг к другу, но они могут быть под углом 45 или 120 градусов, это не будет иметь никакого значения для нахождения двухмерных координат точки. Сначала вдоль оси X, затем Y вдоль оси y.
Векторные функции
Поскольку отображение только 2D, ось может быть представлена как 2D векторы. Длина вектора говорит о масштабе оси. Таким образом, для оси x, если я определяю ось как двумерный (отображать координаты) вектор (2,0), то я говорю, что он проходит 2 поперек и 0 вниз для каждой единицы в координате x. Если я хочу быть с координатой х 10, я умножаю его на ось, чтобы получить положение экрана.
Таким образом, к коду...
function screenCoord(x,y){ // creates a coordinate in screen space
// screen space is always in pixels
// screen space always has the origin (0,0) at the top left
return {
x : x,
y : y,
}
}
function screenVector(x,y){ // a vector in screen space it points in a direction
// and its is in pixels
return { // basically identical to the last function
x : x,
y : y,
}
}
Итак, давайте определим ось X, которую я имел (2,0), увеличенную на 2
var xAxis = screenVector(2,0);
Теперь положение топора скажем 10
var xPos = 10
Чтобы найти его местоположение, нам нужно получить координаты экрана вдоль оси x. Мы делаем это путем умножения xAxis на xPos. Чтобы сделать это проще, мы можем создать функцию умножения вектора
function multiply(vector, value){
var x = vector.x * value; // multiply the vector x by value
var y = vector.y * value; // multiply the vector y by value
return screenCoord(x,y)
}
Теперь, чтобы найти первый размерный pos xPos
var screenPos = multiply(xAxis, xPos); // returns the screen position of x = 10
Теперь, чтобы сделать 2-е измерение, мы добавим это к предыдущему. Давайте определим функцию для добавления вектора в другой
function add(vector1, vector2){ // adds two vectors returning a new one
var x = vector1.x + vector2.x;
var y = vector1.y + vector2.y;
return screenCoord(x,y);
}
Итак, теперь давайте создадим ось у
var yAxis = new screenVector(0,2); // y goes down the screen and has no x change
и у поз
var posY = 10;
Итак, теперь давайте сделаем это из х
var screenPosX = multiply(xAxis,posX); // get the x position on the screen
var screenPosY = multiply(yAxis,posY); // get the y position on the screen
Теперь мы добавим результаты двух координат
var screenXY = add(screenPosX,screenPosY);
И у нас есть координата на экране x = 10 и y = 10 (которая в этом случае оказывается в положении пикселя 20 через 20 вниз.
3-е измерение
Теперь не нужно много времени, чтобы угадать, что происходит для 3-го измерения z. Для x вдоль оси x, затем y вдоль оси y, а затем z вдоль оси z
Так определите ось Z
var yAxis = new screenVector(1,-1); // z axis along the diagonal from bottom left to top right
Теперь координата Z
var posZ = 10;
Таким образом, чтобы найти нашу 3 d-позицию, x вдоль ее оси, затем добавьте y вдоль ее, а затем добавьте z вдоль ее оси
var screenPosX = multiply(xAxis,posX); // get the x position on the screen
var screenPosY = multiply(yAxis,posY); // get the y position on the screen
var screenPosZ = multiply(zAxis,posZ); // get the z position on the screen
нужно сложить их вместе
var screenXY = add(screenPosX,screenPosY);
Тогда г
var screenXYZ = add(screenPosXY,screenPosZ);
и там у вас есть, как сделать преобразование из одного набора координат в другой. Это называется преобразованием
Происхождение
Мы упускаем один последний бит информации. Происхождение. Именно здесь на экране будут координаты 0,0,0 (x,y,z). Это последняя часть преобразования и в координатах экрана (x,y)
var origin = screenCoords(100,500); // set the origin at 100 pixels across 500 down
Из последнего расчета мы получили координату screenXYZ в пространстве экрана, нам нужно добавить к ней начало координат
screenXYZ = add(screenXYZ ,origin);
Теперь вы можете нарисовать пиксель с координатами (10,10,10) (x,y,z) от начала координат на 2-м экране.
Матрица
Надеюсь, это поможет, если вы поймете, что только что узнали, как использовать матрицу трехмерного преобразования. Он содержит оси x, y, z как набор из трех 2D-направлений и координаты начала координат. Матрица выполняет те же функциональные шаги, что и в простом массиве, что делает ее более эффективной, а следование некоторым правилам матрицы позволяет выполнять очень сложные преобразования. Например, если вы хотите повернуть, все, что вам нужно сделать, это изменить направление осей, и вы повернули объект. Чтобы изменить масштаб, просто измените длину оси, для перемещения объекта просто измените положение начала координат.
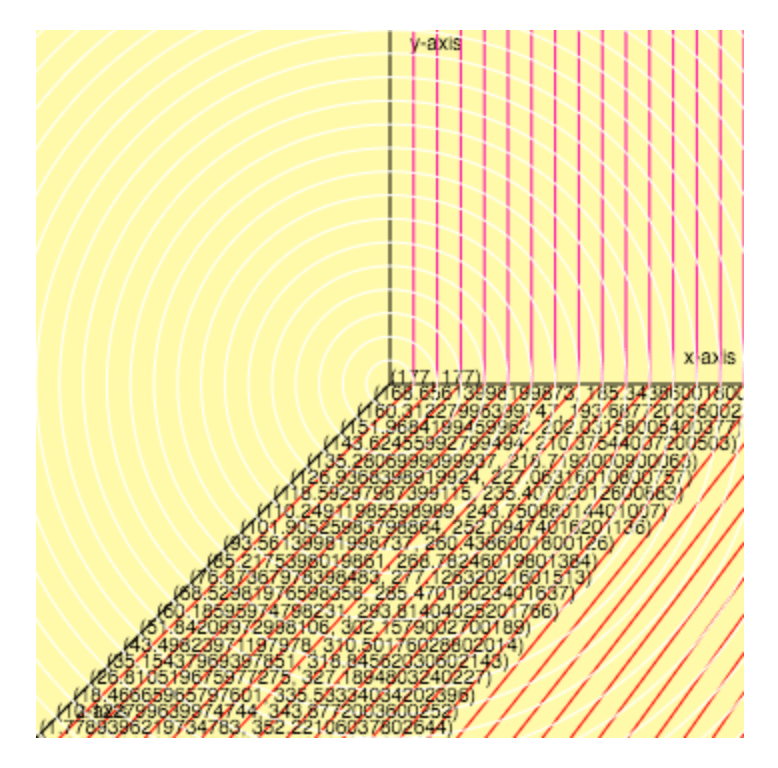
Оказывается, JavaScript Math.cos() а также Math.sin() супер полезны в этом сценарии. Я должен был думать об этом так, как если бы были последовательные концентрические круги с радиусами, начинающимися с длины моего сегмента сетки и удваивающимися для каждой последовательности. Оттуда я немного погуглил о том, как найти точку на окружности с учетом степени. Оказывается, круги, как и треугольники, имеют градусы, то есть радианы, и для направления моего z-индекса обозначено 5PI/4. Поэтому моя функция выглядит примерно так:
for (var i = 0; i < zDistance; i++) {
var r = xSegment * i;
ctx.beginPath();
ctx.arc(cx, cy, r, 0, 2 * Math.PI);
ctx.strokeStyle="white";
ctx.stroke();
var zRadian = {
divided: function() {
return 5 * Math.PI
},
divisor: function() {
return 4;
}
}
var zRadian = zRadian.divided() / zRadian.divisor();
var x = cx + r * Math.cos(zRadian);
var y = cy - r * Math.sin(zRadian);
ctx.beginPath();
ctx.fillText('(' + x + ', ' + y + ')', x, y);
ctx.stroke();
}
И вот результат: