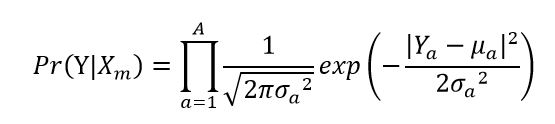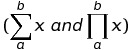Временная сложность (обозначение Big-O) вычисления апостериорной вероятности
Я получил основную идею нотации Big-O из определения нотации Big-O.
В моей задаче двумерная поверхность делится на равномерные М- сетки. Каждой сетке (m) присваивается апостериорная вероятность, основанная на признаках A.
Апостериорная вероятность m сетки рассчитывается следующим образом:
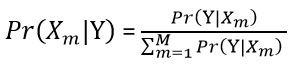
а предельная вероятность дается как:
Здесь объекты A независимы друг от друга, а сигма и средний символ представляют стандартное отклонение и среднее значение каждого объекта в каждой сетке. Мне нужно рассчитать апостериорную вероятность всех М сеток.
Какова будет временная сложность вышеупомянутой операции с точки зрения обозначения Big-O?
Я думаю, что O(M) или O(M+A). Я прав? Я ожидаю, что аутентичный ответ будет представлен на официальном форуме.
Кроме того, какова будет временная сложность, если M сеток разделить на T кластеров, где каждый кластер имеет Q сеток (Q << M) (вычисление апостериорной вероятности только для Q сеток из M сеток)?
Большое спасибо.
1 ответ
Дискретная сумма и произведение
можно понимать как петли. Если вас устраивает приближение с плавающей запятой, большинство других операторов обычно O(1), условная вероятность выглядит как вызов функции. Просто введите константы и переменные в ваше уравнение, и вы получите ожидаемый Big-O, детали формулы не имеют значения. Также имейте в виду, что эти "петли" часто можно упростить с помощью математических свойств.
Если результат неочевиден, пожалуйста, преобразуйте приведенную выше математическую формулу в реальный код программирования на языке программирования. Информатика Big-O - это никогда не формула, а фактический перевод ее на этапах программирования, в зависимости от реализации одна и та же формула может привести к очень различным сложностям выполнения. Так же, как добавление целых чисел путем фактического выполнения суммы O(n) или применения, например, формулы Гаусса O (1).
Кстати, почему вы делаете дискретную сумму на дискретном домене N? Разве это не должно быть М?