TPS - регрессия с использованием минимизации производной
Я пытаюсь найти способ сделать регрессию сплайна тонкой пластины в Python, то есть регрессии, основанной на функции стоимости следующей формы: 
который пытается минимизировать как сумму квадратов ошибок, так и вторую производную полученной функции. В идеале, я бы предпочел алгоритм, который может найти лямбду самостоятельно, используя перекрестную проверку.
Если я не ошибаюсь, R имеет две функции этого духа: сплайн stat и tps полей. Я не бегло говорю на R, поэтому я не слишком углублялся в них.
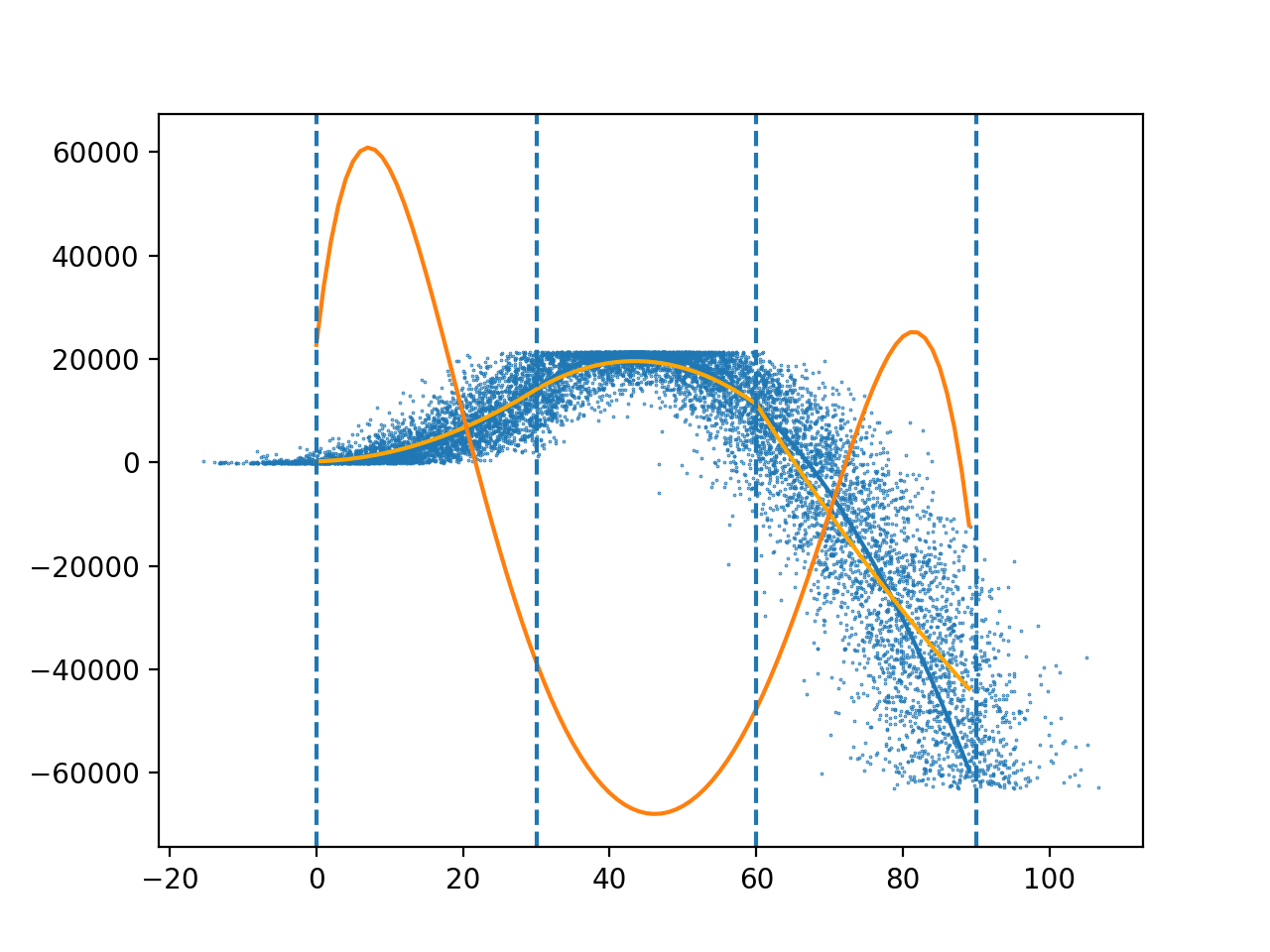
scipy.interpolate.Rbf кажется наиболее подходящим в Python, но он не ведет себя так, как я ожидаю: сглаживание = 0 не позволяет пройти через все точки данных (хотя в документации сказано, что это должно), и сглаживание ->inf превращается в линейный график (как и должно быть), но очень большие значения, кажется, просто понижают степень многочлена, даже когда это вредит как второй производной, так и ошибкам (см. оранжевый график на прилагаемом рисунке, с гладкой = 1e11).
Я неправильно использую Rbf или неправильно понимаю, что он делает? Есть ли пакет, который делает то, что я пытаюсь сделать лучше, чем Rbf?
редактировать: я нашел этот пост, который кажется очень близким к тому, что я ищу, но я надеялся, что там была нелинейная версия (которая допускает, например, f (x1, x2)), и, надеюсь, та, которая имеет API, поэтому мне не нужно менять входные данные вручную (я бы сделал это, если бы мне пришлось, но из моего опыта очень маловероятно, что нет пакета, который бы это делал)