Имитировать прыгающий мяч?

Question

Можно ли создать простую модель прыгающего мяча, используя решатели уравнения Юлии?

Я начал с этого:

using ODE

function bb(t, f)
    (y, v) = f
    dy_dt = v
    dv_dt = -9.81
    [dy_dt, dv_dt]
end

const y0 =  50.0             # height
const v0 =   0.0             # velocity
const startpos = [y0; v0]

ts = 0.0:0.25:10             # time span

t, res = ode45(bb, startpos, ts)

который производит полезные цифры:

julia> t
44-element Array{Float64,1}:
  0.0
  0.0551392
  0.25
  0.5
  0.75
  1.0
  ⋮
  8.75
  9.0
  9.25
  9.5
  9.75
 10.0

julia> res
44-element Array{Array{Float64,1},1}:
 [50.0,0.0]
 [49.9851,-0.540915]
 [49.6934,-2.4525]
 [48.7738,-4.905]
 [47.2409,-7.3575]
 ⋮
 [-392.676,-93.195]
 [-416.282,-95.6475]
 [-440.5,-98.1]

Но так или иначе это должно вмешаться, когда высота равна 0, и полностью изменить скорость. Или я не на том пути?

Answer 1

DiffrentialEquations.jl предлагает сложные обратные вызовы и обработку событий. Поскольку алгоритмы diffrentialEquations.jl работают примерно в 10 раз быстрее, предлагая интерполяцию более высокого порядка, эти алгоритмы, безусловно, лучше выбрать здесь в любом случае.

Первая ссылка - это документация, в которой показано, как выполнять обработку событий. Простой интерфейс использует макросы. Я начинаю с определения функции.

f = @ode_def BallBounce begin
  dy =  v
  dv = -g
end g=9.81

Здесь я показываю https://github.com/JuliaDiffEq/ParameterizedFunctions.jl, чтобы сделать синтаксис лучше, но вы можете определить функцию непосредственно как обновление на месте f(t,u,du) (как Sundials.jl). Затем вы определяете функцию, которая определяет, когда происходит событие. Это может быть любая функция, которая является положительной и достигает нуля во время события. Здесь мы проверяем, когда мяч падает на землю, или когда y=0, так:

function event_f(t,u) # Event when event_f(t,u,k) == 0
  u[1]
end

Далее вы говорите, что делать, когда происходит событие. Здесь мы хотим поменять знак скорости:

function apply_event!(u,cache)
  u[2] = -u[2]
end

Вы объединяете эти функции для создания обратного вызова с помощью макросов:

callback = @ode_callback begin
  @ode_event event_f apply_event!
end

Теперь вы решаете, как обычно. Вы определяете ODEProblem с помощью f и начальное условие, и вы вызываете решить на временном интервале. Единственное, что дополнительно - вы передаете обратный вызов вместе с решателем:

u0 = [50.0,0.0]
prob = ODEProblem(f,u0)
tspan = [0;15]
sol = solve(prob,tspan,callback=callback)

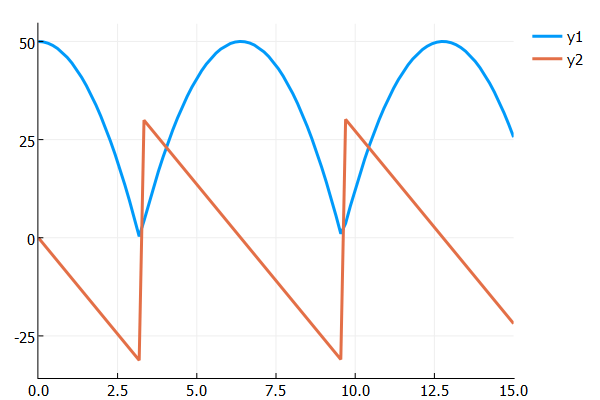
Затем мы можем использовать рецепт сюжета для автоматического построения решения:

plot(sol)

Результат таков:

Несколько вещей, чтобы заметить здесь:

1. DiffrentialEquations.jl будет автоматически использовать интерполяцию для более безопасной проверки события. Например, если событие произошло в пределах временного шага, но не в его концах, diffrentialEquations.jl все равно найдет его. В качестве опций для @ode_event макро.

2. DiffrentialEquations.jl использовал метод rootfinding, чтобы отследить момент события. Несмотря на то, что адаптивный решатель проходит мимо события, используя поиск по корню в интерполяции, он находит точное время события и, таким образом, получает правильное прерывание. Вы можете видеть это на графике, поскольку мяч никогда не становится отрицательным.

3. Это может сделать намного больше. Проверьте документы. Вы можете сделать что угодно с этим. Например, ваш ODE изменяет размер в течение прогона для моделирования популяции клеток с рождением и смертью. Это то, что другие пакеты решения не могут сделать.

4. Даже со всеми этими функциями скорость не снижается.

Дайте мне знать, если вам нужны дополнительные функциональные возможности, добавленные в макросы интерфейса "простота использования".

Answer 2

Несколько хакерский

function bb(t, f)
    (y, v) = f
    dy_dt = v
    dv_dt = -9.81*sign(y)
    [dy_dt, dv_dt]
end

где вы просто следуете соглашению, где y и -y относятся к одной и той же высоте. Затем вы можете построить траекторию прыгающего мяча, просто нарисовав abs(y).