MATLAB орбита Земли и Луны вокруг Солнца

Question

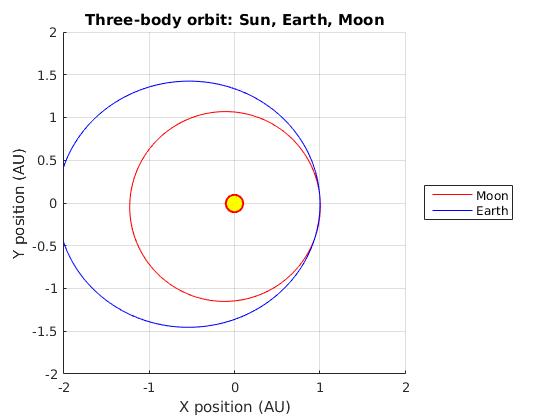Мы пытаемся построить орбиту Луны вокруг Земли, которая, в свою очередь, вращается вокруг Солнца. Мы используем метод Эйлера-Кромера. Этот код работает для симуляции планет. И это должно работать при правильных начальных условиях для более сложной установки, такой как то, что мы пытаемся сейчас с тремя телами. Наш код такой:

function [xe, ye, xm, ym] = earth_moon(me, mm)
% Constants
ms = 2e30;
ntsteps = 12;
dt = 0.001;

% Variables: Earth
xe = 1 : dt : ntsteps;
xe(1) = 1;                      % Initial x pos (AU)
ye = 1 : dt : ntsteps;
ye(1) = 0;                      % Initial y pos (AU)
vex = 0;
vey = 6.27;                     % AU/yr

% Variables: Moon
xm = 1 : dt : ntsteps;
xm(1) = 1.0027;                 % Initial x pos (AU)
ym = 1 : dt : ntsteps;
ym(1) = 0;                      % Initial y pos (AU)
vmx = 0;
vmy = 0.215 + vey;              % AU/yr

% Calculations
for i = 1 : ntsteps / dt

    rm = sqrt(xm(i)^2 + ym(i)^2);
    re = sqrt(xe(i)^2 + ye(i)^2);
    rme = sqrt((xm(i) - xe(i))^2 + (ym(i) - ye(i))^2);

    vex = vex  - 4 * pi^2 * xe(i) / re^3 * dt - 4 * pi^2 * (mm / ms) * (xe(i) - xm(i))/rme^3 * dt;
    vey = vey  - 4 * pi^2 * ye(i) / re^3 * dt - 4 * pi^2 * (mm / ms) * (ye(i) - xm(i))/rme^3 * dt;
    vmx = vmx  - 4 * pi^2 * xm(i) / rm^3 * dt - 4 * pi^2 * (me / ms) * (xm(i) - xe(i))/rme^3 * dt;
    vmy = vmy  - 4 * pi^2 * ym(i) / rm^3 * dt - 4 * pi^2 * (me / ms) * (ym(i) - ye(i))/rme^3 * dt;

    xm(i + 1) = xm(i) + vmx * dt;
    ym(i + 1) = ym(i) + vmy * dt;

    xe(i + 1) = xe(i) + vex * dt;
    ye(i + 1) = ye(i) + vey * dt;

end

end

И сценарий выглядит следующим образом:

clear 
clc

me = 5.97237e24;
mm = 7.3477e22;
[xe, ye, xm, ym] = earth_moon(me, mm);

hold on;
plot(xm, ym, 'r');
plot(xe, ye, 'b');
plot(0, 0, 'r.', 'Markersize', 50);
plot(0, 0, 'y.', 'Markersize', 40);

grid on;
axis square;
xlabel('X position (AU)');
ylabel('Y position (AU)');
ylim([-2, 2])
xlim([-2, 2])
title('Three-body orbit: Sun, Earth, Moon');
text(2, 5.5, strcat('Earth: ', num2str(me), ' kg'));
text(3.5, 4.5, strcat('Moon: ', num2str(mm), ' kg'));
legend('Moon', 'Earth', 'Location', 'eastoutside');

Но мы просто не можем заставить луну сотрудничать. Какие-либо предложения?

Спасибо!