Three.js Проектор и объекты Ray
Я пытался работать с классами Projector и Ray, чтобы сделать некоторые демонстрации обнаружения столкновений. Я начал просто пытаться использовать мышь, чтобы выбрать объекты или перетащить их. Я рассмотрел примеры, в которых используются объекты, но ни один из них, похоже, не имеет комментариев, объясняющих, что именно делают некоторые методы Projector и Ray. У меня есть пара вопросов, на которые, я надеюсь, кому-то будет легко ответить.
Что именно происходит и в чем разница между Projector.projectVector() и Projector.unprojectVector()? Я заметил, что во всех примерах, использующих как проектор, так и объекты луча, внепроектный метод вызывается до создания луча. Когда бы вы использовали projectVector?
Я использую следующий код в этой демонстрации, чтобы вращать куб при перетаскивании мышью. Может кто-нибудь объяснить простыми словами, что именно происходит, когда я снимаю проект с помощью мыши и камеры, а затем создаю Луч. Зависит ли луч от вызова unprojectVector ()
/** Event fired when the mouse button is pressed down */
function onDocumentMouseDown(event) {
event.preventDefault();
mouseDown = true;
mouse3D.x = mouse2D.x = mouseDown2D.x = (event.clientX / window.innerWidth) * 2 - 1;
mouse3D.y = mouse2D.y = mouseDown2D.y = -(event.clientY / window.innerHeight) * 2 + 1;
mouse3D.z = 0.5;
/** Project from camera through the mouse and create a ray */
projector.unprojectVector(mouse3D, camera);
var ray = new THREE.Ray(camera.position, mouse3D.subSelf(camera.position).normalize());
var intersects = ray.intersectObject(crateMesh); // store intersecting objects
if (intersects.length > 0) {
SELECTED = intersects[0].object;
var intersects = ray.intersectObject(plane);
}
}
/** This event handler is only fired after the mouse down event and
before the mouse up event and only when the mouse moves */
function onDocumentMouseMove(event) {
event.preventDefault();
mouse3D.x = mouse2D.x = (event.clientX / window.innerWidth) * 2 - 1;
mouse3D.y = mouse2D.y = -(event.clientY / window.innerHeight) * 2 + 1;
mouse3D.z = 0.5;
projector.unprojectVector(mouse3D, camera);
var ray = new THREE.Ray(camera.position, mouse3D.subSelf(camera.position).normalize());
if (SELECTED) {
var intersects = ray.intersectObject(plane);
dragVector.sub(mouse2D, mouseDown2D);
return;
}
var intersects = ray.intersectObject(crateMesh);
if (intersects.length > 0) {
if (INTERSECTED != intersects[0].object) {
INTERSECTED = intersects[0].object;
}
}
else {
INTERSECTED = null;
}
}
/** Removes event listeners when the mouse button is let go */
function onDocumentMouseUp(event) {
event.preventDefault();
/** Update mouse position */
mouse3D.x = mouse2D.x = (event.clientX / window.innerWidth) * 2 - 1;
mouse3D.y = mouse2D.y = -(event.clientY / window.innerHeight) * 2 + 1;
mouse3D.z = 0.5;
if (INTERSECTED) {
SELECTED = null;
}
mouseDown = false;
dragVector.set(0, 0);
}
/** Removes event listeners if the mouse runs off the renderer */
function onDocumentMouseOut(event) {
event.preventDefault();
if (INTERSECTED) {
plane.position.copy(INTERSECTED.position);
SELECTED = null;
}
mouseDown = false;
dragVector.set(0, 0);
}
4 ответа
По сути, вам нужно проецировать из трехмерного пространства мира и двумерного пространства экрана.
Рендереры используют projectVector для перевода 3D-точек на 2D-экран. unprojectVector в основном для того, чтобы делать обратные, не проецирующие 2D точки в трехмерный мир. Для обоих методов вы передаете камеру, через которую вы просматриваете сцену.
Итак, в этом коде вы создаете нормализованный вектор в 2D-пространстве. Честно говоря, я никогда не был слишком уверен в z = 0.5 логика.
mouse3D.x = (event.clientX / window.innerWidth) * 2 - 1;
mouse3D.y = -(event.clientY / window.innerHeight) * 2 + 1;
mouse3D.z = 0.5;
Затем этот код использует матрицу проецирования камеры, чтобы преобразовать ее в наше трехмерное мировое пространство.
projector.unprojectVector(mouse3D, camera);
Теперь, когда курсор mouse3D преобразован в трехмерное пространство, мы можем использовать его для определения направления, а затем с помощью положения камеры отбрасывать луч.
var ray = new THREE.Ray(camera.position, mouse3D.subSelf(camera.position).normalize());
var intersects = ray.intersectObject(plane);
Я обнаружил, что мне нужно пойти немного глубже под поверхность, чтобы работать за пределами области действия примера кода (например, иметь холст, который не заполняет экран, или иметь дополнительные эффекты). Я написал пост в блоге об этом здесь. Это сокращенная версия, но она должна охватывать почти все, что я нашел.
Как это сделать
Следующий код (аналогичный тому, который уже был предоставлен @mrdoob) изменит цвет куба при нажатии:
var mouse3D = new THREE.Vector3( ( event.clientX / window.innerWidth ) * 2 - 1, //x
-( event.clientY / window.innerHeight ) * 2 + 1, //y
0.5 ); //z
projector.unprojectVector( mouse3D, camera );
mouse3D.sub( camera.position );
mouse3D.normalize();
var raycaster = new THREE.Raycaster( camera.position, mouse3D );
var intersects = raycaster.intersectObjects( objects );
// Change color if hit block
if ( intersects.length > 0 ) {
intersects[ 0 ].object.material.color.setHex( Math.random() * 0xffffff );
}
В более свежих выпусках three.js (около r55 и более поздних) вы можете использовать pickingRay, который еще больше упрощает ситуацию, так что это становится:
var mouse3D = new THREE.Vector3( ( event.clientX / window.innerWidth ) * 2 - 1, //x
-( event.clientY / window.innerHeight ) * 2 + 1, //y
0.5 ); //z
var raycaster = projector.pickingRay( mouse3D.clone(), camera );
var intersects = raycaster.intersectObjects( objects );
// Change color if hit block
if ( intersects.length > 0 ) {
intersects[ 0 ].object.material.color.setHex( Math.random() * 0xffffff );
}
Давайте придерживаться старого подхода, поскольку он дает больше понимания того, что происходит под капотом. Вы можете увидеть это здесь, просто нажмите на куб, чтобы изменить его цвет.
Что происходит?
var mouse3D = new THREE.Vector3( ( event.clientX / window.innerWidth ) * 2 - 1, //x
-( event.clientY / window.innerHeight ) * 2 + 1, //y
0.5 ); //z
event.clientX это координата х позиции щелчка. Разделить на window.innerWidth дает позицию щелчка в пропорции от полной ширины окна. По сути, это перевод с экранных координат, которые начинаются с (0,0) в верхнем левом углу до (window.innerWidth, window.innerHeight) внизу справа, к декартовым координатам с центром (0,0) и в диапазоне от (-1,-1) до (1,1), как показано ниже:
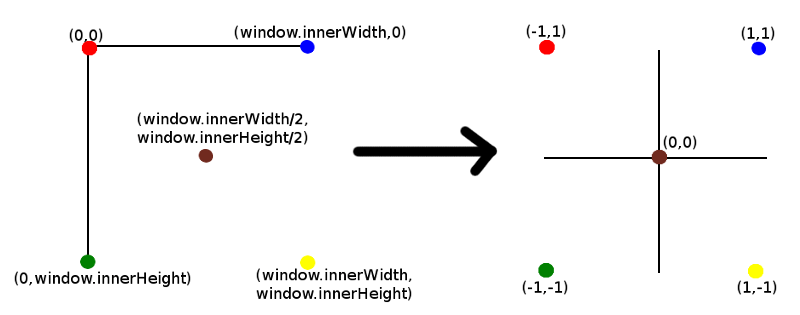
Обратите внимание, что z имеет значение 0,5. Я не буду вдаваться в подробности о значении z в этой точке, за исключением того, что скажу, что это глубина точки от камеры, которую мы проецируем в трехмерное пространство вдоль оси z. Подробнее об этом позже.
Следующий:
projector.unprojectVector( mouse3D, camera );
Если вы посмотрите на код three.js, то увидите, что это действительно инверсия матрицы проекции из трехмерного мира в камеру. Имейте в виду, что для того, чтобы перейти от координат трехмерного мира к проекции на экран, трехмерный мир необходимо проецировать на двухмерную поверхность камеры (то, что вы видите на экране). Мы в основном делаем обратное.
Обратите внимание, что mouse3D теперь будет содержать это непроецированное значение. Это положение точки в трехмерном пространстве вдоль интересующего нас луча / траектории. Точная точка зависит от значения z (мы увидим это позже).
На этом этапе может быть полезно взглянуть на следующее изображение:
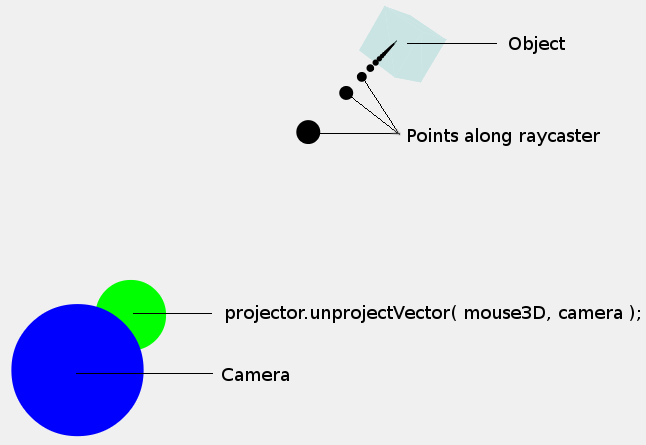
Точка, которую мы только что рассчитали (mouse3D), показана зеленой точкой. Обратите внимание, что размер точек является чисто иллюстративным, они не имеют никакого отношения к размеру точки камеры или мыши. Нас больше интересуют координаты в центре точек.
Теперь мы хотим не просто одну точку в трехмерном пространстве, а вместо этого мы хотим луч / траекторию (показанную черными точками), чтобы мы могли определить, расположен ли объект вдоль этого луча / траектории. Обратите внимание, что точки, показанные вдоль луча, являются просто произвольными точками, луч - это направление от камеры, а не набор точек.
К счастью, поскольку у нас есть точка вдоль луча, и мы знаем, что траектория должна пройти от камеры до этой точки, мы можем определить направление луча. Поэтому следующим шагом является вычитание положения камеры из положения mouse3D, что даст вектор направления, а не только одну точку:
mouse3D.sub( camera.position );
mouse3D.normalize();
Теперь у нас есть направление от камеры к этой точке в трехмерном пространстве (mouse3D теперь содержит это направление). Затем он превращается в единичный вектор путем его нормализации.
Следующим шагом является создание луча (Raycaster), начиная с положения камеры и используя направление (mouse3D) для наведения луча:
var raycaster = new THREE.Raycaster( camera.position, mouse3D );
Остальная часть кода определяет, пересекаются ли объекты в трехмерном пространстве лучом или нет. К счастью, это все о нас позаботились, используя intersectsObjects,
Демо
Итак, давайте посмотрим на демонстрацию с моего сайта, которая показывает, как эти лучи отливаются в трехмерном пространстве. Когда вы щелкаете в любом месте, камера вращается вокруг объекта, чтобы показать вам, как излучается луч. Обратите внимание, что когда камера возвращается в исходное положение, вы видите только одну точку. Это связано с тем, что все остальные точки расположены вдоль линии проекции и поэтому не видны передней точке. Это похоже на то, когда вы смотрите вниз по линии стрелки, указывающей прямо от вас - все, что вы видите, является основой. Конечно, то же самое относится и к взгляду вниз по линии стрелки, которая направляется прямо к вам (вы видите только голову), что обычно является плохой ситуацией.
Координата z
Давайте еще раз посмотрим на эту координату Z. Обратитесь к этой демонстрации, прочитав этот раздел, и поэкспериментируйте с различными значениями для z.
Хорошо, давайте еще раз посмотрим на эту функцию:
var mouse3D = new THREE.Vector3( ( event.clientX / window.innerWidth ) * 2 - 1, //x
-( event.clientY / window.innerHeight ) * 2 + 1, //y
0.5 ); //z
Мы выбрали 0,5 в качестве значения. Ранее я упоминал, что координата z определяет глубину проекции в 3D. Итак, давайте посмотрим на различные значения для z, чтобы увидеть, какой эффект это имеет. Для этого я поместил синюю точку там, где находится камера, и линию зеленых точек от камеры до непроецированного положения. Затем, после того как пересечения были рассчитаны, я перемещаю камеру назад и в сторону, чтобы показать луч. Лучше всего увидеть несколько примеров.
Во-первых, аз значение 0,5:

Обратите внимание на зеленую линию точек от камеры (синяя точка) до непроецированного значения (координата в трехмерном пространстве). Это похоже на ствол пистолета, указывающий в том направлении, в котором их луч должен быть брошен. Зеленая линия по существу представляет направление, которое вычисляется до нормализации.
Хорошо, давайте попробуем значение 0,9:
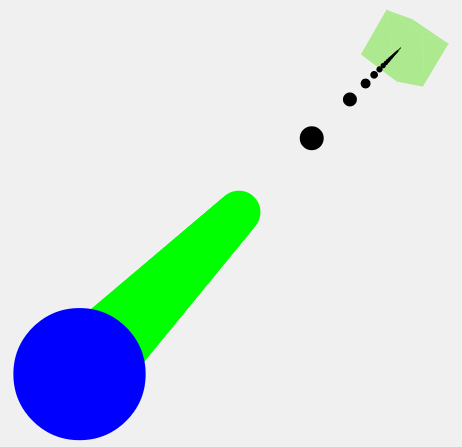
Как вы можете видеть, зеленая линия теперь расширилась в трехмерном пространстве. 0,99 распространяется еще дальше.
Я не знаю, есть ли какое-либо значение относительно того, насколько велико значение z. Кажется, что большее значение будет более точным (например, более длинный ствол орудия), но, поскольку мы рассчитываем направление, даже короткое расстояние должно быть довольно точным. Примеры, которые я видел, используют 0.5, поэтому я буду придерживаться этого, если не указано иное.
Проекция, когда холст не на весь экран
Теперь, когда мы знаем немного больше о том, что происходит, мы можем выяснить, какими должны быть значения, когда холст не заполняет окно и располагается на странице. Скажем, например, что:
- div, содержащий холст three.js, имеет offsetX слева и offsetY сверху экрана.
- холст имеет ширину, равную viewWidth, и высоту, равную viewHeight.
Код будет тогда:
var mouse3D = new THREE.Vector3( ( event.clientX - offsetX ) / viewWidth * 2 - 1,
-( event.clientY - offsetY ) / viewHeight * 2 + 1,
0.5 );
По сути, мы рассчитываем положение щелчка мыши относительно холста (для x: event.clientX - offsetX). Затем мы пропорционально определяем, где произошел щелчок (для х: /viewWidth) похоже на то, когда холст заполнял окно.
Вот и все, надеюсь, это поможет.
Начиная с выпуска r70, Projector.unprojectVector а также Projector.pickingRay устарели. Вместо этого мы имеем raycaster.setFromCamera что облегчает поиск объектов под указателем мыши.
var mouse = new THREE.Vector2();
mouse.x = (event.clientX / window.innerWidth) * 2 - 1;
mouse.y = -(event.clientY / window.innerHeight) * 2 + 1;
var raycaster = new THREE.Raycaster();
raycaster.setFromCamera(mouse, camera);
var intersects = raycaster.intersectObjects(scene.children);
intersects[0].object дает объект под указателем мыши и intersects[0].point дает точку на объекте, где был нажат указатель мыши.
Projector.unprojectVector() обрабатывает vec3 как позицию. Во время процесса вектор переводится, поэтому мы используем .sub(camera.position) на нем. Плюс нам нужно нормализовать его после этой операции.
Я добавлю немного графики в этот пост, но сейчас я могу описать геометрию операции.
Мы можем думать о камере как о пирамиде с точки зрения геометрии. Мы на самом деле определяем его с 6 панелями - слева, справа, сверху, снизу, рядом и далеко (рядом с плоскостью, ближайшей к вершине).
Если бы мы стояли в каком-то 3d и наблюдали за этими операциями, мы бы увидели эту пирамиду в произвольном положении с произвольным вращением в пространстве. Допустим, что происхождение этой пирамиды находится на ее вершине, а ее отрицательная ось Z направлена вниз.
Все, что в конечном итоге будет заключено в эти 6 плоскостей, будет отображаться на нашем экране, если мы применим правильную последовательность матричных преобразований. Который я opengl идти что-то вроде этого:
NDC_or_homogenous_coordinates = projectionMatrix * viewMatrix * modelMatrix * position.xyzw;
Это переносит нашу сетку из ее объектного пространства в мировое пространство, в пространство камеры и, наконец, проецирует матрицу перспективной проекции, которая по существу помещает все в небольшой куб (NDC с диапазонами от -1 до 1).
Пространство объекта может быть аккуратным набором координат XYZ, в котором вы генерируете что-то процедурно или, скажем, 3D-модель, которую художник моделирует с использованием симметрии и, таким образом, аккуратно сидит на одной линии с координатным пространством, в отличие от архитектурной модели, полученной из, скажем, чего-то вроде REVIT или AutoCAD.
ObjectMatrix может происходить между матрицей модели и матрицей представления, но об этом обычно заботятся заранее. Скажем, переключение y и z или приведение модели, которая находится далеко от начала координат, в границы, преобразование единиц измерения и т. Д.
Если мы думаем о нашем плоском 2-мерном экране как о глубине, его можно описать так же, как куб NDC, хотя и слегка искаженный. Вот почему мы поставляем соотношение сторон камеры. Если мы представим квадрат размером с нашу высоту экрана, то остальное это соотношение сторон, которое нам нужно, чтобы масштабировать наши координаты x.
Теперь вернемся к трехмерному пространству.
Мы стоим в трехмерной сцене и видим пирамиду. Если мы обрежем все вокруг пирамиды, а затем возьмем пирамиду вместе с частью сцены, содержащейся в ней, и поместим ее кончик в 0,0,0, и укажем основание в направлении оси -z, мы окажемся здесь:
viewMatrix * modelMatrix * position.xyzw
Умножение этого на матрицу проекции будет таким же, как если бы мы взяли наконечник и начали вытягивать его по оси X и Y, создавая квадрат из этой одной точки и превращая пирамиду в прямоугольник.
В этом процессе поле масштабируется до -1 и 1, и мы получаем нашу перспективную проекцию, и мы в конечном итоге здесь:
projectionMatrix * viewMatrix * modelMatrix * position.xyzw;
В этом пространстве у нас есть контроль над двумерным событием мыши. Поскольку он находится на нашем экране, мы знаем, что он двухмерный и что-то внутри куба NDC. Если он двумерный, мы можем сказать, что мы знаем X и Y, но не Z, следовательно, требуется литье лучей.
Поэтому, когда мы отбрасываем луч, мы в основном посылаем линию через куб, перпендикулярную одной из его сторон.
Теперь нам нужно выяснить, попадает ли этот луч в что-то на сцене, и для этого нам нужно преобразовать луч из этого куба в некоторое пространство, подходящее для вычислений. Мы хотим луч в мировом пространстве.
Луч - это бесконечная линия в пространстве. Он отличается от вектора, потому что у него есть направление, и он должен проходить через точку в пространстве. И действительно, именно так Raycaster принимает свои аргументы.
Поэтому, если мы сжимаем верхнюю часть прямоугольника вместе с линией обратно в пирамиду, линия будет исходить от вершины и будет проходить вниз и пересекать нижнюю часть пирамиды где-то между - mouse.x * farRange и -mouse.y * farRange.
(-1 и 1 сначала, но пространство просмотра в мировом масштабе, только что повернуто и перемещено)
Так как это, так сказать, местоположение камеры по умолчанию (это объектное пространство), если мы применим его собственную мировую матрицу к лучу, мы преобразуем ее вместе с камерой.
Поскольку луч проходит через 0,0,0, у нас есть только его направление, а THREE.Vector3 имеет метод для преобразования направления:
THREE.Vector3.transformDirection()
Это также нормализует вектор в процессе.
Координата Z в методе выше
По сути, это работает с любым значением и действует одинаково из-за способа работы куба NDC. Ближняя и дальняя плоскости проецируются на -1 и 1.
Поэтому, когда вы говорите, стреляйте лучом в:
[ mouse.x | mouse.y | someZpositive ]
Вы отправляете линию через точку (mouse.x, mouse.y, 1) в направлении (0,0,someZpositive)
Если вы связываете это с примером прямоугольника / пирамиды, эта точка находится внизу, и, поскольку линия исходит от камеры, она также проходит через эту точку.
НО, в пространстве НДЦ эта точка растягивается до бесконечности, и эта линия оказывается параллельной левой, верхней, правой и нижней плоскостям.
Отказ от проецирования с помощью вышеуказанного метода превращает это в положение / точку по существу. Дальняя плоскость просто отображается в мировом пространстве, поэтому наша точка находится где-то на z=-1, между аспектом -camera и + cameraAspect на X и -1 и 1 на y.
поскольку это точка, применение мировой матрицы камер не только повернет, но и переведет. Отсюда необходимость вернуть это в исходное положение путем вычитания положения камеры.