Извлечение вероятностей и наиболее вероятного разбора дерева из Cyk

Question

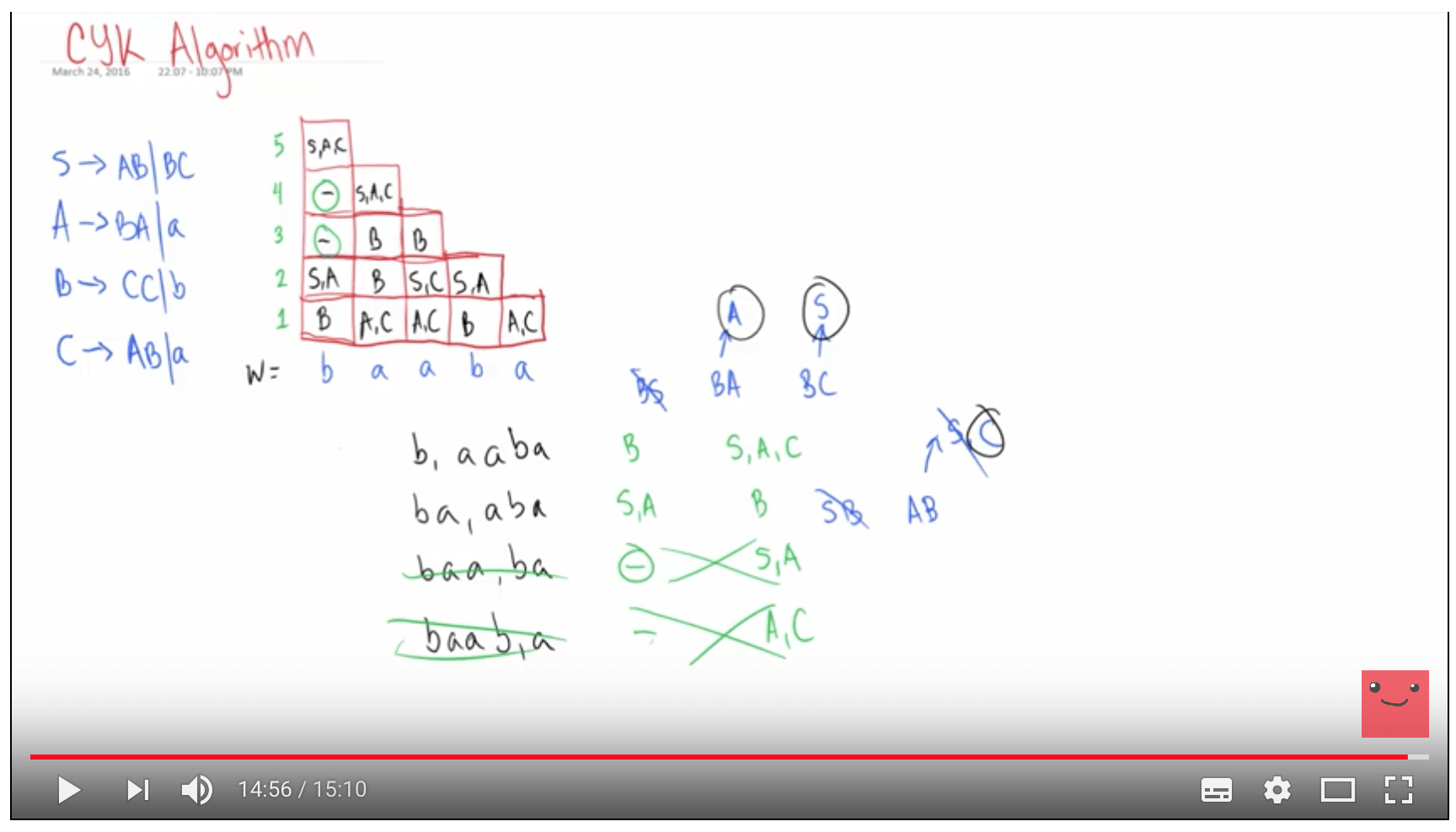
Чтобы понять алгоритм cyk, я проработал пример на: https://www.youtube.com/watch?v=VTH1k-xiswM&feature=youtu.be.

Результатом чего является:

Как извлечь вероятности, связанные с каждым разбором, и извлечь наиболее вероятное дерево разбора?

Answer 1

Это две разные проблемы для PCFG:

• признание: относится ли предложение к языку, сгенерированному CFG? (вывод: да или нет)
• парсинг: какое дерево наивысшего балла для этого предложения? (вывод: дерево разбора)

Видео с алгоритмом CKY, приведенное в этом вопросе, касается только проблемы распознавания. Чтобы выполнить задачу синтаксического анализа одновременно, нам нужно (i) поддерживать оценку каждого элемента синтаксического анализа и (ii) отслеживать иерархические отношения (например, если мы используем правило S -> NP VP: мы должны отслеживать, какой NP и какой VP используется для прогнозирования S).

Условные обозначения:

• Элемент синтаксического анализа [X, i, j]: s означает, что существует узел, помеченный X охватывающим токеном i (включенным) в j (исключенным) со счетом s. Оценка - это логарифмическая вероятность поддерева, укорененного в X,
• Предложение представляет собой последовательность слов w_1 w_2 ... w_n,

На абстрактном уровне разбор PCFG может быть сформулирован как набор правил вывода:

1. Правило сканирования (чтение токенов)

   ____________________________{precondition: X -> w_i is a grammar rule
   [X, i, i+1]: log p(X -> w_i)
   

   Блеск: если есть правило X -> w_i в грамматике, то мы можем добавить элемент [X, i, i+1] по графику.

2. Полное правило (создайте новую составляющую снизу вверх)

   [X, i, k]: s1     [Y, k, j]: s2
   _____________________________________{precondition: Z -> X Y is a grammar rule
   [Z, i, j]: s1 + s2 + log p(Z -> X, Y)
   

   Блеск: если есть 2 элемента для разбора [X, i, k] а также [Y, k, j] в графике, и правило Z -> X Y в грамматике, то мы можем добавить [Z, i, j] на график.

Цель взвешенного разбора - вывести элемент разбора [S, 0, n]:s (S: аксиома, n: длина предложения) с наибольшим количеством баллов s,

Псевдокод для всего алгоритма

# The chart stores parsing items and their scores
chart[beginning(int)][end(int)][NonTerminal][score(float)]

# the backtrack table is used to recover the parse tree at the end
backtrack[beginning][end][NonTerminal][item_left, item_right]

# insert a new item in the chart
# for a given span (i, j) and nonterminal X, we only need to
# keep the single best scoring item.
def insert(X, i, j, score, Y, Z, k):
    if X not in chart[i][j] or chart[i][j][X] < score             
        chart[i][j][X] <- score
        backtrack[i][j][X] <- (Y, i, k), (Z, k, j)

n <- length of sentence

for i in range(0, n):
    # apply scan rule
    insert(X, i, i+1, log p(X -> w_i)) for each grammar rule X -> w_i

for span_length in range(2, n):
    for beginning in range(0, n - span_length):
        end <- beginning + span_length

        for k in range(beginning+1, end -1):
            # apply completion rules
            for each grammar rule X -> Y Z such that 
                * Y is in chart[beginning][k]
                * Z is in chart[k][end]

                score_left <- chart[beginning][k][Y]
                score_right <- chart[k][end][Z]

                insert(X, beginning, end, log p(X -> Y Z) + score_left + score_right)

if there is S (axiom) in chart[0][n], then parsing is successful
    the score (log probability) of the best tree is chart[0][n][S]
    the best tree can be recovered recursively by following pointers from backtrack[0][n][S]
else:
    parsing failure, the sentence does not belong to the language
    generated by the grammar

Некоторые заметки:

• Временная сложность O(n^3 ⋅ |G|), где | G | это размер грамматики.
• Алгоритм предполагает, что грамматика имеет нормальную форму Хомского