Нахождение лучшего пути с учетом трансформации расстояния
Учитывая преобразование расстояния карты с препятствиями, как получить путь с наименьшей стоимостью от начального до целевого? Изображение с преобразованием расстояния имеет расстояние (евклидово) до ближайшего препятствия исходной карты в каждом пикселе, т.е. если в исходной карте пиксель (i,j) находится на расстоянии 3 пикселя влево и на 2 пикселя вниз от препятствие, то при преобразовании расстояния пиксель будет иметь значение sqrt(4+9) = sqrt(13) в качестве значения пикселя. Таким образом, более темные пиксели обозначают близость к препятствиям, а более светлые значения означают, что они находятся далеко от препятствий.
Я хочу спланировать путь от заданного начального до целевого пикселя, используя информацию, предоставленную этим преобразованием расстояния, и оптимизировать стоимость пути, а также есть еще одно ограничение, что путь никогда не должен достигать пикселя, который меньше "х" пикселей. от препятствия.
Как мне это сделать?
PS Немного описания алгоритма (или немного кода) было бы полезно, так как я новичок в планировании алгоритмов.
3 ответа
Я нашел алгоритм в приложении I главы под названием
Джарвис, Рэй. Планирование пути на основе преобразования расстояний для навигации робота. Последние тенденции в мобильных роботах, 1993, 11: 3-31.
Эта глава полностью видна мне в книгах Google, и книга
ZHENG, Yuang F. (ed.). Последние тенденции в мобильных роботах. World Scientific, 1993.
Реализация алгоритма на C++ выглядит следующим образом:
#include <vector>
#include <iostream>
#include <cmath>
#include <algorithm>
#include <cassert>
#include <sstream>
/**
Algorithm in the appendix I of the chapter titled
JARVIS, Ray. Distance transform based path planning for robot navigation. *Recent trends in mobile robots*, 1993, 11: 3-31.
in the book
ZHENG, Yuang F. (ed.). *Recent trends in mobile robots*. World Scientific, 1993.
See also http://stackru.com/questions/21215244/least-cost-path-using-a-given-distance-transform
*/
template < class T >
class Matrix
{
private:
int m_width;
int m_height;
std::vector<T> m_data;
public:
Matrix(int width, int height) :
m_width(width), m_height(height), m_data(width *height) {}
int width() const
{
return m_width;
}
int height() const
{
return m_height;
}
void set(int x, int y, const T &value)
{
m_data[x + y * m_width] = value;
}
const T &get(int x, int y) const
{
return m_data[x + y * m_width];
}
};
float distance( const Matrix< float > &a, const Matrix< float > &b )
{
assert(a.width() == b.width());
assert(a.height() == b.height());
float r = 0;
for ( int y = 0; y < a.height(); y++ )
{
for ( int x = 0; x < a.width(); x++ )
{
r += fabs(a.get(x, y) - b.get(x, y));
}
}
return r;
}
int PPMGammaEncode(float radiance, float d)
{
//return int(std::pow(std::min(1.0f, std::max(0.0f, radiance * d)),1.0f / 2.2f) * 255.0f);
return radiance;
}
void PPM_image_save(const Matrix<float> &img, const std::string &filename, float d = 15.0f)
{
FILE *file = fopen(filename.c_str(), "wt");
const int m_width = img.width();
const int m_height = img.height();
fprintf(file, "P3 %d %d 255\n", m_width, m_height);
for (int y = 0; y < m_height; ++y)
{
fprintf(file, "\n# y = %d\n", y);
for (int x = 0; x < m_width; ++x)
{
const float &c(img.get(x, y));
fprintf(file, "%d %d %d\n",
PPMGammaEncode(c, d),
PPMGammaEncode(c, d),
PPMGammaEncode(c, d));
}
}
fclose(file);
}
void PPM_image_save(const Matrix<bool> &img, const std::string &filename, float d = 15.0f)
{
FILE *file = fopen(filename.c_str(), "wt");
const int m_width = img.width();
const int m_height = img.height();
fprintf(file, "P3 %d %d 255\n", m_width, m_height);
for (int y = 0; y < m_height; ++y)
{
fprintf(file, "\n# y = %d\n", y);
for (int x = 0; x < m_width; ++x)
{
float v = img.get(x, y) ? 255 : 0;
fprintf(file, "%d %d %d\n",
PPMGammaEncode(v, d),
PPMGammaEncode(v, d),
PPMGammaEncode(v, d));
}
}
fclose(file);
}
void add_obstacles(Matrix<bool> &m, int n, int avg_lenght, int sd_lenght)
{
int side = std::max(3, std::min(m.width(), m.height()) / 10);
for ( int y = m.height() / 2 - side / 2; y < m.height() / 2 + side / 2; y++ )
{
for ( int x = m.width() / 2 - side / 2; x < m.width() / 2 + side / 2; x++ )
{
m.set(x, y, true);
}
}
/*
for ( int y = m.height()/2-side/2; y < m.height()/2+side/2; y++ ) {
for ( int x = 0; x < m.width()/2+side; x++ ) {
m.set(x,y,true);
}
}
*/
for ( int y = 0; y < m.height(); y++ )
{
m.set(0, y, true);
m.set(m.width() - 1, y, true);
}
for ( int x = 0; x < m.width(); x++ )
{
m.set(x, 0, true);
m.set(x, m.height() - 1, true);
}
}
class Info
{
public:
Info() {}
Info(float v, int x_o, int y_o): value(v), x_offset(x_o), y_offset(y_o) {}
float value;
int x_offset;
int y_offset;
bool operator<(const Info &rhs) const
{
return value < rhs.value;
}
};
void next(const Matrix<float> &m, const int &x, const int &y, int &x_n, int &y_n)
{
//todo: choose the diagonal adiacent in case of ties.
x_n = x;
y_n = y;
Info neighbours[8];
neighbours[0] = Info(m.get(x - 1, y - 1), -1, -1);
neighbours[1] = Info(m.get(x , y - 1), 0, -1);
neighbours[2] = Info(m.get(x + 1, y - 1), +1, -1);
neighbours[3] = Info(m.get(x - 1, y ), -1, 0);
neighbours[4] = Info(m.get(x + 1, y ), +1, 0);
neighbours[5] = Info(m.get(x - 1, y + 1), -1, +1);
neighbours[6] = Info(m.get(x , y + 1), 0, +1);
neighbours[7] = Info(m.get(x + 1, y + 1), +1, +1);
auto the_min = *std::min_element(neighbours, neighbours + 8);
x_n += the_min.x_offset;
y_n += the_min.y_offset;
}
int main(int, char **)
{
std::size_t xMax = 200;
std::size_t yMax = 150;
Matrix<float> cell(xMax + 2, yMax + 2);
Matrix<bool> start(xMax + 2, yMax + 2);
start.set(0.1 * xMax, 0.1 * yMax, true);
Matrix<bool> goal(xMax + 2, yMax + 2);
goal.set(0.9 * xMax, 0.9 * yMax, true);
Matrix<bool> blocked(xMax + 2, yMax + 2);
add_obstacles(blocked, 1, 1, 1);
PPM_image_save(blocked, "blocked.ppm");
PPM_image_save(start, "start.ppm");
PPM_image_save(goal, "goal.ppm");
for ( int y = 0; y <= yMax + 1; y++ )
{
for ( int x = 0; x <= xMax + 1; x++ )
{
if ( goal.get(x, y) )
{
cell.set(x, y, 0.);
}
else
{
cell.set(x, y, xMax * yMax);
}
}
}
Matrix<float> previous_cell = cell;
float values[5];
int cnt = 0;
do
{
std::ostringstream oss;
oss << "cell_" << cnt++ << ".ppm";
PPM_image_save(cell, oss.str());
previous_cell = cell;
for ( int y = 2; y <= yMax; y++ )
{
for ( int x = 2; x <= xMax; x++ )
{
if (!blocked.get(x, y))
{
values[0] = cell.get(x - 1, y ) + 1;
values[1] = cell.get(x - 1, y - 1) + 1;
values[2] = cell.get(x , y - 1) + 1;
values[3] = cell.get(x + 1, y - 1) + 1;
values[4] = cell.get(x , y );
cell.set(x, y, *std::min_element(values, values + 5));
}
}
}
for ( int y = yMax - 1; y >= 1; y-- )
{
for ( int x = xMax - 1; x >= 1; x-- )
{
if (!blocked.get(x, y))
{
values[0] = cell.get(x + 1, y ) + 1;
values[1] = cell.get(x + 1, y + 1) + 1;
values[2] = cell.get(x , y + 1) + 1;
values[3] = cell.get(x - 1, y + 1) + 1;
values[4] = cell.get(x , y );
cell.set(x, y, *std::min_element(values, values + 5));
}
}
}
}
while (distance(previous_cell, cell) > 0.);
PPM_image_save(cell, "cell.ppm");
Matrix<bool> path(xMax + 2, yMax + 2);
for ( int y_s = 1; y_s <= yMax; y_s++ )
{
for ( int x_s = 1; x_s <= xMax; x_s++ )
{
if ( start.get(x_s, y_s) )
{
int x = x_s;
int y = y_s;
while (!goal.get(x, y))
{
path.set(x, y, true);
int x_n, y_n;
next(cell, x, y, x_n, y_n);
x = x_n;
y = y_n;
}
}
}
}
PPM_image_save(path, "path.ppm");
return 0;
}
Алгоритм использует простой формат изображения PPM, описанный, например, в главе 15 из книги " Компьютерная графика: принципы и практика - третье издание " Хьюза и др. для того, чтобы сохранить изображения.
Алгоритм начинается с изображения препятствий (blocked) и вычисляет из него преобразование расстояния (cell); затем, начиная с преобразования расстояния, он вычисляет оптимальный путь с использованием метода наискорейшего спуска: он спускается вниз в поле потенциала расстояния преобразования. Таким образом, вы можете начать с вашего собственного изображения трансформации расстояния.
Обратите внимание, что мне кажется, что алгоритм не удовлетворяет вашему дополнительному ограничению, которое:
путь никогда не должен достигать пикселя, который находится на расстоянии менее x пикселей от препятствия.
На следующем изображении png изображено препятствие, сгенерированное программой blocked.ppm изображение было экспортировано в формате png через Gimp:

Следующее изображение в формате png является изображением начальной точки, сгенерированной программой start.ppm изображение было экспортировано в формате png через Gimp:

Следующее изображение png является изображением конечной точки, сгенерированной программой goal.ppm изображение было экспортировано в формате png через Gimp:

Следующее изображение png является изображением вычисленного пути, сгенерированной программой path.ppm изображение было экспортировано в формате png через Gimp:
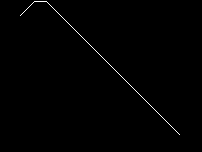
Следующее изображение в формате png является изображением трансформации расстояния, сгенерированной программой cell.ppm изображение было экспортировано в формате png через Gimp:

Я нашел статью Джарвиса, посмотрев на
CHIN, Yew Tuck, et al. Vision Guided Ag v с использованием трансформации расстояния. В кн.: Материалы 32-го ISR (Международный симпозиум по робототехнике). 2001. с. 21.
Обновить:
Алгоритм Джарвиса рассмотрен в следующей статье, где авторы утверждают, что:
Поскольку путь находится путем локального выбора только между соседними ячейками, полученный путь может быть субоптимальным
ЭЛИЗОНДО-ЛИЛ, Хуан Карлос; ПАРРА-ГОНСАЛЕС, Эзра Федерико; Рамирес-Торрес, Хосе Габриэль. Точное евклидово преобразование расстояний: новый алгоритм для универсального планирования пути. Int J Adv Robotic Sy, 2013, 10.266.
На карте пикселей с преобразованием расстояния вы выбираете начальный пиксель, а затем выбираете его соседа с меньшим значением, чем у исходного пикселя - повторяйте процесс до тех пор, пока не будет достигнут целевой пиксель (пиксель со значением ноль).
Обычно целевой пиксель имеет значение ноль, наименьшее число из всех пройденных режимов.
Проблема не проходить близко к барьерам является серебряной, генерируя карту преобразования расстояния, чтобы барьеры были увеличены. Например, если вы хотите сделать интервал в два пикселя для любого барьера - просто добавьте два пикселя значения барьера. Обычно барьеры, которые не могут быть пройдены, получают значение минус один. То же значение, которое я использовал для краев. Альтернативный подход заключается в том, чтобы окружить барьеры с очень высокой стартовой ценностью - путь не гарантированно приближается, но алгоритм будет пытаться избегать путей в непосредственной близости от барьеров.
Для решения на основе графиков вы можете проверить, например, главу 15 книги
DE BERG, Mark et al. Вычислительная геометрия. Springer Berlin Heidelberg, 2008.
которая имеет название "Графики видимости - поиск кратчайшего маршрута" и находится в свободном доступе на сайте издателя.
Глава объясняет, как вычислить евклидов кратчайший путь, начиная с так называемого графа видимости. График видимости рассчитывается, исходя из набора препятствий, каждое препятствие описывается как многоугольник.
Евклидов кратчайший путь затем находит, применяя алгоритм кратчайшего пути, такой как алгоритм Дейкстры, к графу видимости.
В вашем изображении с преобразованием расстояния препятствия представлены пикселями с нулевым значением, поэтому вы можете попытаться аппроксимировать их как многоугольники, а затем применить метод, описанный в цитированной книге.