Перерисовать изображение с 3D-перспективы на 2D

Question

Мне нужно обратное преобразование перспективы, написанное на Паскале /Delphi/Lazarus. Смотрите следующее изображение:

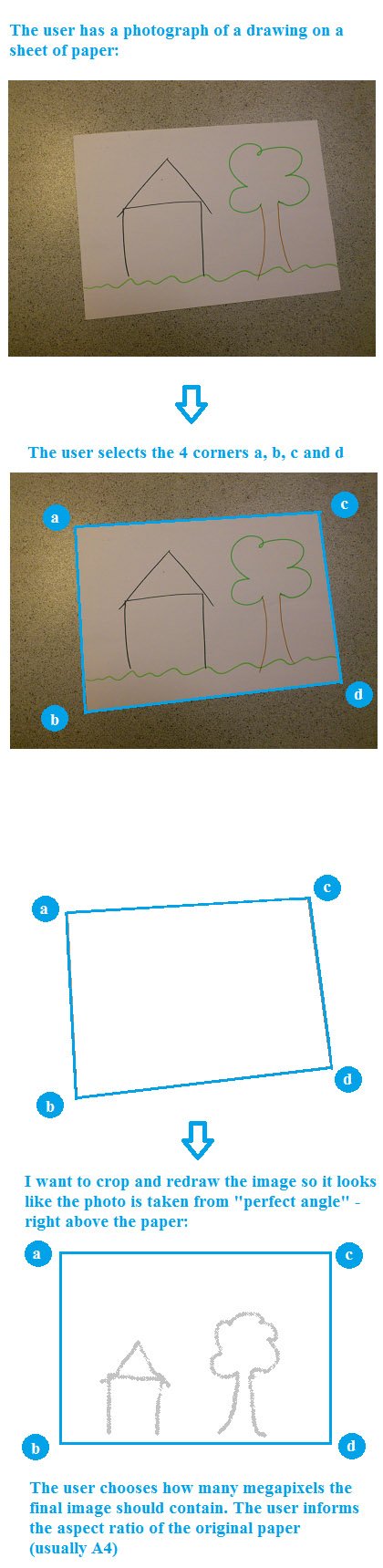
Я думаю, что мне нужно пройти через целевые пиксели, а затем рассчитать соответствующую позицию в исходном изображении (чтобы избежать проблем с ошибками округления и т. Д.).

function redraw_3d_to_2d(sourcebitmap:tbitmap, sourceaspect:extended, point_a, point_b, point_c, point_d:tpoint, megapixelcount:integer):tbitmap;
var
   destinationbitmap:tbitmap;
   x,y,sx,sy:integer;
begin
  destinationbitmap:=tbitmap.create;
  destinationbitmap.width=megapixelcount*sourceaspect*???; // I dont how to calculate this
  destinationbitmap.height=megapixelcount*sourceaspect*???; // I dont how to calculate this
  for x:=0 to destinationbitmap.width-1 do
    for y:=0 to destinationbitmap.height-1 do
    begin
        sx:=??;
        sy:=??;
        destinationbitmap.canvas.pixels[x,y]=sourcebitmap.canvas.pixels[sx,sy];
    end;
  result:=destinationbitmap;
end;

Мне нужна настоящая формула... Так что решение OpenGL не было бы идеальным...

Answer 1

Примечание: есть версия этого с правильной математической версткой на Math SE.

Вычисление проективного преобразования

Перспектива является частным случаем проективного преобразования, которое, в свою очередь, определяется четырьмя точками.

Шаг 1: Начиная с 4 позиций в исходном изображении с именем (x1,y1) через (x4,y4)Вы решаете следующую систему линейных уравнений:

[x1 x2 x3] [λ]   [x4]
[y1 y2 y3]∙[μ] = [y4]
[ 1  1  1] [τ]   [ 1]

Столбцы образуют однородные координаты: еще одно измерение, созданное путем добавления 1 как последняя запись. На последующих этапах кратные значения этих векторов будут использоваться для обозначения одинаковых точек. Смотрите последний шаг для примера того, как превратить их обратно в двумерные координаты.

Шаг 2: Масштабируйте столбцы по коэффициентам, которые вы только что вычислили:

    [λ∙x1 μ∙x2 τ∙x3]
A = [λ∙y1 μ∙y2 τ∙y3]
    [λ    μ    τ   ]

Эта матрица будет отображаться (1,0,0) к кратному (x1,y1,1), (0,1,0) к кратному (x2,y2,1), (0,0,1) к кратному (x3,y3,1) а также (1,1,1) в (x4,y4,1), Таким образом, он отобразит эти четыре специальных вектора (называемые базисными векторами в последующих объяснениях) в указанные позиции на изображении.

Шаг 3: Повторите шаги 1 и 2 для соответствующих позиций в целевом изображении, чтобы получить вторую матрицу под названием B,

Это карта от базовых векторов до конечных позиций.

Шаг 4: инвертировать B чтобы получить B⁻¹,

B сопоставляет базисные векторы с позициями назначения, поэтому обратная матрица отображается в обратном направлении.

Шаг 5: Вычислить объединенную матрицу C = A∙B⁻¹,

B⁻¹ карты от позиций назначения до базисных векторов, в то время как A карты оттуда к исходным позициям. Таким образом, комбинация отображает конечные позиции на исходные позиции.

Шаг 6: для каждого пикселя (x,y) целевого изображения, рассчитать произведение

[x']     [x]
[y'] = C∙[y]
[z']     [1]

Это однородные координаты вашей преобразованной точки.

Шаг 7: Вычислите позицию в исходном изображении следующим образом:

sx = x'/z'
sy = y'/z'

Это называется дегомогенизацией координатного вектора.

Вся эта математика была бы намного легче читать и писать, если бы SO поддерживал MathJax… ☹

Выбор размера изображения

Вышеуказанный подход предполагает, что вы знаете расположение ваших углов на изображении назначения. Для этого вы должны знать ширину и высоту этого изображения, которое также отмечено знаками вопроса в вашем коде. Итак, давайте предположим, height вашего выходного изображения были 1и width мы sourceaspect, В этом случае общая площадь будет sourceaspect также. Вы должны масштабировать эту область с коэффициентом pixelcount/sourceaspect достичь области pixelcount, Это означает, что вы должны масштабировать каждую длину ребра по квадратному корню из этого фактора. Итак, в конце концов, у вас есть

pixelcount = 1000000.*megapixelcount;
width  = round(sqrt(pixelcount*sourceaspect));
height = round(sqrt(pixelcount/sourceaspect));

Answer 2

Используйте Graphics32, в частности TProjectiveTransformation (для использования с методом Transform). Не забудьте оставить прозрачное поле на исходном изображении, чтобы не было неровных краев.