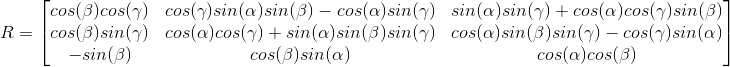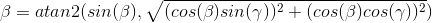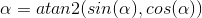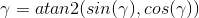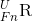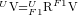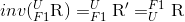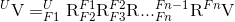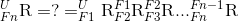Разлагающая матрица вращения (x,y',z'') - декартовы углы
Разлагающая матрица вращения (x,y',z'') - декартовы углы
В настоящее время я работаю с матрицами вращения, и у меня есть следующая проблема: учитывая три системы координат (O0,x0,y0,z0; O1,x1,y1,z1; O2,x2,y2,z2) которые совпадают. Сначала мы поворачиваем кадр № 1 относительно кадра № 0, затем кадр № 2 относительно кадра № 1.
Порядок вращений: R = Rx_alpha * Ry_beta * Rz_gammaИтак, сначала о x, затем y ', затем z' ', которые также известны как декартовы углы. Если R1 обозначает 1-й, а R2 - 2-й поворот, мы ищем углы 2-го кадра относительно исходного кадра (#0) после обоих вращений. Это можно сделать, разложив матрицу вращения R (где:R = R1*R2). Есть много доступной литературы, как это можно сделать с помощью углов Эйлера и RPY, но я не нахожу никакой, как решить эту проблему в случае декартовых углов.
У меня есть функция Matlab, которая работает только с помощью простых вращений. Если все углы имеют значения, отличные от 0 (пример ниже), то результат становится действительно нестабильным.
Ориентация 1-го кадра относительно кадра № 0:
alpha1 = 30*pi/180;
beta1 = 10*pi/180;
gamma1 = 0*pi/180;
Ориентация 2-го кадра относительно кадра № 1
alpha2 = 10*pi/180;
beta2 = 10*pi/180;
gamma2 = 0*pi/180;
Функция Matlab, которую я использовал для решения проблемы:
function [q] = cartesian_angles(R)
beta = asin(R(1,3));
*% Catching the numerical singularty*
if abs(abs(beta)-pi/2) > eps;
*% singulartiy of acos*
gamma1 = acos(R(1,1) / cos(beta));
gamma2 = asin(-R(1,2) / cos(beta));
if gamma2<0
gamma=2*pi-gamma1;
else
gamma=gamma1;
end
alpha1 = acos(R(3,3) / cos(beta));
alpha2 = asin(-R(2,3) / cos(beta));
if alpha2<0
alpha = 2*pi-alpha1;
else
alpha = alpha1;
end
else
fprintf('beta=pi/2 \n')
gamma = 0;
alpha = 0;
beta = 0;
end;
alpha = alpha*180/pi;
beta = beta*180/pi;
gamma = gamma*180/pi;
q = [alpha; beta; gamma];
Спасибо за любую помощь! Если у вас есть вопросы, не стесняйтесь спрашивать!
Марси
2 ответа
Во-первых, я собираюсь предположить, что вы передаете в свою функцию хорошо обусловленную правостороннюю матрицу вращения. Я собираюсь использовать ту же последовательность вращения, что вы перечислили выше, X Y' Z''
Если вы знаете символическую конструкцию матрицы вращения, из которой вы пытаетесь извлечь углы, математика довольно проста. Ниже приведен пример кода Matlab для определения построения матрицы вращения порядка X-Y'-Z''
a = sym('a');%x
b = sym('b');%y
g = sym('g');%z
Rx = [1 0 0;0 cos(a) -sin(a);0 sin(a) cos(a)];
Ry = [cos(b) 0 sin(b);0 1 0;-sin(b) 0 cos(b)];
Rz = [cos(g) -sin(g) 0;sin(g) cos(g) 0;0 0 1];
R = Rz*Ry*Rx
Вывод выглядит так:
R =
[ cos(b)*cos(g), cos(g)*sin(a)*sin(b) - cos(a)*sin(g), sin(a)*sin(g) + cos(a)*cos(g)*sin(b)]
[ cos(b)*sin(g), cos(a)*cos(g) + sin(a)*sin(b)*sin(g), cos(a)*sin(b)*sin(g) - cos(g)*sin(a)]
[ -sin(b), cos(b)*sin(a), cos(a)*cos(b)]
Вот тот же результат в более привлекательном формате:
Теперь давайте перейдем к математике, чтобы извлечь углы из этой матрицы. Сейчас самое время освоиться с функцией atan2().
Сначала определите угол бета (кстати, альфа - это вращение вокруг оси X, бета - это вращение вокруг оси Y, а гамма - это угол вокруг оси Z):
beta = atan2(-1*R(3,1),sqrt(R(1,1)^2+R(2,1)^2))
Написано более формально,
Теперь, когда мы определили для угла бета, мы можем решить проще для двух других углов:
alpha = atan2(R(3,2)/cos(beta),R(3,3)/cos(beta))
gamma = atan2(R(2,1)/cos(beta),R(1,1)/cos(beta))
Упрощенно и в более хорошем формате,
Приведенный выше метод является довольно надежным способом получения углов Эйлера из матрицы вращения. Функция atan2 действительно делает это намного проще.
Напоследок я отвечу, как решить для углов поворота после серии поворотов. Сначала рассмотрим следующие обозначения. Вектор или матрица вращения будут записываться следующим образом:
Здесь "U" представляет универсальный каркас или глобальную систему координат. "Fn" представляет n-ю локальную систему координат, которая отличается от U. R означает матрицу вращения (это обозначение также может использоваться для однородных преобразований). Верхний индекс слева всегда будет представлять родительскую систему отсчета матрицы вращения или вектора. Нижний индекс слева указывает на дочернюю систему отсчета. Например, если у меня есть вектор в F1, и я хочу знать, что он эквивалентен в универсальной системе координат, я бы выполнил следующую операцию:
Чтобы получить вектор, разрешенный в универсальном фрейме, я просто умножил его на матрицу вращения, которая преобразует вещи из F1 в U. Обратите внимание, как индексы "аннулируются" верхним индексом следующего элемента в уравнении. Это умная нотация, чтобы помочь кому-то запутаться. Если вы помните, специальным свойством хорошо обусловленных матриц вращения является то, что обратная матрица является транспонированной матрицей, которая также будет обратным преобразованием, подобным этому:
Теперь, когда детали обозначений не в порядке, мы можем начать рассматривать решение для сложных серий вращений. Допустим, у меня есть "n" количество координатных кадров (другой способ сказать "n" различных поворотов). Чтобы выяснить вектор в "n-ом" кадре в универсальном кадре, я бы сделал следующее:
Чтобы определить углы Кардана / Эйлера, которые возникают в результате "n" поворотов, вы уже знаете, как разложить матрицу, чтобы получить правильные углы (также известные как обратная кинематика в некоторых областях), вам просто нужна правильная матрица. В этом примере меня интересует матрица вращения, которая берет вещи в "n-й" системе координат и разрешает их в универсальную систему U:
Так вот, я объединил все повороты в интересующий, просто умножив их в правильном порядке. Этот пример был легким. Более сложные случаи возникают, когда кто-то хочет найти систему отсчета одного твердого тела, разрешенную в кадре другого, и единственное, что объединяет два твердых тела, - это их измерение в универсальной системе отсчета.
Хочу также отметить, что эти обозначения и метод также могут использоваться с однородными преобразованиями, но с некоторыми ключевыми отличиями. Обратная матрица вращения - это ее транспонирование, это не верно для однородных преобразований.
Спасибо за ваш ответ willpower2727, ваш ответ был действительно полезным!
Но я хотел бы отметить, что код, который вы показали, полезен для декомпозиции вращательных матриц, которые построены следующим образом:
R = Rz*Ry*Rx
Что я ищу:
R = Rx*Ry*Rz
В результате получается следующая матрица вращения:
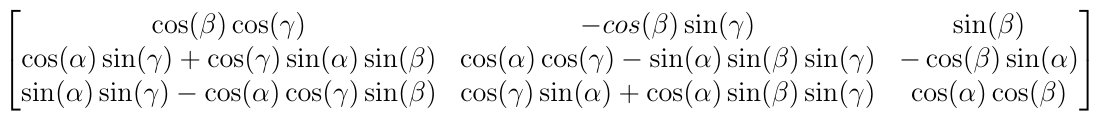
Однако это не проблема, поскольку, следуя методу расчета углов альфа, бета и гамма, было легко изменить код, чтобы он разложил матрицу, показанную выше.
Углы:
beta = atan2( R(1,3), sqrt(R(1,1)^2+(-R(1,2))^2) )
alpha = atan2( -(R(2,3)/cos(beta)),R(3,3)/cos(beta) )
gamma = atan2( -(R(1,2)/cos(beta)),R(1,1)/cos(beta) )
Одна вещь все еще не ясна все же. Метод совершенно полезен, но только если я вычисляю углы после одного поворота. Поскольку есть больше поворотов, связанных друг с другом, результаты ложны. Тем не менее, это все еще разрешимо, я думаю, учитывая следующий способ: допустим, у нас есть два поворота, связанных друг с другом (R1 и R2). q1 показывает углы R1, q2 R2. после разложения одиночных матриц. Общий угол поворота матрицы R=R1*R2может быть легко вычислено путем суммирования рангов до: q=q1+q2
Разве нет способа, как рассчитать углы полного вращения, не суммируя парциальные углы, а разложив матрицу R=R1*R2?
ОБНОВИТЬ:
Рассмотрим следующий базовый пример. Вращения связаны друг с другом:
a1 = 10*pi/180
b1 = 20*pi/180
g1 = 40*pi/180
R1 = Rx_a1*Ry_b1_Rz_g1
a2 = 20*pi/180
b2 = 30*pi/180
g2 = 30*pi/180
R2 = Rx_a2*Ry_b2*Rz_g2
Разложение отдельных матриц R1 и R2 приводит к углам прав. Проблема возникает, когда я связываю вращения друг с другом и пытаюсь определить углы последнего кадра в инерциальном кадре. Теоретически это можно сделать, разложив произведение всех вращательных матриц цепочки преобразований.
R = R1*R2
Разложение этой матрицы дает следующий ложный результат, показанный в градусах:
a = 0.5645
b = 54.8024
g = 61.4240
Марси