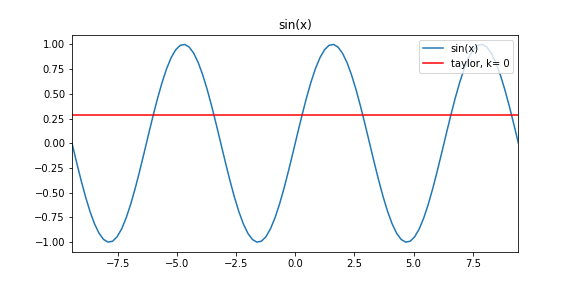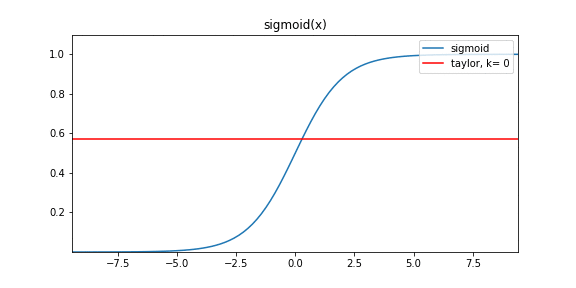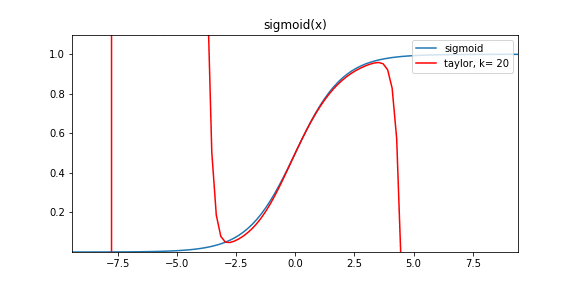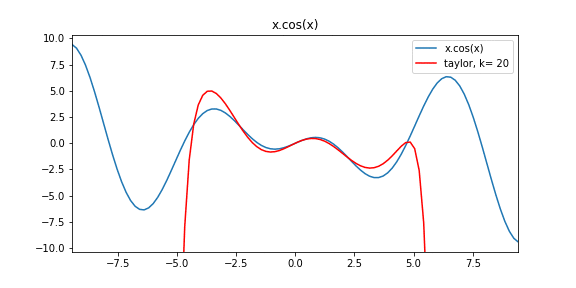
Расширение Тейлора для данного набора данных без функциональной формы

Question

У меня есть (x,y) набор данных, который является непрерывным и дифференцируемым. Точная функциональная форма не известна. Я хочу Тейлор расширить график в какой-то момент. Я попытался с помощью algopy/Adipy. Проблема в том, что они требуют функциональной формы.

Я прилагаю пример кода algopy.

 import numpy; from numpy import sin,cos
 from algopy import UTPM

 def f(x):
     return sin(cos(x) + sin(x))

D = 100; P = 1
x = UTPM(numpy.zeros((D,P)))
x.data[0,0] = 0.3
x.data[1,0] = 1
y = f(x)
print('coefficients of y =', y.data[:,0])

где D - порядок многочлена.

Я попытался использовать следующее (x1 и y1 являются одномерными массивами):

from scipy.interpolate import interp1d
f1 = interp1d(x1, y1, kind='cubic')
def f(x):
    temp1=f1(x)
    return np.float64(temp1)

Однако интерполяция, по-видимому, не принимает тип данных x, возвращаемый UTPM.

Сообщение об ошибке:

Traceback (most recent call last):
      File "tay.py", line 26, in <module>
        y = f(x)
      File "tay.py", line 15, in f
        temp1=f1(x)
      File "/usr/lib/python2.7/dist-packages/scipy/interpolate/polyint.py", line 54, in __call__
        y = self._evaluate(x)
      File "/usr/lib/python2.7/dist-packages/scipy/interpolate/interpolate.py", line 449, in _evaluate
        y_new = self._call(self, x_new)
      File "/usr/lib/python2.7/dist-packages/scipy/interpolate/interpolate.py", line 441, in _call_spline
        return spleval(self._spline, x_new)
      File "/usr/lib/python2.7/dist-packages/scipy/interpolate/interpolate.py", line 919, in spleval
        res[sl] = _fitpack._bspleval(xx,xj,cvals[sl],k,deriv)
    TypeError: Cannot cast array data from dtype('O') to dtype('float64') according to the rule 'safe'

Answer 1

Я искал то же самое, поэтому я реализовал это:

import numpy as np
import matplotlib.pyplot as plt
from math import factorial as f

def dxdy(x,y,order): 
    dy = y
    for k  in range(order+1):
        print(k)
        dx = (x[-1]-x[0])/len(x)
        if k == 1:
            dy = y
        elif k % 2 == 0:
            dy = (dy[1:]-dy[:-1])/dx
            x = x[:-1]       
        elif k % 2 != 0:
            dy = (dy[1:]-dy[:-1])/dx
            x = x[1:]
    return dy

def taylor(x,y,n):
    a = x[int(len(x)/2)+1]
    center = int(len(x)/2)+1o
    #plt.plot(y)
    #plt.ylim(min(y),max(y))
    for k in range(n+1):
        print(k)
        if k == 0:
            y_hat = (y[center]*((x-a)**k))/f(k)
            #plt.plot(y_hat)
        else:
            y_hat += (dxdy(x,y,k+1)[center]*((x-a)**k))/f(k)
            #plt.plot(y_hat)
        #plt.plot(y)
    return y_hat

points = 101
x = np.linspace(-3*np.pi,3*np.pi,points)
y = 1/(1+np.exp(-x))
y = np.cos(x)#*x#(x**4)
center = int(points/2)
for k in range(21):
    y_hat = taylor(x,y,k)
    plt.figure(figsize=(8,4))
    plt.ylim(min(y)*1.1,max(y)*1.1)
    plt.xlim(min(x),max(x))
    plt.plot(x,y)
    plt.plot(x,y_hat,c='red')
    plt.legend(['cs(x)','taylor, k= '+str(k)],loc='upper right')
    plt.title('cos(x)') 
    plt.savefig('cos'+str(k)+'.png')

Answer 2

Выполнение разложения Тейлора набора данных, определенного в дискретных точках, не имеет смысла. В частности, следующее предположение неверно,

У меня есть (x,y) набор данных, который является непрерывным и дифференцируемым. Точная функциональная форма не известна.

Вы можете иметь только непрерывную функцию, если вы связываете некоторую процедуру интерполяции с вашим набором данных, но тогда это также исправит общую функциональную форму.

Например, скажем, мы используем кусочно-кубическую интерполяцию, как в вопросе. Это означает, что разложение Тейлора будет эффективно ограничено коэффициентами кубического полинома, использованного для интерполяции (и может быть не более 3-го порядка). Кроме того, другая процедура интерполяции даст другое расширение Тейлора.

В целом, результаты будут в основном зависеть от процедуры интерполяции, а не от ваших данных. Это связано с тем, что расширение Тейлора основано на локальном поведении функции, которого нет в вашем наборе данных (x,y).

Вместо этого вы можете локально подогнать свои данные полиномом некоторого порядка, что даст эквивалент расширения Тейлора для выборочных данных.