OpenGL понимают две точки зрения, чтобы увидеть преобразование модели
Есть две точки зрения, чтобы понять преобразования модели, я прочитал из Красной книги 7-е издание,[Великий, Фиксированная система координат ] и [Перемещение локальной системы координат ].
Мой вопрос:
В чем разница между двумя точками зрения и когда их использовать в определенной ситуации?
дополнительная контекстная информация:
Я хотел бы дать вам некоторый контекст, чтобы помочь мне, или вы можете просто проигнорировать ниже детали.
Я понял эти две точки зрения следующим образом. Думаю, у меня есть следующий код: (такие функции, как glTranslatef, устарели, заменены библиотекой математики, но теория может помочь.)
//render the sence,and use orthogonal projection
void display( void )
{
glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
drawAixs(4.8f);//draw x y z aixs,4.8 is axis length
glRotatef(45.0,0.0,0.0,1.0);
glTranslatef(3.0,0.0,0.0);
glutSolidCube(2.0);
glutSwapBuffers();
}
Из локального координатного представления:
С этой точки зрения мы можем понять это следующим образом:
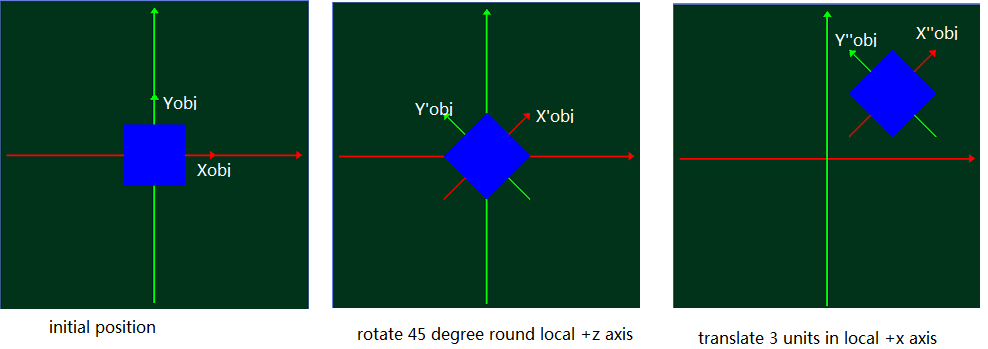
И текущая матрица преобразования (CTM):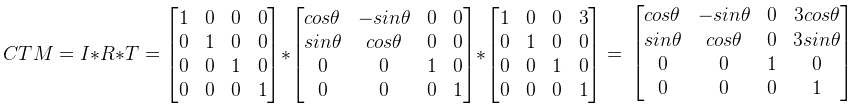
Из глобального представления с фиксированными координатами:
С этой точки зрения мы можем получить:
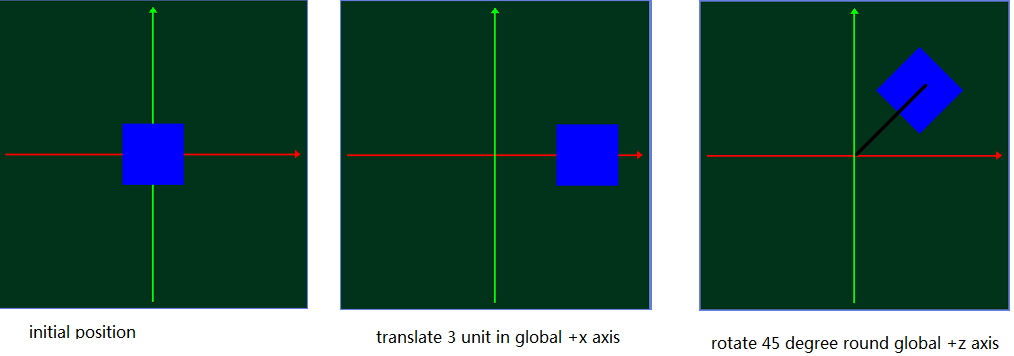
1 ответ
Две системы координат - это просто соглашение. Всегда существует одна глобальная система координат, но может быть много локальных систем. Понятие локальной системы - это всего лишь соглашение. Общая матрица преобразований M трансформирует вершины из одного пространства в другое:
v' = M * v
Чтобы v находится в одном координатном пространстве и v' находится в другом. В случае M описывает положение объекта, мы говорим, что он помещает вершины из локальной системы координат объекта в систему координат глобального мира. С другой стороны, если он описывает положение и проекцию камеры, он помещает вершины из мировой системы координат в другую локальную систему координат глаза.
Сложные объекты с суставами (например, гуманоидные персонажи или механизмы с шарнирами) могут фактически иметь несколько промежуточных локальных пространств, где преобразования связаны в цепочку, в зависимости от структуры скелета объекта.
Обычно один использует object space где вершины моделей определены, world space который является глобальным пространством, где координаты могут быть связаны друг с другом, и camera space или же eye space что пространство экранных координат. Но с появлением шейдеров OpenGL 3 это совершенно произвольно: вы можете написать свой шейдер так, чтобы он использовал единственную матрицу, которая преобразует вершины из пространства объектов непосредственно в пространство экрана. Поэтому не беспокойтесь о координатных кадрах, просто сосредоточьтесь на поставленной задаче - что именно вы хотите отобразить и как объекты должны двигаться (относительно друг друга или относительно некоторой общей ссылки).