Python curve_fit с измеренными точками данных

Question

Я измерил точки данных, я хочу соответствовать формуле для определения двух объектов. Однако я получаю ошибку:

TypeError: ufunc 'bitwise_xor' не поддерживается для типов ввода, и входы не могут быть безопасно приведены к любым поддерживаемым типам в соответствии с правилом приведения "safe"

производится с помощью следующего кода Python (я использую версию 3):

 import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

def func(T, fun, Tc):
    return fun*np.sqrt(np.cos(np.pi/2*(T/Tc)^2))

xdata=(4.61, 4.89, 4.92, 4.95, 5.06, 5.10, 5.21, 5.38, 5.41, 5.57, 5.80, 6.14, 6.61, 7.27, 7.66, 7.90, 8.91, 8.29, 8.23, 7.30, 7.86,
       8.30, 8.89, 8.99, 9.24, 9.35, 9.50, 8.77, 8.27, 8.37, 7.72, 7.57, 7.99, 8.13) # these are temperature values <-> T

ydata=(2.85, 2.84, 2.83, 2.825, 2.82, 2.81, 2.80, 2.765, 2.76, 2.74, 2.695, 2.62, 2.50, 2.265, 2.105, 1.975, 1.23, 1.75, 1.81, 2.26,
       2.005, 1.75, 1.31, 1.14, 1.015, 1.045, 1.06, 1.40, 1.75, 1.69, 2.075, 2.15, 1.93, 1.855) # these are energy values <-> func

popt, pcov = curve_fit(func, xdata, ydata)
popt #display these optimized values

Здесь прибывает вышеупомянутая ошибка!!!

Я нашел способ сделать это, если у вас есть фиксированная формула и добавить немного шума, но я измерил точки данных (они должны быть дискретными).

Спасибо! Карстен

Answer 1

Я думаю, что большая часть ошибки, которую вы видите, заключается в том, что вы не указали начальные значения для подходящих переменных fun а также Tc, К сожалению, Сципи curve_fit() позволяет это и молча присваивает значениям 1.0, что поощряет плохую практику и является очень плохой "функцией". Не используйте это.

Позвольте мне порекомендовать lmfit ( https://lmfit.github.io/lmfit-py), который предоставляет интерфейс более высокого уровня для подбора кривой, который проще в использовании, лучше избегает плохого поведения и имеет множество полезных функций, недоступных при curve_fit(),

С lmfit ваша проблема подгонки будет выглядеть так (для ясности я изменил несколько имен переменных):

import numpy as np
import matplotlib.pyplot as plt
from lmfit import Model

def func(t, scale, tc):
    return scale*np.sqrt(np.cos(np.pi/2*(t/tc)**2))

tdata = np.array([4.61, 4.89, 4.92, 4.95, 5.06, 5.10, 5.21, 5.38, 5.41, 5.57, 5.80, 6.14, 6.61, 7.27, 7.66, 7.90, 8.91, 8.29, 8.23, 7.30, 7.86,
                  8.30, 8.89, 8.99, 9.24, 9.35, 9.50, 8.77, 8.27, 8.37, 7.72, 7.57, 7.99, 8.13]) # these are temperature values <-> T

energy = np.array([2.85, 2.84, 2.83, 2.825, 2.82, 2.81, 2.80, 2.765, 2.76, 2.74, 2.695, 2.62, 2.50, 2.265, 2.105, 1.975, 1.23, 1.75, 1.81, 2.26,
                   2.005, 1.75, 1.31, 1.14, 1.015, 1.045, 1.06, 1.40, 1.75, 1.69, 2.075, 2.15, 1.93, 1.855]) # these are energy values <-> func

fmodel = Model(func)

params = fmodel.make_params(scale=5, tc=10)

result = fmodel.fit(energy, params, t=tdata)
print(result.fit_report())

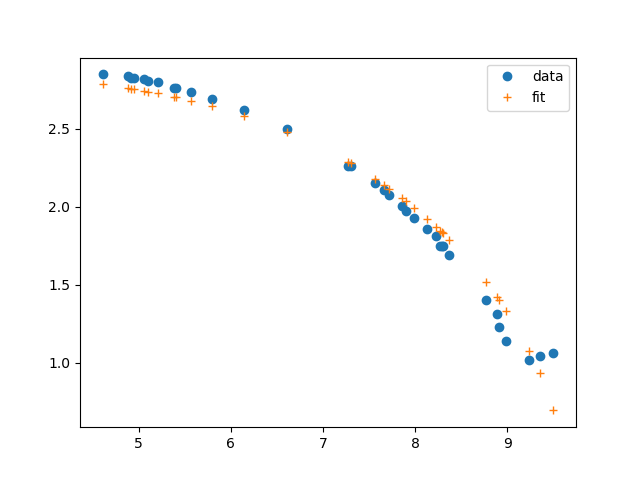
plt.plot(tdata, energy, 'o', label='data')
plt.plot(tdata, result.best_fit, '+', label='fit')

plt.legend()
plt.show()

который распечатает отчет

[[Model]]
    Model(func)
[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 24
    # data points      = 34
    # variables        = 2
    chi-square         = 0.34988407
    reduced chi-square = 0.01093388
    Akaike info crit   = -151.601474
    Bayesian info crit = -148.548753
[[Variables]]
    scale:  2.87776739 +/- 0.02737439 (0.95%) (init = 5)
    tc:     9.68051725 +/- 0.03597889 (0.37%) (init = 10)
[[Correlations]] (unreported correlations are < 0.100)
    C(scale, tc) = -0.506

и создать график, как