Генерация идеально нормально распределенной выборки размером n в R

Question

Я хотел бы сгенерировать выборку со средним значением = 0, sd = 1 и размером n = 100, распределение которого является нормальным, насколько это возможно. Использование rnorm само по себе возвращает большую изменчивость.

Единственный способ, который я нашел, - усреднить несколько норм.

rowMeans(replicate(10000, sort(rnorm(100, 0, 1))))

Это возвращает довольно удовлетворительный результат, но я не уверен, что это самый эффективный способ сделать это.

---

РЕДАКТИРОВАТЬ:

Я не хочу, чтобы среднее значение и sd были строго равны 0 и 1, а скорее, чтобы распределение выглядело как нормальное распределение (при построении кривой плотности).

Кажется, что метод qnorm работает хуже, чем "средний" метод:

# qnorm method
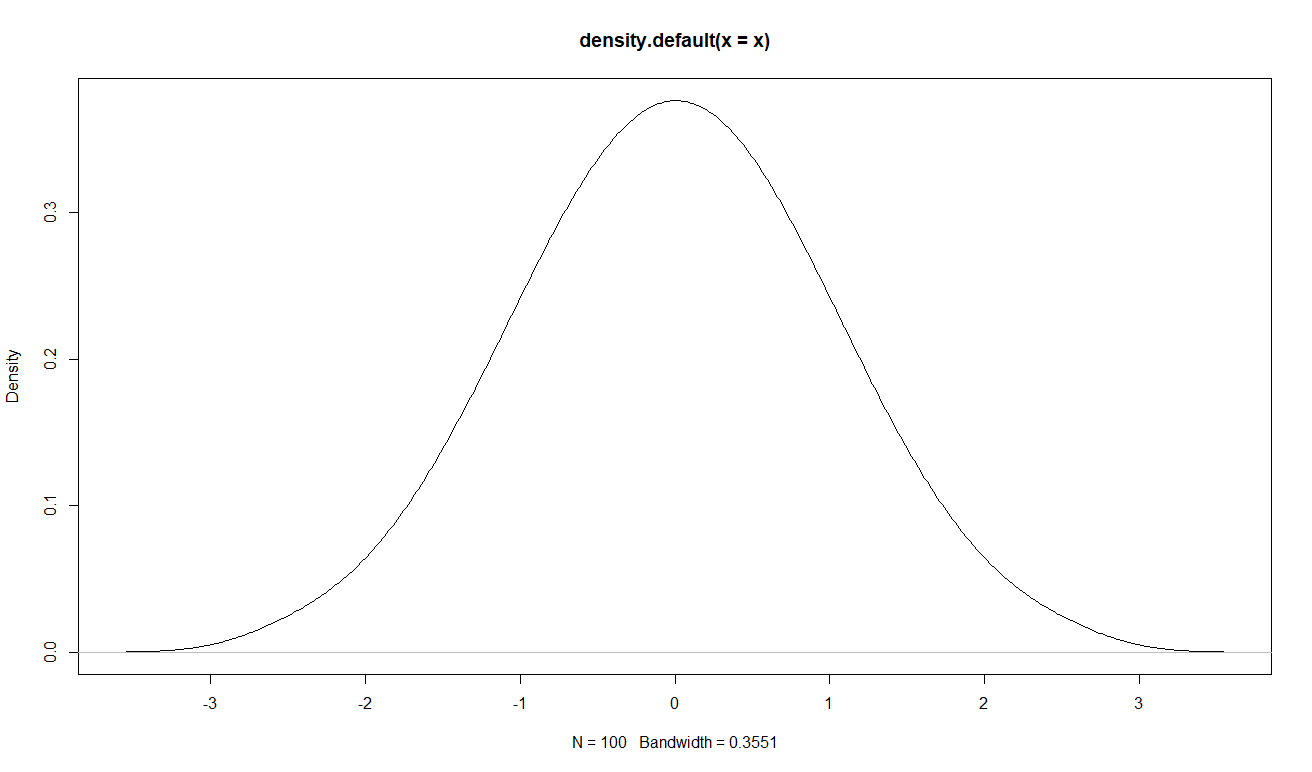
x <- qnorm(seq(.00001, .99999, length.out = 100), mean=0, sd=1)
plot(density(x))

# average method
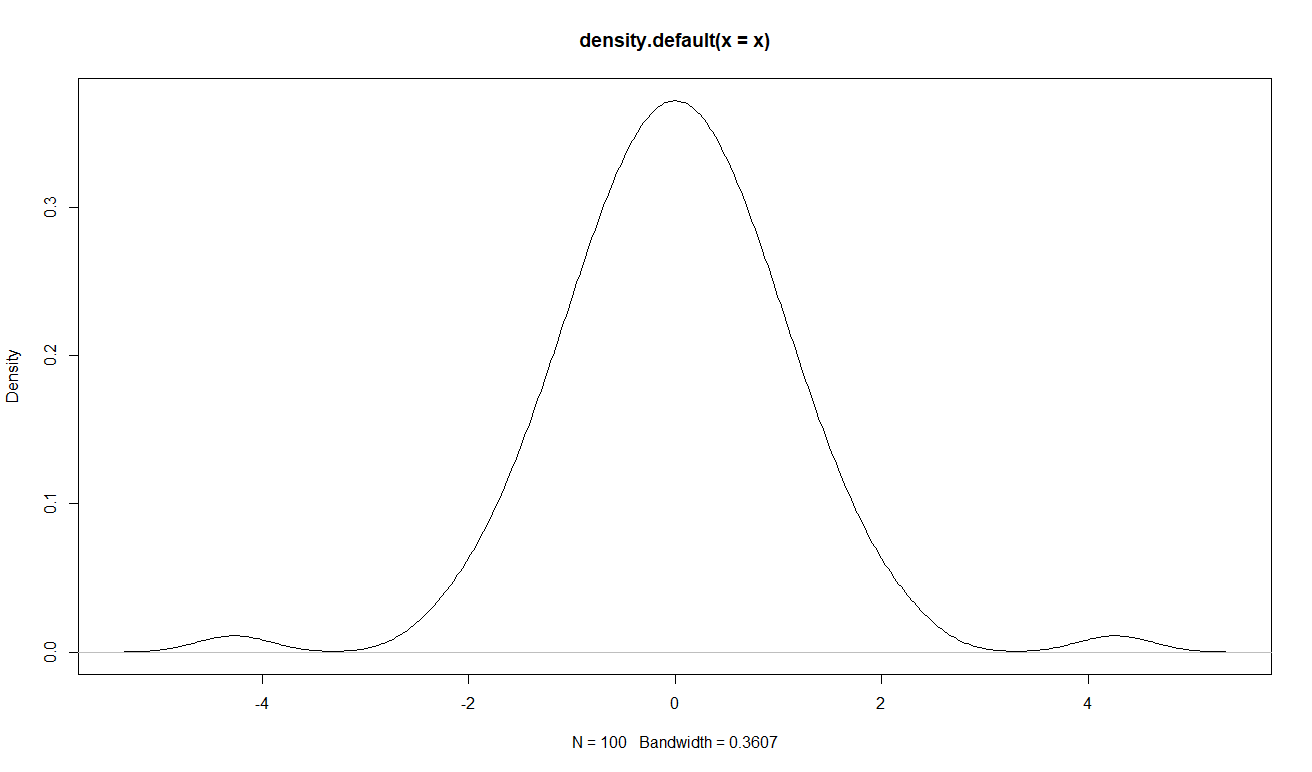
x <- rowMeans(replicate(10000, sort(rnorm(100, mean=0, sd=1))))
plot(density(x))

Я был бы доволен детерминированным решением, возвращающим результаты, близкие к среднему, более эффективным способом.

---

РЕДАКТИРОВАТЬ 2: Возможное решение

Основываясь на ответах, кажется, что работает следующее, корректируя границы относительно n:

x <- qnorm(seq(1/n, 1-1/n, length.out = n), mean=0, sd=1)

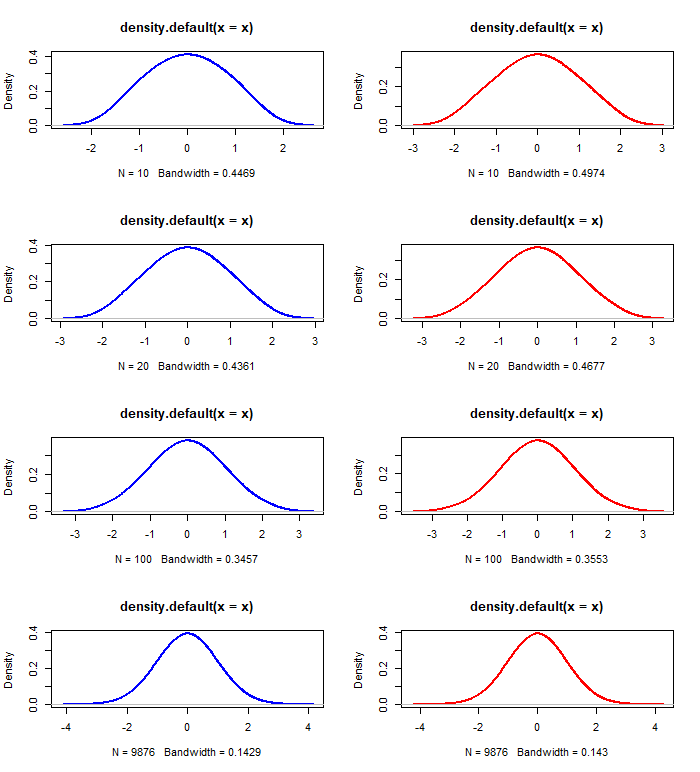
Ниже приведено сравнение методов qnorm и среднего для разных значений n:

par(mfrow=c(6,2))
for(n in c(10, 20, 100, 500, 1000, 9876)){
  x <- qnorm(seq(1/n, 1-1/n, length.out = n), mean=0, sd=1)
  plot(density(x), col="blue", lwd=2)

  x <- rowMeans(replicate(10000, sort(rnorm(n, mean=0, sd=1))))
  plot(density(x), col="red", lwd=2)
}

Answer 1

Вы пытаетесь создать 100 чисел с приблизительным нормальным распределением со средним точно нулем и sd ровно одним? Сделай это:

Начните примерно:

> X = rnorm(100)

Сдвинь их:

> X = X-mean(X)

Масштабировать их:

> X = X/sd(X)

Проверь это:

> mean(X)
[1] -7.223497e-18

достаточно близко

> sd(X)
[1] 1

грохнуть

Это то же самое, что scale функция делает:

> X = rnorm(100)
> mean(X)
[1] -0.007667039
> sd(X)
[1] 0.9336842
> sx = scale(X)
> mean(sx)
[1] 1.437056e-17
> sd(sx)
[1] 1

Answer 2

Если вы хотите детерминистическое решение, это должно работать

qnorm(seq(0.01, 0.99, length.out = 100))

Обратите внимание, что qnorm(0) дает $-\infty$ и qnorm(1) $\infty$, поэтому вам нужно найти разумные границы.

За n=100границы 0,01 и 0,99 работают лучше всего. Если вы хотите, чтобы границы для детерминированного решения находились дальше, вам нужно увеличить n,

Answer 3

Вы можете использовать пакет bayestestR:

library(bayestestR)
x <-  rnorm_perfect(n = 100, mean = 0, sd = 1)
plot(density(x))

Answer 4

Последовательность с низким расхождением? халтон, форе, соболь, хаммерсли: пример:

library(randtoolbox)

sequence <-sobol(n=100, dim = 1, init = TRUE, scrambling = 0, seed = 4711, normal = FALSE)
mean(sequence)
[1] 0.4982031
sd(sequence)
[1] 0.2860574

#trial with prng
set.seed(1) 
sequence2 <- runif(100)
mean(sequence2)
[1] 0.5178471
sd(sequence2)
[1] 0.2675848

с таким же количеством точек последовательность с низким расхождением лучше, чем генератор псевдослучайного числа, имейте в виду, что для равномерной случайной выборки истинное среднее значение равно 0,5, sd равно 0,2886751 (sqrt(1/12)), посмотрите на числа.

(mean(sequence) - 0.5)/0.5   #  -0.0008984375
(mean(sequence2) - 0.5)/0.5  #  -0.008923532
(sd(sequence) - sqrt(1/12))*sqrt(12)
[1] -0.009067992
(sd(sequence2) - sqrt(1/12))*sqrt(12)
[1] -0.07305918

~ В 10 раз лучше, попробуйте с другим семенем, если вы не верите в это

ks.test(sequence,"runif")

    One-sample Kolmogorov-Smirnov test

data:  sequence
D = 0.96268, p-value < 2.2e-16
alternative hypothesis: two-sided

> ks.test(sequence2,"runif")

    One-sample Kolmogorov-Smirnov test

data:  sequence2
D = 0.93956, p-value < 2.2e-16
alternative hypothesis: two-sided

Теперь немного балансировки:

    sequence <- c(sequence, 1.0 - sequence)  #balancing the mean = use antithetics
    #or if you want (sequence <- sequence - mean(sequence))
    normal_sample <- qnorm(sequence)
    normal_sample <- normal_sample/sd(normal_sample)
    plot(normal_sample)