Полигональные градиенты
Я работаю над проектом, который использует библиотеку Juce для отображения графики. До сих пор я использовал API-функции библиотеки для генерации линейных и радиальных градиентов, однако это только два типа градиентов, которые поддерживает эта библиотека. Теперь мне нужно создать градиент другого типа, который повторяет форму правильного выпуклого многоугольника. Ключевое слово здесь - РЕГУЛЯРНОЕ, означающее многоугольник со всеми ребрами одинаковой длины и со всеми вершинами, лежащими на одном круге.
Для случая пятиугольника, вот картинка, чтобы лучше показать результат, который я хотел бы получить: http://www.filterforge.com/wiki/index.php/Polygonal_Gradient
Для моего приложения я хочу иметь возможность указывать многоугольный градиент с любым количеством ребер. (пятиугольник, шестиугольник, восьмиугольник и т. д.)
Учитывая ограничения API, единственный способ получить желаемый результат - заполнить матрицу поверхности пикселем за пикселем, математически рассчитав значения компонентов R, G, B, A для каждого пикселя.
Вот код, который у меня есть:
void render_surface(unsigned char *surface_data,
int width, int height, int linestride,
int num_vertices, t_rgba *color1, t_rgba *color2)
{
const double center_x = 0.5 * width;
const double center_y = 0.5 * height;
const double radius = 0.5 * MIN(width, height);
int x, y;
for (y = height; --y >= 0;) {
uint32_t *line = (uint32_t *)data;
data += linestride;
const double dy = y - center_y;
for (x = width; --x >= 0;) {
const double dx = x - center_x;
double rho = hypot(dx, dy);
rho /= radius; // normalize radius
// constrain
rho = CLIP(rho, 0.0, 1.0);
// interpolate
double a = color2->alpha + (color1->alpha - color2->alpha) * rho;
double r = color2->red + (color1->red - color2->red ) * rho;
double g = color2->green + (color1->green - color2->green) * rho;
double b = color2->blue + (color1->blue - color2->blue ) * rho;
// premultiply alpha
r *= a;
g *= a;
b *= a;
#if LITTLE_ENDIAN
*line++ = ((unsigned int)((256.0 * (1.0 - DBL_EPSILON)) * a) << 24) // alpha
| ((unsigned int)((256.0 * (1.0 - DBL_EPSILON)) * r) << 16) // red
| ((unsigned int)((256.0 * (1.0 - DBL_EPSILON)) * g) << 8) // green
| (unsigned int)((256.0 * (1.0 - DBL_EPSILON)) * b); // blue
#else
*line++ = ((unsigned int)((256.0 * (1.0 - DBL_EPSILON)) * b) << 24) // blue
| ((unsigned int)((256.0 * (1.0 - DBL_EPSILON)) * g) << 16) // green
| ((unsigned int)((256.0 * (1.0 - DBL_EPSILON)) * r) << 8) // red
| (unsigned int)((256.0 * (1.0 - DBL_EPSILON)) * a); // alpha
#endif
}
}
}
Приведенный выше код создает радиальный градиент, тот же тип градиента, который я мог бы создать, используя одну функцию API. Однако, похоже, это хорошая отправная точка для решения проблемы.
surface_data - это матрица из 8-битных значений, представляющих интенсивность пикселей красного, зеленого, синего и альфа-компонентов.
num_vertices - это количество вершин (одинаково расположенных на одном круге), которое мы хотим иметь в нашем полигональном градиенте.
color1 - начальный цвет градиента.
color2 - конечный цвет градиента.
Я хотел бы знать, как я могу заполнить поверхность таким же образом, создавая многоугольный градиент, а не радиальный.
Спасибо за любую помощь.
- Луиджи
Немного переосмыслив эту проблему... если мы рассмотрим начало нашей системы координат как центр многоугольника, то все сводится к тому, чтобы найти уравнение, которое для любой входной точки в декартовых координатах будет равно расстоянию от ближайшего сторона многоугольника.
Моя интуиция подсказывает мне, что должно быть какое-то решение в закрытой форме, потому что:
для круга,
rho = sqrt(dx*dx + dy*dy);
дает нам радиальное расстояние от центра круга, которое можно рассматривать как многоугольник с бесконечными сторонами.
Для квадрата
fmax(fabs(dx), fabs(dy));
дает нам расстояние Чебышева от ближайшей стороны квадрата, которое можно рассматривать как многоугольник с 4 сторонами.
Итак, я думаю, что какая-то комбинация двух формул должна дать промежуточные случаи, которые решат начальную проблему.
Я совершенно не думаю об этом?
- Луиджи
1 ответ
Это примерно, как я бы подошел к этому...
- Поместите центр многоугольника в начале координат "O".
- Для заданной точки "P" в данном сегменте правильного многоугольника, пусть линия через "O" и "P" будет "Line1" и
- пусть линия через внешний край содержащего сегмента многоугольника будет "Line2"
- Найдите точку пересечения 'IP' этих двух линий.
Теперь цветовая доля в P определяется расстоянием P от начала координат относительно расстояния IP до начала координат.
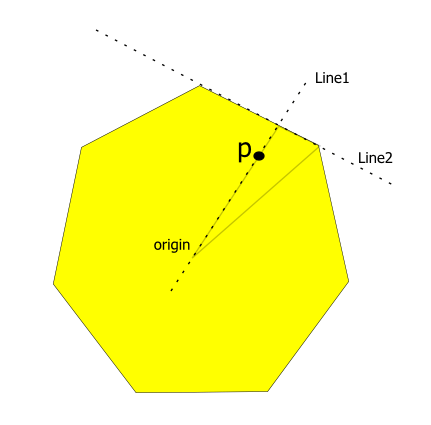
Изменить: я реализовал алгоритм выше, и это вывод...

Edit2: вот код (Delphi)
const
vertical: TFloat = 3.4e38;
function Slope(const pt1, pt2: TFloatPoint): single;
begin
if (pt1.X = pt2.X) then result := vertical
else result := (pt2.Y - pt1.Y)/(pt2.X - pt1.X);
end;
//---------------------------------------------------------------------------
procedure GetLine(const pt1, pt2: TFloatPoint; out m, b: TFloat);
begin
m := Slope(pt1, pt2);
if m = vertical then
b := pt1.X else
b := pt1.Y - m * pt1.X;
end;
//---------------------------------------------------------------------------
function GradientColor(const clr1, clr2: TColor32; fraction: TFloat): TColor32;
begin
if fraction <= 0 then result := clr1
else if fraction >= 1 then result := clr2
else
begin
TColor32Entry(result).B :=
trunc(TColor32Entry(clr2).B * fraction + TColor32Entry(clr1).B * (1-fraction));
TColor32Entry(result).G :=
trunc(TColor32Entry(clr2).G * fraction + TColor32Entry(clr1).G * (1-fraction));
TColor32Entry(result).R :=
trunc(TColor32Entry(clr2).R * fraction + TColor32Entry(clr1).R * (1-fraction));
TColor32Entry(result).A :=
trunc(TColor32Entry(clr2).A * fraction + TColor32Entry(clr1).A * (1-fraction));
end;
end;
//---------------------------------------------------------------------------
function PointInTriangle(const pt, tr1, tr2, tr3: TFloatPoint): boolean;
begin
result := false;
if ((((tr1.Y <= pt.Y) and (pt.Y < tr3.Y)) or
((tr3.Y <= pt.Y) and (pt.Y < tr1.Y))) and
(pt.X < (tr3.X - tr1.X) * (pt.Y - tr1.Y) /
(tr3.Y - tr1.Y) + tr1.X)) then result := not result;
if ((((tr2.Y <= pt.Y) and (pt.Y < tr1.Y)) or
((tr1.Y <= pt.Y) and (pt.Y < tr2.Y))) and
(pt.X < (tr1.X - tr2.X) * (pt.Y - tr2.Y) /
(tr1.Y - tr2.Y) + tr2.X)) then result := not result;
if ((((tr3.Y <= pt.Y) and (pt.Y < tr2.Y)) or
((tr2.Y <= pt.Y) and (pt.Y < tr3.Y))) and
(pt.X < (tr2.X - tr3.X) * (pt.Y - tr3.Y) /
(tr2.Y - tr3.Y) + tr3.X)) then result := not result;
end;
//---------------------------------------------------------------------------
function GetSegmentIndex(vertex: TFloatPoint; vertices: TArrayOfFloatPoint): integer;
var
i, highI: integer;
prev: TFloatPoint;
const
origin: TFloatPoint = (X: 0; Y: 0);
begin
highI := high(vertices);
prev := vertices[highI];
result := -1;
for i := 0 to highI do
begin
if PointInTriangle(vertex, origin, prev, vertices[i]) then
begin
result := i;
break;
end;
prev := vertices[i];
end;
end;
//---------------------------------------------------------------------------
procedure RegularPolygonFill(bmp: TBitmap32; const origin: TPoint;
radius: TFloat; vertexCount: integer; InnerColor, OuterColor: TColor32);
var
i,j,d,q: integer;
dist1,dist2: TFloat;
vert, intersetPt: TFloatPoint;
verts: TArrayOfFloatPoint;
edgeMs, edgeBs: TArrayOfFloat;
angle, angleDiff, m, b: TFloat;
sinAngle, cosAngle: extended;
const
orig: TFloatPoint = (X: 0; Y: 0);
begin
if vertexCount < 3 then exit;
setlength(verts, vertexCount);
setlength(edgeMs, vertexCount); //edge slopes (ie y = M*x +b)
setlength(edgeBs, vertexCount); //edge offsets (ie y = m*x +B)
angleDiff := pi *2 / vertexCount;
angle := angleDiff;
vert.X := radius; //vert used here as prev vertex
vert.Y := 0;
for i := 0 to vertexCount -1 do
begin
SinCos(angle, sinAngle, cosAngle);
verts[i].X := cosAngle * radius;
verts[i].Y := sinAngle * radius;
GetLine(vert, verts[i], edgeMs[i], edgeBs[i]);
angle := angle + angleDiff;
vert := verts[i];
end;
d := floor(radius);
for i := -d to d do
for j := -d to d do
begin
vert := FloatPoint(i,j);
GetLine(orig, vert, m, b);
q := GetSegmentIndex(vert, verts);
if q < 0 then continue;
//simultaneous equations to find intersection ...
//y = m * x + b; y = edgeMs[q]* x + edgeBs[q];
//edgeMs[q]* x + edgeBs[q] = m * x + b;
//(edgeMs[q] - m) * x = b - edgeBs[q]
//x = (b - edgeBs[q])/(edgeMs[q] - m)
if m = vertical then
begin
intersetPt.X := b;
intersetPt.Y := edgeMs[q]* intersetPt.X + edgeBs[q];
end
else if edgeMs[q] = vertical then
begin
intersetPt.X := edgeBs[q];
intersetPt.Y := m* intersetPt.X + b;
end else
begin
intersetPt.X := (b - edgeBs[q])/(edgeMs[q] - m);
intersetPt.Y := m * intersetPt.X + b;
end;
//get distances from origin of vert and intersetPt ...
dist1 := sqrt(vert.X*vert.X + vert.Y*vert.Y);
dist2 := sqrt(intersetPt.X*intersetPt.X + intersetPt.Y*intersetPt.Y);
bmp.Pixel[i + origin.X, j + origin.Y] :=
GradientColor(InnerColor, OuterColor, dist1/dist2);
end;
end;
Моя интуиция подсказывает мне, что должно быть какое-то решение в закрытой форме
Есть...
Аналсис
Для этого я взял формулу расстояния от центра до края шестиугольника (здесь) и заметил, что ее можно обобщить на любой многоугольник. В этой конкретной формуле постояннаяsqrt(3)используется (который я сейчас назову z). Это число эквивалентно удвоенному отношению расстояния между средней точкой многоугольника и средней точкой одного из его ребер по сравнению с расстоянием между средней точкой и одной из его вершин (это расстояние равно 1 в многоугольнике единичной длины).
Итак, эта константа (которая равна sqrt(3) для шестиугольников) определяется как:
Это соотношение, которое я описал ранее, определяется следующим образом:
Обратите внимание, что 2s сокращаются, поэтому общая функция для получения этой константы для любого многоугольника:
SIDES количество сторон многоугольника (например, 6 для шестиугольника)
Теперь мы просто подставляем эту константу в формулу отношения a, где точка лежит на заданном многоугольнике единичной длины по сравнению с тем местом, где она будет лежать на окружности единичной длины:
пример
Как это работает, показано ниже для шестиугольника (таким образом, SIDES=6 и z = sqrt (3)). Мы получаем d как 0,866 для θ=30° и d как 0,897 для θ=45° (также эквивалент θ=15°).
Обратите внимание, что d правильно определен только для 0 <= θ <= segmentAngle (который задается2PI/SIDES в радианах).
Реализация
Теперь у нас есть все, что нужно для кодирования решения.
Следующая функция преобразует 2D координату (пиксель) в число от 0 до 1; это число указывает, в какой точке (шаге) цветового градиента происходит каждый пиксель.
В конечном счете, это очень похоже на радиальный градиент, где евклидово расстояние между пикселем и средней точкой круга используется для определения шага пикселя. Однако с многоугольными градиентами мы хотим масштабировать евклидово расстояние между пикселем (x,y) и средней точкой многоугольника на d, чтобы цвета "сдвигались" к краям многоугольника.
Когда дело доходит до рендеринга, единственное, что нужно умножить d на adenominator чтобы полигон отображался в соответствующем масштабе.
Код
public void polygonGradient(colour[][] pixels, Gradient gradient, Vector2 midPoint, float angle, float zoom, int sides) {
final double z = Math.tan(HALF_PI - (PI / sides)); // z, as derived in answer
final double SEGMENT_ANGLE = (2 * PI) / sides; // max angle of polygon segment in radians
angle %= SEGMENT_ANGLE; // mod angle to minimise difference between theta and SEGMENT_ANGLE in loop (less while calls)
final double denominator = 1 / ((Math.max(pixels.height, pixels.width)) * zoom); // calc here once, not in loop
double yDist; // y distance between midpoint and a given pixel
double xDist; // x distance between midpoint and a given pixel
for (int y = 0, x; y < pixels.height; ++y) {
yDist = (midPoint.y - y) * (midPoint.y - y);
for (x = 0; x < pixels.width; ++x) {
xDist = (midPoint.x - x) * (midPoint.x - x);
double theta = Math.atan2((midPoint.y - y), (midPoint.x - x));
theta += (TWO_PI - angle); // TWO_PI - angle, so we rotate clockwise
theta = Math.abs(theta); // abs() here to simplify while loop
// polygon is split into N segments; restrict theta to angle of one segment
while (theta > SEGMENT_ANGLE) { // effectively modulo (faster than using % operator)
theta -= SEGMENT_ANGLE;
}
final double pointDistance = Math.sqrt(yDist + xDist); // euclidean dist between (x,y) and midpoint
double d = z * (z * Math.cos(theta) + Math.sin(theta)); // d, as derived in answer
// now calculate the position of the pixel on the gradient
double step = d * denominator * pointDistance; // multiply euclidean distance by d
if (step > 1) { // clamp to 1
step = 1;
}
pixels[x][y] = gradient.colourAt(step); // get the colour of the gradient at the step given by dist
}
}
}
Выход
Стороны = 6
Стороны = 9
Стороны = 3; немного увеличено; средняя точка вне центра
