Разбиение списков чисел за полиномиальное время на одинаковые произведения

Question

У меня есть список натуральных чисел L=(n1,n2,...,nk)

Я хочу разделить этот список на 2 списка L1 и L2 так, чтобы произведение элементов в списках было одинаковым.

Таким образом, произведение (L1) списка L1=(l1,...,lx) равно l1*l2*...*lx. Я хочу минимизировать абс (продукт (L1)-продукт (L2)).

Есть ли способ для этого с полиномиальным алгоритмом?

Кроме того, мне было бы интересно получить обобщенную форму, разбив исходный список на k частей, причем все они должны быть как можно более одинаковыми.

Я думаю, что это может быть связано с проблемой подмножества суммы, то есть NP. Спасибо всем заранее.

Answer 1

Чтобы проанализировать это, возьмите журналы продуктов элементов ваших двух подмножеств (log(l1*l2*...*lx) = log(l1)+log(l2)+...+log(lx)). Поскольку вам нужно назначить все свои номера, лучшим назначением подмножества будет просто то, где суммы журналов двух продуктов максимально близки.

Проблема разбиения является частным случаем этой проблемы, и, поскольку эта проблема является NP-полной, ваша проблема также.

Тем не менее, вы все равно сможете решить эту проблему достаточно эффективно, используя целочисленную оптимизацию. Назначить двоичную переменную x_i на каждый номер i; все значения 1 назначены одному набору, а все значения 0 назначены другому. Тогда у вас есть следующая проблема оптимизации:

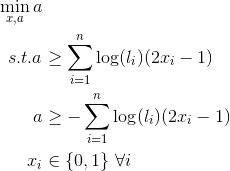
В этой модели 2x_i-1 добавляет log(l_i) значение, если x_i=1 и вычитает, если x_i=0и пара сил ограничений a быть больше или равно абсолютному значению различий в суммированных журналах.

Так как SO - это веб-сайт, ориентированный в первую очередь на проблемы программирования, я добавлю немного кода R, который решает эту проблему оптимизации, используя lpSolve пакет. Существует множество бесплатных и несвободных опций для оптимизации программного обеспечения.

library(lpSolve)
minProd <- function(vals) {
  # Setup and solve optimization problem
  c1 <- c(-2*log(vals), 1)
  rhs1 <- -sum(log(vals))
  c2 <- c(2*log(vals), 1)
  rhs2 <- sum(log(vals))
  obj <- c(rep(0, length(vals)), 1)
  res <- lp("min", obj, rbind(c1, c2), ">=", c(rhs1, rhs2),
            binary.vec=seq(length(vals)))

  # Output solution
  s0 <- vals[res$solution[seq(length(vals))] < 0.001]
  s1 <- vals[res$solution[seq(length(vals))] > 0.999]
  print(paste(paste(s0, collapse="*"), "=", prod(s0)))
  print(paste(paste(s1, collapse="*"), "=", prod(s1)))
}
minProd(c(2, 3, 6))
# [1] "6 = 6"
# [1] "2*3 = 6"
minProd(c(2, 3, 4, 5, 6, 7, 8, 9, 10))
# [1] "4*6*8*10 = 1920"
# [1] "2*3*5*7*9 = 1890"