Найти контрольную точку на кусочно-квадратичной кривой Безье

Question

Мне нужно написать программу для генерации и отображения кусочно-квадратичной кривой Безье, которая интерполирует каждый набор точек данных (у меня есть текстовый файл содержит точки данных). Кривая должна иметь непрерывные направления касательной, причем направление касательной в каждой точке данных является выпуклой комбинацией двух соседних направлений хорды.

0.1 0, 
0 0,
0 5,
0.25 5,
0.25 0, 
5 0, 
5 5, 
10 5,
10 0, 
9.5 0

Выше приведены данные, которые у меня есть, кто-нибудь знает, какую формулу я могу использовать для расчета контрольных точек?

Answer 1

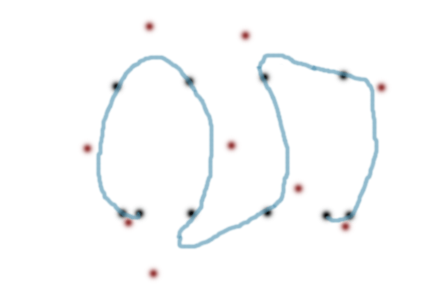
Вам нужно будет использовать кубический Безье, чтобы хорошо обрабатывать множественные изменения наклона, которые происходят в вашем наборе данных. С квадратичными кривыми Безье существует только одна контрольная точка между точками данных, поэтому каждый сегмент кривой должен находиться на одной стороне отрезка соединительной линии.

Сложно объяснить, поэтому вот быстрый набросок ваших данных (черные точки) и квадратичных контрольных точек (красный) и кривой (синий). (Притворись, что кривая плавная!)

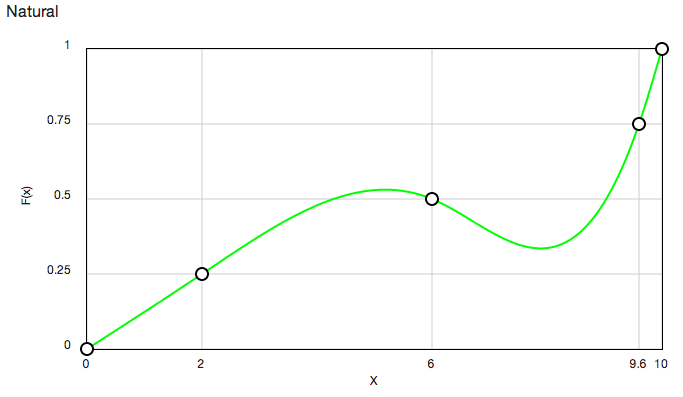
Посмотрите на кривые кубического Эрмита для общего решения.

Answer 2

Отсюда: http://blog.mackerron.com/2011/01/01/javascript-cubic-splines/

Чтобы получить интерполированные кривые, подобные этим:

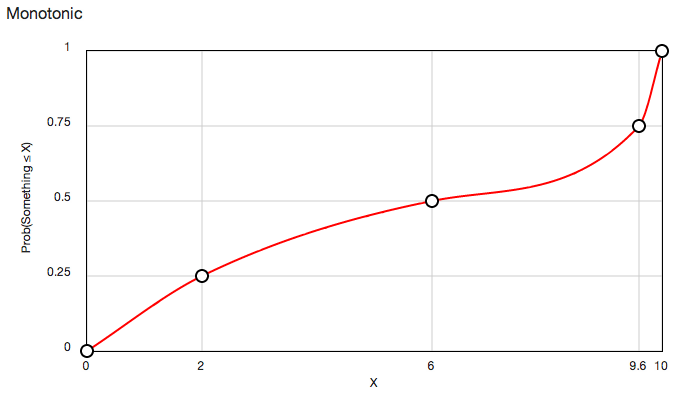
Вы можете использовать этот класс coffee-script (который компилируется в javascript)

class MonotonicCubicSpline

# by George MacKerron, mackerron.com

# adapted from: 
# http://sourceforge.net/mailarchive/forum.php?thread_name=
# EC90C5C6-C982-4F49-8D46-A64F270C5247%40gmail.com&forum_name=matplotlib-users
# (easier to read at http://old.nabble.com/%22Piecewise-Cubic-Hermite-Interpolating-
# Polynomial%22-in-python-td25204843.html)

# with help from:
# F N Fritsch & R E Carlson (1980) 'Monotone Piecewise Cubic Interpolation', 
#   SIAM Journal of Numerical Analysis 17(2), 238 - 246.
# http://en.wikipedia.org/wiki/Monotone_cubic_interpolation
# http://en.wikipedia.org/wiki/Cubic_Hermite_spline

constructor: (x, y) ->
  n = x.length
  delta = []; m = []; alpha = []; beta = []; dist = []; tau = []
  for i in [0...(n - 1)]
    delta[i] = (y[i + 1] - y[i]) / (x[i + 1] - x[i])
    m[i] = (delta[i - 1] + delta[i]) / 2 if i > 0
  m[0] = delta[0]
  m[n - 1] = delta[n - 2]
  to_fix = []
  for i in [0...(n - 1)]
    to_fix.push(i) if delta[i] == 0
  for i in to_fix
    m[i] = m[i + 1] = 0
  for i in [0...(n - 1)]
    alpha[i] = m[i] / delta[i]
    beta[i]  = m[i + 1] / delta[i] 
    dist[i]  = Math.pow(alpha[i], 2) + Math.pow(beta[i], 2)
    tau[i]   = 3 / Math.sqrt(dist[i])
  to_fix = []
  for i in [0...(n - 1)]
    to_fix.push(i) if dist[i] > 9
  for i in to_fix
    m[i]     = tau[i] * alpha[i] * delta[i]
    m[i + 1] = tau[i] * beta[i]  * delta[i]
  @x = x[0...n]  # copy
  @y = y[0...n]  # copy
  @m = m

interpolate: (x) ->
  for i in [(@x.length - 2)..0]
    break if @x[i] <= x
  h = @x[i + 1] - @x[i]
  t = (x - @x[i]) / h
  t2 = Math.pow(t, 2)
  t3 = Math.pow(t, 3)
  h00 =  2 * t3 - 3 * t2 + 1
  h10 =      t3 - 2 * t2 + t
  h01 = -2 * t3 + 3 * t2
  h11 =      t3  -    t2
  y = h00 * @y[i] + 
      h10 * h * @m[i] + 
      h01 * @y[i + 1] + 
      h11 * h * @m[i + 1]
  y