Как вы проверяете пересечение отрезка и луча, исходящего из точки под углом от горизонтали?
Для данного отрезка прямой это две точки (x1,y1) и (x2,y2), одна точка P(x,y) и угол тета. Как мы узнаем, пересекается ли этот отрезок и луч, исходящий от P под углом тета от горизонтали, или нет? Если они пересекаются, как найти точку пересечения?
5 ответов
Давайте обозначим точки q = (x1, y1) и q + s = (x2, y2). Следовательно, s = (x2 - x1, y2 - y1). Тогда проблема выглядит так:
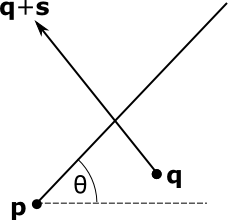
Пусть r = (cosθ, sinθ). Тогда любая точка на луче через p представляется как p + t r (для скалярного параметра 0 ≤ t), а любая точка на отрезке прямой представляется как q + u s (для скалярного параметра 0 ≤ u ≤ 1).
Две линии пересекаются, если мы можем найти t и u такие, что p + t r = q + u s:

Посмотрите этот ответ, чтобы узнать, как найти эту точку (или определить, что такой точки нет).
Тогда ваш отрезок пересекает луч, если 0 ≤ t и 0 ≤ u ≤ 1.
Вот код C# для алгоритма, приведенный в других ответах:
/// <summary>
/// Returns intersection point on ray or null if there is no intersection.
/// </summary>
public double? GetRayToLineSegmentIntersection(Point rayOrigin, Vector rayDirection, Point point1, Point point2)
{
var v1 = rayOrigin - point1;
var v2 = point2 - point1;
var v3 = new Vector(-rayDirection.Y, rayDirection.X);
var dot = v2 * v3;
if (Math.Abs(dot) < 0.000001)
return null;
var t1 = Vector.CrossProduct(v2, v1) / dot;
var t2 = (v1 * v3) / dot;
if (t1 >= 0.0 && (t2 >= 0.0 && t2 <= 1.0))
return t1;
return null;
}
Спасибо Гарету за отличный ответ. Вот решение, реализованное в Python. Не стесняйтесь удалять тесты и просто скопируйте и вставьте актуальную функцию. Я следовал за описанием методов, которые появились здесь, https://rootllama.wordpress.com/2014/06/20/ray-line-segment-intersection-test-in-2d/.
import numpy as np
def magnitude(vector):
return np.sqrt(np.dot(np.array(vector),np.array(vector)))
def norm(vector):
return np.array(vector)/magnitude(np.array(vector))
def lineRayIntersectionPoint(rayOrigin, rayDirection, point1, point2):
"""
>>> # Line segment
>>> z1 = (0,0)
>>> z2 = (10, 10)
>>>
>>> # Test ray 1 -- intersecting ray
>>> r = (0, 5)
>>> d = norm((1,0))
>>> len(lineRayIntersectionPoint(r,d,z1,z2)) == 1
True
>>> # Test ray 2 -- intersecting ray
>>> r = (5, 0)
>>> d = norm((0,1))
>>> len(lineRayIntersectionPoint(r,d,z1,z2)) == 1
True
>>> # Test ray 3 -- intersecting perpendicular ray
>>> r0 = (0,10)
>>> r1 = (10,0)
>>> d = norm(np.array(r1)-np.array(r0))
>>> len(lineRayIntersectionPoint(r0,d,z1,z2)) == 1
True
>>> # Test ray 4 -- intersecting perpendicular ray
>>> r0 = (0, 10)
>>> r1 = (10, 0)
>>> d = norm(np.array(r0)-np.array(r1))
>>> len(lineRayIntersectionPoint(r1,d,z1,z2)) == 1
True
>>> # Test ray 5 -- non intersecting anti-parallel ray
>>> r = (-2, 0)
>>> d = norm(np.array(z1)-np.array(z2))
>>> len(lineRayIntersectionPoint(r,d,z1,z2)) == 0
True
>>> # Test ray 6 --intersecting perpendicular ray
>>> r = (-2, 0)
>>> d = norm(np.array(z1)-np.array(z2))
>>> len(lineRayIntersectionPoint(r,d,z1,z2)) == 0
True
"""
# Convert to numpy arrays
rayOrigin = np.array(rayOrigin, dtype=np.float)
rayDirection = np.array(norm(rayDirection), dtype=np.float)
point1 = np.array(point1, dtype=np.float)
point2 = np.array(point2, dtype=np.float)
# Ray-Line Segment Intersection Test in 2D
# http://bit.ly/1CoxdrG
v1 = rayOrigin - point1
v2 = point2 - point1
v3 = np.array([-rayDirection[1], rayDirection[0]])
t1 = np.cross(v2, v1) / np.dot(v2, v3)
t2 = np.dot(v1, v3) / np.dot(v2, v3)
if t1 >= 0.0 and t2 >= 0.0 and t2 <= 1.0:
return [rayOrigin + t1 * rayDirection]
return []
if __name__ == "__main__":
import doctest
doctest.testmod()
Примечание: это решение работает без создания векторных классов или определения векторного умножения/деления, но его реализация требует больше времени. Это также позволяет избежать ошибок деления на ноль. Если вам просто нужен блок кода и вас не волнует вывод, прокрутите сообщение до конца.
Допустим, у нас есть луч, определяемый x, y и тета, и линия, определяемая x1, y1, x2 и y2.
Во-первых, давайте нарисуем два луча, которые указывают от начала луча до концов отрезка. В псевдокоде это
theta1 = atan2(y1-y, x1-x);
theta2 = atan2(y2-y, x2-x);
Далее мы проверяем, находится ли луч внутри этих двух новых лучей. Все они имеют одинаковое происхождение, поэтому нам нужно проверить только углы.
Чтобы сделать это проще, давайте сдвинем все углы так, чтобы тета1 находилась на оси x, а затем вернём всё обратно в диапазон от -пи до пи. В псевдокоде это
dtheta = theta2-theta1; //this is where theta2 ends up after shifting
ntheta = theta-theta1; //this is where the ray ends up after shifting
dtheta = atan2(sin(dtheta), cos(dtheta))
ntheta = atan2(sin(ntheta), cos(ntheta))
(Примечание: взятие atan2 для sin и cos угла просто сбрасывает диапазон угла в пределах -pi и pi без изменения угла.)
Теперь представьте, что вы рисуете линию от нового местоположения тета2 (dtheta) до нового местоположения тета1 (0 радиан). Вот где сегмент линии закончился.
Единственный момент, когда луч пересекает линейный сегмент, это когда тета находится между тета1 и тета2, что совпадает с тем, когда nтета находится между dтета и 0 радиан. Вот соответствующий псевдокод:
sign(ntheta)==sign(dtheta)&&
abs(ntheta)<=abs(dtheta)
Это скажет вам, пересекаются ли две линии. Вот он в одном блоке псевдокода:
theta1=atan2(y1-y, x1-x);
theta2=atan2(y2-y, x2-x);
dtheta=theta2-theta1;
ntheta=theta-theta1;
dtheta=atan2(sin(dtheta), cos(dtheta))
ntheta=atan2(sin(ntheta), cos(ntheta))
return (sign(ntheta)==sign(dtheta)&&
abs(ntheta)<=abs(dtheta));
Теперь, когда мы знаем, что точки пересекаются, нам нужно найти точку пересечения. Здесь мы будем работать с совершенно чистого листа, поэтому мы можем игнорировать любой код вплоть до этой части. Чтобы найти точку пересечения, вы можете использовать следующую систему уравнений и решить для xp и yp, где lb и rb — точки пересечения y отрезка и луча соответственно.
y1=(y2-y1)/(x2-x1)*x1+lb
yp=(y2-y1)/(x2-x1)*xp+lb
y=sin(theta)/cos(theta)*x+rb
yp=sin(theta)/cos(theta)*x+rb
Это дает следующие формулы для xp и yp:
xp=(y1-(y2-y1)/(x2-x1)*x1-y+sin(theta)/cos(theta)*x)/(sin(theta)/cos(theta)-(y2-y1)/(x2-x1));
yp=sin(theta)/cos(theta)*xp+y-sin(theta)/cos(theta)*x
Который можно сократить, используя lm=(y2-y1)/(x2-x1) и rm=sin(theta)/cos(theta)
xp=(y1-lm*x1-y+rm*x)/(rm-lm);
yp=rm*xp+y-rm*x;
Вы можете избежать ошибок деления на ноль, проверяя, является ли линия или луч вертикальным, а затем заменяя каждый x и y друг другом. Вот соответствующий псевдокод:
if(x2-x1==0||cos(theta)==0){
let rm=cos(theta)/sin(theta);
let lm=(x2-x1)/(y2-y1);
yp=(x1-lm*y1-x+rm*y)/(rm-lm);
xp=rm*yp+x-rm*y;
}else{
let rm=sin(theta)/cos(theta);
let lm=(y2-y1)/(x2-x1);
xp=(y1-lm*x1-y+rm*x)/(rm-lm);
yp=rm*xp+y-rm*x;
}
TL;DR:
bool intersects(x1, y1, x2, y2, x, y, theta){
theta1=atan2(y1-y, x1-x);
theta2=atan2(y2-y, x2-x);
dtheta=theta2-theta1;
ntheta=theta-theta1;
dtheta=atan2(sin(dtheta), cos(dtheta))
ntheta=atan2(sin(ntheta), cos(ntheta))
return (sign(ntheta)==sign(dtheta)&&abs(ntheta)<=abs(dtheta));
}
point intersection(x1, y1, x2, y2, x, y, theta){
let xp, yp;
if(x2-x1==0||cos(theta)==0){
let rm=cos(theta)/sin(theta);
let lm=(x2-x1)/(y2-y1);
yp=(x1-lm*y1-x+rm*y)/(rm-lm);
xp=rm*yp+x-rm*y;
}else{
let rm=sin(theta)/cos(theta);
let lm=(y2-y1)/(x2-x1);
xp=(y1-lm*x1-y+rm*x)/(rm-lm);
yp=rm*xp+y-rm*x;
}
return (xp, yp);
}
См. Этот ответ для получения полностью векторизованной реализации Python для обработки нескольких лучей и нескольких сегментов на основе ответа Гарета .