mgcv: как извлечь узлы, базис, коэффициенты и прогнозы для P-сплайнов в адаптивном сглаживании?

Question

Я использую пакет mgcv в R, чтобы подогнать некоторые полиномиальные сплайны к некоторым данным через:

x.gam <- gam(cts ~ s(time, bs = "ad"), data = x.dd,
             family = poisson(link = "log"))

Я пытаюсь извлечь функциональную форму подгонки. x.gam это gamObjectи я читал документацию, но не нашел достаточно информации для того, чтобы вручную восстановить подобранную функцию.

• x.gam$smooth содержит информацию о том, были ли размещены узлы;
• x.gam$coefficients дает коэффициенты сплайна, но я не знаю, в каком порядке используются полиномиальные сплайны, и поиск в коде ничего не выявил.

Есть ли аккуратный способ извлечения используемых узлов, коэффициентов и базиса, чтобы можно было вручную восстановить подгонку?

Answer 1

У меня нет ваших данных, поэтому я беру следующий пример из ?adaptive.smooth чтобы показать вам, где вы можете найти информацию, которую вы хотите. Обратите внимание, что хотя этот пример предназначен для данных Гаусса, а не для данных Пуассона, отличается только функция связи; все остальные просто стандартные.

 x <- 1:1000/1000  # data between [0, 1]
 mu <- exp(-400*(x-.6)^2)+5*exp(-500*(x-.75)^2)/3+2*exp(-500*(x-.9)^2)
 y <- mu+0.5*rnorm(1000)
 b <- gam(y~s(x,bs="ad",k=40,m=5))

Теперь вся информация о плавном построении хранится в b$smoothвынимаем это:

smooth <- b$smooth[[1]]  ## extract smooth object for first smooth term

узлы:

smooth$knots дает вам местоположение узлов.

> smooth$knots
 [1] -0.081161 -0.054107 -0.027053  0.000001  0.027055  0.054109  0.081163
 [8]  0.108217  0.135271  0.162325  0.189379  0.216433  0.243487  0.270541
[15]  0.297595  0.324649  0.351703  0.378757  0.405811  0.432865  0.459919
[22]  0.486973  0.514027  0.541081  0.568135  0.595189  0.622243  0.649297
[29]  0.676351  0.703405  0.730459  0.757513  0.784567  0.811621  0.838675
[36]  0.865729  0.892783  0.919837  0.946891  0.973945  1.000999  1.028053
[43]  1.055107  1.082161

Обратите внимание, три внешних узла расположены за каждой стороной [0, 1] построить сплайн-основу.

базовый класс

attr(smooth, "class") говорит вам тип сплайна. Как вы можете прочитать из ?adaptive.smooth, за bs = ad, mgcv используйте P-сплайны, поэтому вы получите "pspline.smooth".

mgcv используйте pspline 2-го порядка, вы можете проверить это, проверив матрицу разностей smooth$D, Ниже приведен снимок:

> smooth$D[1:6,1:6]
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    1   -2    1    0    0    0
[2,]    0    1   -2    1    0    0
[3,]    0    0    1   -2    1    0
[4,]    0    0    0    1   -2    1
[5,]    0    0    0    0    1   -2
[6,]    0    0    0    0    0    1

коэффициенты

Вы уже знали, что b$coefficients содержать коэффициенты модели:

beta <- b$coefficients

Обратите внимание, что это именованный вектор:

> beta
(Intercept)      s(x).1      s(x).2      s(x).3      s(x).4      s(x).5 
 0.37792619 -0.33500685 -0.30943814 -0.30908847 -0.31141148 -0.31373448 
     s(x).6      s(x).7      s(x).8      s(x).9     s(x).10     s(x).11 
-0.31605749 -0.31838050 -0.32070350 -0.32302651 -0.32534952 -0.32767252 
    s(x).12     s(x).13     s(x).14     s(x).15     s(x).16     s(x).17 
-0.32999553 -0.33231853 -0.33464154 -0.33696455 -0.33928755 -0.34161055 
    s(x).18     s(x).19     s(x).20     s(x).21     s(x).22     s(x).23 
-0.34393354 -0.34625650 -0.34857906 -0.05057041  0.48319491  0.77251118 
    s(x).24     s(x).25     s(x).26     s(x).27     s(x).28     s(x).29 
 0.49825345  0.09540020 -0.18950763  0.16117012  1.10141701  1.31089436 
    s(x).30     s(x).31     s(x).32     s(x).33     s(x).34     s(x).35 
 0.62742937 -0.23435309 -0.19127140  0.79615752  1.85600016  1.55794576 
    s(x).36     s(x).37     s(x).38     s(x).39 
 0.40890236 -0.20731309 -0.47246357 -0.44855437

матрица базиса / матрица модели / матрица линейного предиктора (lpmatrix)

Вы можете получить матрицу модели из:

mat <- predict.gam(b, type = "lpmatrix")

Это n-by-p матрица, где n количество наблюдений, и p это число коэффициентов. Эта матрица имеет имя столбца:

> head(mat[,1:5])
  (Intercept)    s(x).1    s(x).2      s(x).3      s(x).4
1           1 0.6465774 0.1490613 -0.03843899 -0.03844738
2           1 0.6437580 0.1715691 -0.03612433 -0.03619157
3           1 0.6384074 0.1949416 -0.03391686 -0.03414389
4           1 0.6306815 0.2190356 -0.03175713 -0.03229541
5           1 0.6207361 0.2437083 -0.02958570 -0.03063719
6           1 0.6087272 0.2688168 -0.02734314 -0.02916029

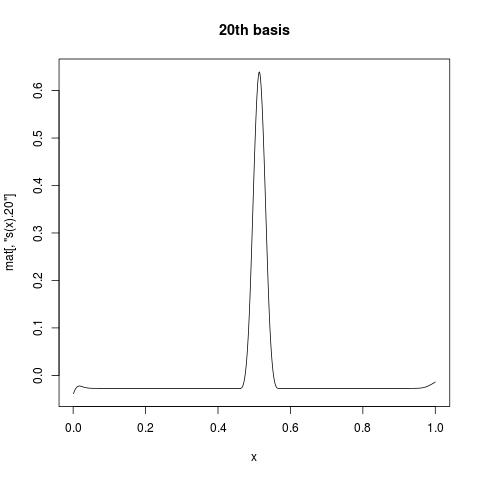
Первый столбец - все 1, дающий перехват. В то время как s(x).1 предлагает первую базисную функцию для s(x), Если вы хотите посмотреть, как выглядит отдельная базовая функция, вы можете построить столбец mat против вашей переменной. Например:

plot(x, mat[, "s(x).20"], type = "l", main = "20th basis")

линейный предиктор

Если вы хотите вручную построить подгонку, вы можете сделать:

pred.linear <- mat %*% beta

Обратите внимание, что это именно то, что вы можете получить от b$linear.predictors или же

predict.gam(b, type = "link")

ответ / установленные значения

Для негауссовых данных, если вы хотите получить переменную ответа, вы можете применить функцию обратной связи к линейному предиктору, чтобы отобразить обратно в исходный масштаб.

Семейная информация хранится в gamObject$family, а также gamObject$family$linkinv является функцией обратной ссылки. Приведенный выше пример наверняка даст вам идентификационную ссылку, но для вашего подобранного объекта x.gam, ты можешь сделать:

x.gam$family$linkinv(x.gam$linear.predictors)

Обратите внимание, это то же самое x.gam$fitted, или же

predict.gam(x.gam, type = "response").

---

Другие ссылки

Я только что понял, что раньше было много подобных вопросов.

1. Этот ответ Гэвина Симпсона великолепен для predict.gam( , type = 'lpmatrix'),
2. Этот ответ о predict.gam(, type = 'terms'),

Но в любом случае, лучшая ссылка всегда ?predict.gam, который включает в себя обширные примеры.