Как восстановить положение пространства вида с учетом значения глубины пространства просмотра и ndc xy
Я пишу отложенный шейдер и пытаюсь упаковать свой gbuffer более плотно. Тем не менее, я не могу рассчитать положение взгляда, учитывая глубину пространства просмотра правильно
// depth -> (gl_ModelViewMatrix * vec4(pos.xyz, 1)).z; where pos is the model space position
// fov -> field of view in radians (0.62831855, 0.47123888)
// p -> ndc position, x, y [-1, 1]
vec3 getPosition(float depth, vec2 fov, vec2 p)
{
vec3 pos;
pos.x = -depth * tan( HALF_PI - fov.x/2.0 ) * (p.x);
pos.y = -depth * tan( HALF_PI - fov.y/2.0 ) * (p.y);
pos.z = depth;
return pos;
}
Вычисленная позиция неверна. Я знаю это, потому что я все еще сохраняю правильную позицию в gbuffer и тестирую, используя это.
3 ответа
3 решения для восстановления положения пространства обзора в перспективной проекции
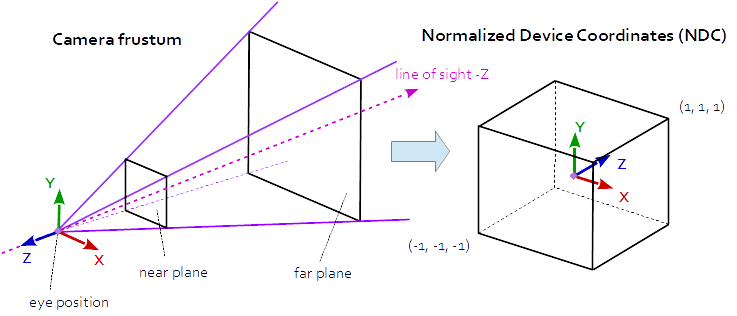
Матрица проекции описывает отображение от трехмерных точек сцены к двухмерным точкам области просмотра. Он преобразуется из пространства вида (глаза) в пространство клипа, а координаты в пространстве клипа преобразуются в нормализованные координаты устройства (NDC) путем деления на компонент w координат клипа. НДЦ находятся в диапазоне (-1,-1,-1) - (1,1,1).
В перспективной проекции матрица проекции описывает отображение из трехмерных точек в мире, как они видны с камеры-обскуры, в двумерные точки видового экрана.
Координаты пространства глаза в усеченной области камеры (усеченная пирамида) отображаются в куб (нормализованные координаты устройства).
Матрица перспективной проекции:
r = right, l = left, b = bottom, t = top, n = near, f = far
2*n/(r-l) 0 0 0
0 2*n/(t-b) 0 0
(r+l)/(r-l) (t+b)/(t-b) -(f+n)/(f-n) -1
0 0 -2*f*n/(f-n) 0
следует:
aspect = w / h
tanFov = tan( fov_y * 0.5 );
prjMat[0][0] = 2*n/(r-l) = 1.0 / (tanFov * aspect)
prjMat[1][1] = 2*n/(t-b) = 1.0 / tanFov
В перспективной проекции Z-компонент вычисляется рациональной функцией:
z_ndc = ( -z_eye * (f+n)/(f-n) - 2*f*n/(f-n) ) / -z_eye
Глубина (gl_FragCoord.z а также gl_FragDepth) рассчитывается следующим образом:
z_ndc = clip_space_pos.z / clip_space_pos.w;
depth = (((farZ-nearZ) * z_ndc) + nearZ + farZ) / 2.0;
1. Поле зрения и соотношение сторон
Поскольку матрица проекции определяется полем зрения и соотношением сторон, можно восстановить положение области просмотра с полем зрения и соотношением сторон. При условии, что это симметричная перспективная проекция и нормализованные координаты устройства, глубина и ближняя и дальняя плоскости известны.
Восстановить расстояние Z в поле зрения:
z_ndc = 2.0 * depth - 1.0;
z_eye = 2.0 * n * f / (f + n - z_ndc * (f - n));
Восстановить положение области просмотра по нормализованным координатам устройства XY:
ndc_x, ndc_y = xy normalized device coordinates in range from (-1, -1) to (1, 1):
viewPos.x = z_eye * ndc_x * aspect * tanFov;
viewPos.y = z_eye * ndc_y * tanFov;
viewPos.z = -z_eye;
2. Проекционная матрица
Параметры проекции, определяемые полем зрения и соотношением сторон, сохраняются в матрице проекции. Поэтому положение окна просмотра можно восстановить по значениям из матрицы проекции из симметричной проекции перспективы.
Обратите внимание на соотношение между матрицей проекции, полем зрения и соотношением сторон:
prjMat[0][0] = 2*n/(r-l) = 1.0 / (tanFov * aspect);
prjMat[1][1] = 2*n/(t-b) = 1.0 / tanFov;
prjMat[2][2] = -(f+n)/(f-n)
prjMat[3][2] = -2*f*n/(f-n)
Восстановить расстояние Z в поле зрения:
A = prj_mat[2][2];
B = prj_mat[3][2];
z_ndc = 2.0 * depth - 1.0;
z_eye = B / (A + z_ndc);
Восстановить положение области просмотра по нормализованным координатам устройства XY:
viewPos.x = z_eye * ndc_x / prjMat[0][0];
viewPos.y = z_eye * ndc_y / prjMat[1][1];
viewPos.z = -z_eye;
3. Матрица обратной проекции
Конечно, положение окна просмотра может быть восстановлено с помощью матрицы обратной проекции.
mat4 inversePrjMat = inverse( prjMat );
vec4 viewPosH = inversePrjMat * vec3( ndc_x, ndc_y, 2.0 * depth - 1.0, 1.0 )
vec3 viewPos = viewPos.xyz / viewPos.w;
Смотрите также ответы на следующий вопрос:
В конце концов мне удалось заставить его работать, так как он отличается от описанного выше метода, я подробно опишу его, чтобы у любого, кто его увидит, было решение.
- Пропуск 1: Сохранение значения глубины в пространстве вида для gbuffer
- Чтобы воссоздать позицию (x, y, z) во втором проходе:
- Передайте горизонтальное и вертикальное поле зрения в радианах в шейдер.
- Передайте расстояние ближней плоскости (ближнее) до шейдера. (расстояние от положения камеры до ближней плоскости)
- Представьте луч от камеры в положение фрагмента. Этот луч пересекает ближнюю плоскость в определенной позиции P. Мы имеем эту позицию в пространстве ndc и хотим вычислить эту позицию в пространстве обзора.
Теперь у нас есть все значения, которые нам нужны в пространстве просмотра. Мы можем использовать закон подобных треугольников, чтобы найти фактическую позицию фрагмента P'
P = P_ndc * near * tan(fov/2.0f) // computation is the same for x, y // Note that by law of similar triangles, P'.x / depth = P/near P'.xy = P/near * -depth; // -depth because in opengl the camera is staring down the -z axis P'.z = depth;
Я написал отложенный шейдер и использовал этот код для пересчета расположения экрана:
vec3 getFragmentPosition()
{
vec4 sPos = vec4(gl_TexCoord[0].x, gl_TexCoord[0].y, texture2D(depthTex, gl_TexCoord[0].xy).x, 1.0);
sPos.z = 2.0 * sPos.z - 1.0;
sPos = invPersp * sPos;
return sPos.xyz / sPos.w;
}
где depthTex это текстура, содержащая информацию о глубине, и invPersp предварительно рассчитанная матрица обратной перспективы Вы берете положение фрагмента экрана и умножаете его на матрицу обратной перспективы, чтобы получить координаты вида модели. Затем вы делите на w чтобы получить однородные координаты. Умножение на два и вычитание на единицу - масштабирование глубины от [0, 1] (как оно хранится в текстуре) до [-1, 1].
Кроме того, в зависимости от того, какой тип MRT вы используете, пересчитанный результат не будет точно равен сохраненной информации, поскольку вы теряете точность с плавающей точкой.