Почему градиентный спуск с импульсом является экспоненциально взвешенным средним?
Недавно я смотрел видео Эндрю Нг на SGDM. Я понимаю, что слагаемое импульса обновляет градиент, взвешивая последний градиент и используя небольшой компонент V_dw. Я не понимаю, почему импульс также известен как экспоненциально взвешенное среднее. Кроме того, в видео Ng в 6:37 он говорит, что использование Beta = 0,9 эффективно означает использование среднего из последних 10 градиентов. Может кто-нибудь объяснить, как это работает? Для меня это всего лишь скалярное взвешивание 1-0,9 для всех градиентов в векторе dW.
Цени любое понимание! Я чувствую, что упускаю что-то фундаментальное. 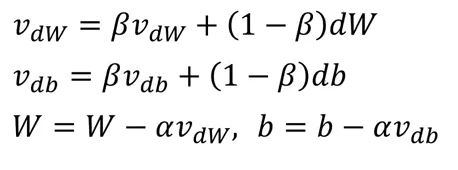
1 ответ
Вам просто нужно подумать о том, что находится в вашем последнем градиенте. Последний градиент уже является взвешенным градиентом из-за члена импульса.
На первом этапе вы просто сделаете градиентный спуск. На втором шаге вы получите градиент импульса m_grad_2 = grad_2 + 0,9 m_grad_1. На третьем шаге у вас снова будет градиент импульса m_grad_3 = grad_3 + 0,9 m_grad_2, но старый градиент состоит из члена импульса. Следовательно, 0,9*m_grad_2 = 0,9 * (град_2 + 0,9 град_1), что составляет 0,9 град_2 + 0,81 град_1. Следовательно, влияние градиента на k-й шаг будет 0,9^k. После 10 шагов воздействие будет совсем небольшим.