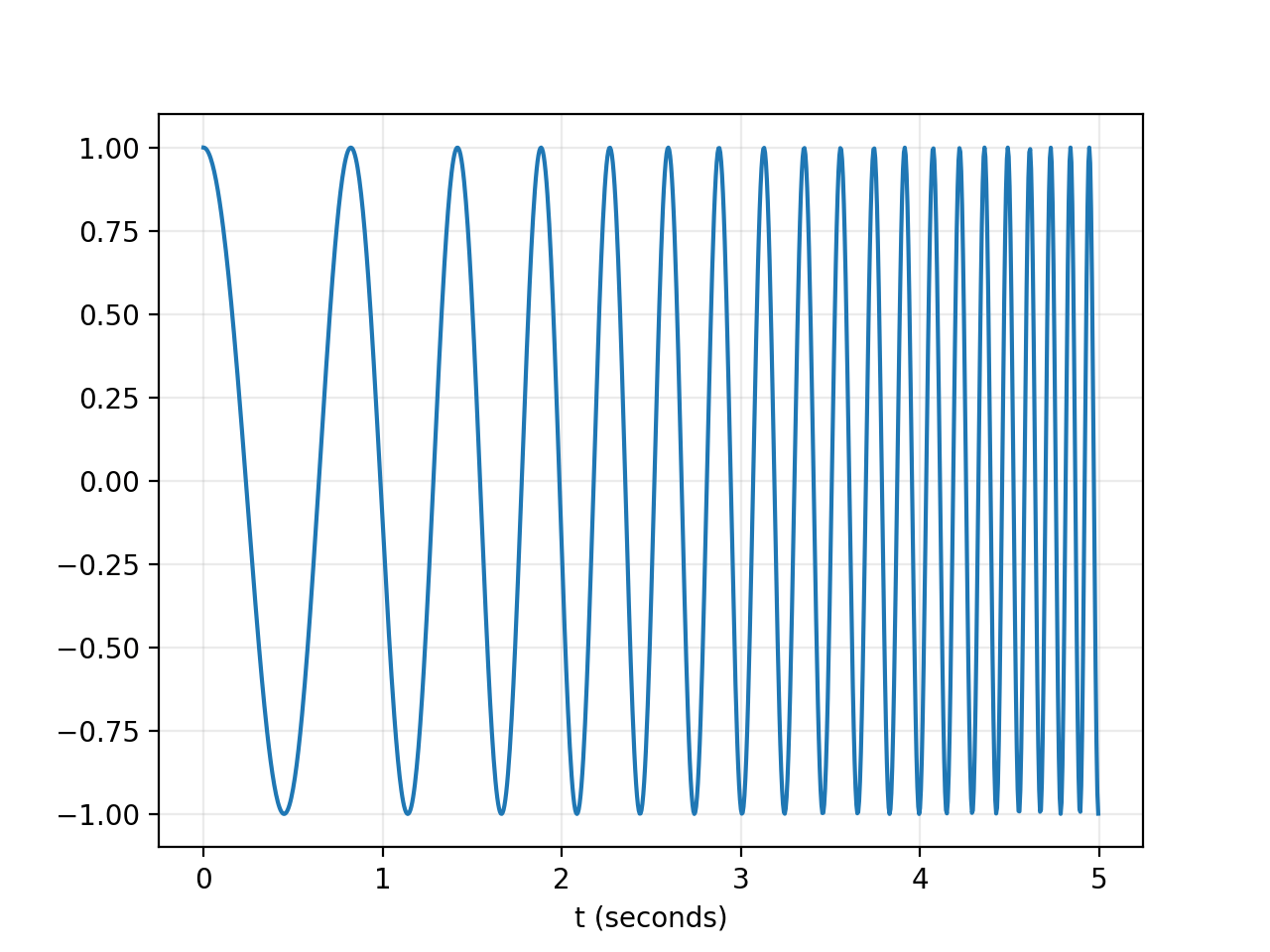
Синусоида, экспоненциально изменяющаяся между частотами f1 и f2 в данное время / количество выборок

Question

Я пытаюсь реализовать метод Python, который генерирует синусоидальную волну, которая экспоненциально возрастает между двумя частотами. Линейное изменение было решено в [этом вопросе] с помощью следующего кода Python:

from math import pi, sin

def sweep(f_start, f_end, interval, n_steps):    
    for i in range(n_steps):
        delta = i / float(n_steps)
        t = interval * delta
        phase = 2 * pi * t * (f_start + (f_end - f_start) * delta / 2)
        print t, phase * 180 / pi, 3 * sin(phase)

sweep(1, 10, 5, 1000)

Как изменить этот линейный накопительный фазовый / дельта-подход, чтобы развернуть экспоненциальную частоту и быть гладким для человеческого слуха.

Answer 1

Ответ Баса великолепен, но на самом деле не дает аналитического решения, так что вот эта часть...

Насколько я могу сказать, вы хотите что-то вроде sin(Aexp(Bt)) где A а также B являются постоянными. Я предполагаю, что время начинается в 0 и продолжает C (если это начинается в другое время, вычтите это из обоих).

Тогда, как сказал Бас, я думаю, если мы sin(g(t)) частота f таков, что 2 * pi * f = dg / dt, И мы хотим, чтобы это было f0 вовремя 0 а также fC вовремя C,

Если вы пройдете математику, что легко (это действительно так - последний год обучения в школе), вы получите:

B = 1/C * log(fC/f0)
A = 2 * pi * f0 / B

и вот код, который идет от 1 до 10 Гц за 5 секунд, используя 1000 выборок:

from math import pi, sin, log, exp

def sweep(f_start, f_end, interval, n_steps):
    b = log(f_end/f_start) / interval
    a = 2 * pi * f_start / b
    for i in range(n_steps):
        delta = i / float(n_steps)
        t = interval * delta
        g_t = a * exp(b * t)
        print t, 3 * sin(g_t)

sweep(1, 10, 5, 1000)

который дает:

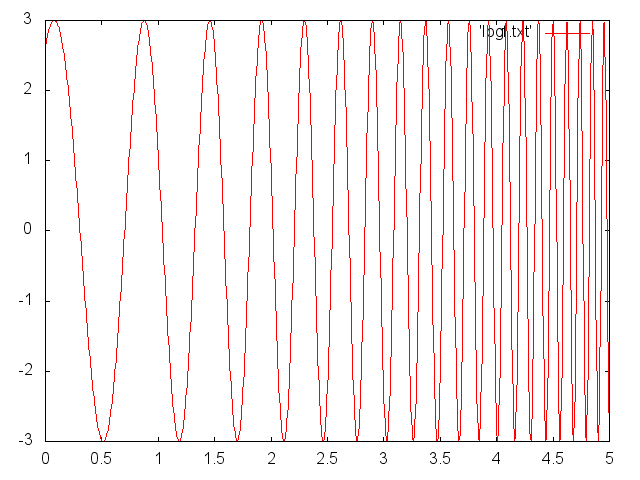
(и вы можете добавить в константу - sin(g_t + k) - чтобы получить начальный этап, где вы хотите).

Обновить

Чтобы показать, что проблема, которую вы видите, является артефактом выборки, вот версия, которая выполняет передискретизацию (если вы установите ее в качестве аргумента):

from math import pi, sin, log, exp

def sweep(f_start, f_end, interval, n_steps, n_oversample=1):
    b = log(f_end/f_start) / interval
    a = 2 * pi * f_start / b
    for i in range(n_steps):
        for oversample in range(n_oversample):
            fractional_step = oversample / float(n_oversample)
            delta = (i + fractional_step) / float(n_steps)
            t = interval * delta
            g_t = a * exp(b * t)
            print t, 3 * sin(g_t)

sweep(16000.0, 16500.0, 256.0/48000.0, 256)      # looks strange
sweep(16000.0, 16500.0, 256.0/48000.0, 256, 4)   # looks fine with better resolution

Если вы проверите код, вы увидите, что все эти настройки n_oversample до 4 (второй вызов) - добавить более высокое разрешение к временным шагам. В частности, код при oversample = 0 (т.е. fractional_step = 0) идентичен предыдущему, поэтому второй график включает точки на первом графике, а также дополнительные, которые "заполняют" недостающие данные и заставляют все выглядеть гораздо менее удивительным.

Вот крупный план оригинала и кривая передискретизации около начала, показывающая, что происходит в деталях:

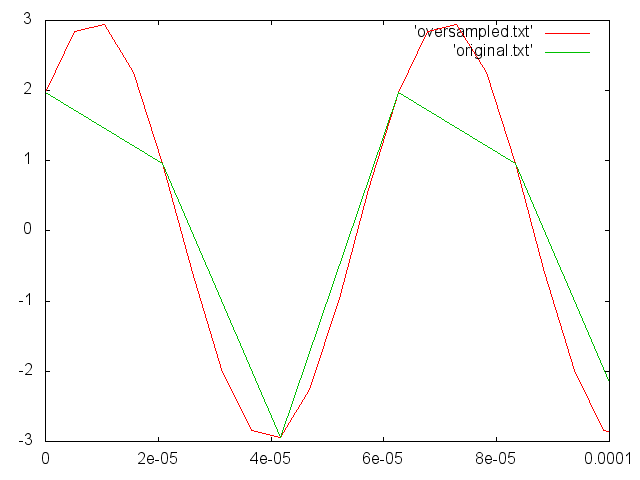
Наконец, подобные вещи совершенно нормальны и не указывают на какую-либо ошибку. Когда аналоговый сигнал генерируется из цифрового сигнала, вы получите "правильный" результат (при условии, что аппаратное обеспечение работает правильно). Это отличное видео объяснит вещи, если они не ясны.

Answer 2

Хитрость в подобных проблемах состоит в том, чтобы понять связь между частотной модуляцией и фазовой модуляцией, эти два тесно связаны. Синус с постоянной частотой f и амплитуда A можно описать как (формулы, а не код Python):

x(t) = A sin(2 * pi * f * t)

но другой способ написать это, сначала определив фазу phi как функция времени:

phi(t) = 2 * pi * f * t
x(t) = A sin(phi(t))

Здесь следует отметить, что частота f является производной фазы, деленной на 2* пи: f = d/dt(phi(t)) / (2*pi),

Для сигнала, частота которого изменяется во времени, вы можете аналогичным образом определить мгновенную частоту f_inst:

x(t) = A sin(phi(t))
f_inst = d/dt(phi(t)) / (2*pi)

То, что вы хотите сделать, является противоположностью этому, у вас есть заданная мгновенная частота (ваш логарифмический цикл), который вам нужно преобразовать в фазу. Поскольку противоположностью деривации является интеграция, вы можете рассчитать соответствующую фазу следующим образом (все еще формулы):

phi(t) = 2 * pi * Integral_0_to_t {f_inst(t) dt}
x(t) = A sin(phi(t))

То, что вы делаете здесь, это какая-то фазовая модуляция сигнала (с нулевой частотой) для получения необходимой мгновенной частоты. Это довольно легко сделать в NumPy:

from pylab import *
n = 1000 # number of points
f1, f2 = 10, 30 # frequency sweep range in Hertz

t = linspace(0,1,1000)
dt = t[1] - t[0] # needed for integration

# define desired logarithmic frequency sweep
f_inst = logspace(log10(f1), log10(f2), n)
phi = 2 * pi * cumsum(f_inst) * dt # integrate to get phase

# make plot
plot(t, sin(phi))
xlabel('Time (s)')
ylim([-1.2, 1.2])
grid()
show()

Результирующее изображение:

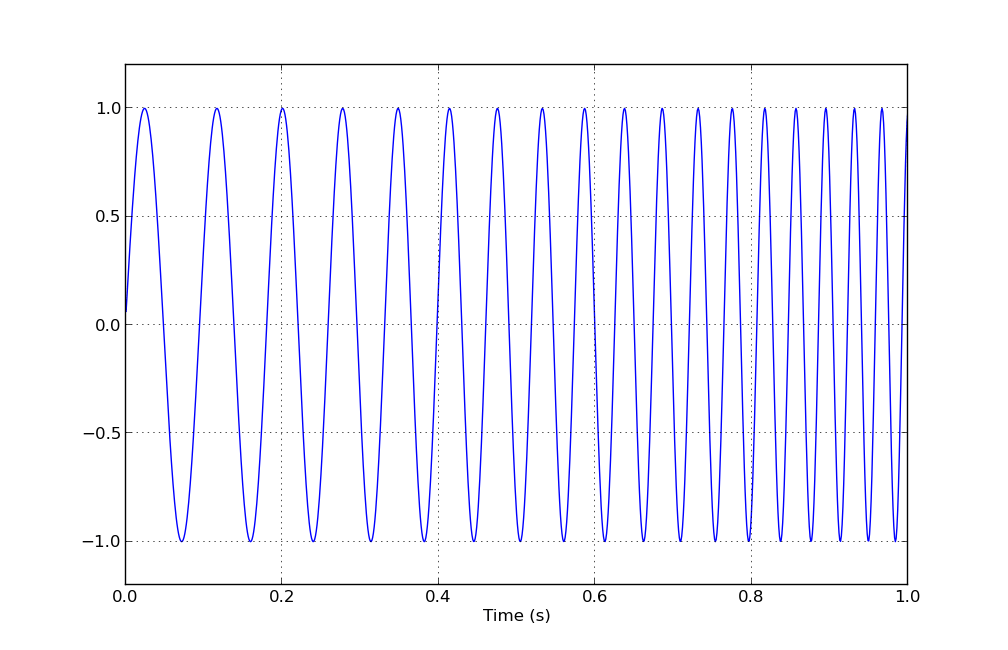
Но (как также отмечено в обмане, упомянутом Дейвом), вы, вероятно, не хотите логарифмическую развертку, а экспоненциальную. Ваше ухо имеет логарифмическое восприятие частоты, поэтому плавная / линейная музыкальная шкала (например, клавиши на фортепиано) разнесена экспоненциально. Это может быть достигнуто простым переопределением вашей мгновенной частоты f_inst(t) = f1 * exp(k * t), где k выбран так, что f_inst(t2) = f2,

Если вы хотите использовать амплитудную модуляцию одновременно, вы можете просто изменить A в зависимости от времени A(t) в формулах.

Answer 3

Этот старый вопрос попался мне на глаза, когда он появился в правом поле другого вопроса в списке связанных вопросов. Ответы Баса Суинкелса и Эндрю Кука великолепны; Я добавляю этот ответ, чтобы указать, что SciPy имеет функцию scipy.signal.chirp для генерации такого сигнала. Для экспоненциального изменения частоты используйте method="logarithmic", (Аргумент method так же может быть "linear", "quadratic" или же "hyperbolic", Для чирпа, использующего произвольный многочлен, вы можете использовать scipy.signal.sweep_poly.)

Вот как вы можете использовать chirp для генерации развертки от 1 Гц до 10 Гц в 1000 выборках в течение 5 секунд:

import numpy as np
from scipy.signal import chirp
import matplotlib.pyplot as plt

T = 5
n = 1000
t = np.linspace(0, T, n, endpoint=False)
f0 = 1
f1 = 10
y = chirp(t, f0, T, f1, method='logarithmic')

plt.plot(t, y)
plt.grid(alpha=0.25)
plt.xlabel('t (seconds)')
plt.show()