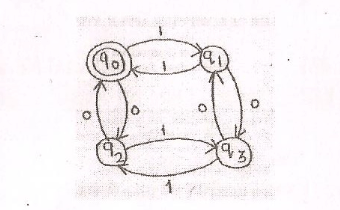
Нужно регулярное выражение для конечных автоматов: четное число 1 и четное число 0

Question

Моя проблема может звучать иначе для вас.

Я начинающий, и я изучаю конечные автоматы. Я пытаюсь найти в Интернете регулярное выражение для конечных автоматов данной машины.

Может кто-нибудь помочь мне написать "Регулярное выражение для конечных автоматов" выше машины

Любая помощь будет оценена

Answer 1

Как написать регулярное выражение для DFA, используя теорему Ардена

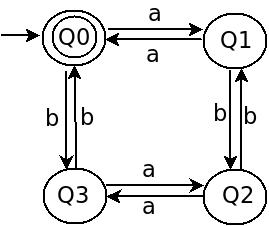
Позволяет вместо языковых символов 0, 1 мы принимаем Σ = {a, b} и следующий новый DFA.

Обратите внимание на начальное состояние Q ₀

Вы не дали, но в моем ответе начальное состояние Q ₀, где конечное состояние также Q ₀.

Язык, принятый DFA - это набор всех строк, состоящих из символа a а также b где номер символа a а также b даже (в том числе Λ).

Некоторые примеры строк {Λ, aa, bb, abba, babbab } Нет ограничений по порядку и типу появления символа, просто оба должны быть четным числом раз.
нота: Λ разрешено, потому что numberOf (a) и numberOf (b) это ноль, который является четным.

Как я уже сказал в своем выложенном ответе: Как написать регулярное выражение для DFA, в каждом штате хранится некоторая информация. Ниже приведена информация, которая хранится в каждом состоянии вышеупомянутого DFA.

Q ₀: четное число a и четное количество b
Q ₁: нечетное число a и четное количество b
Q ₂: Нечетное число a и нечетное число b
Q ₃: четное число a и нечетное число b

(Вы можете создавать DFA для более интересных языков, изменяя набор окончательных вариантов)
_{Нужно прочитать выложенный ответ, потому что мой подход к штрафу RE для DFA в обоих ответах отличается}

Что такое регулярное выражение?
Подход, описанный ниже с использованием терма Ардена, может быть применим к диаграмме переходов, в которой существует одно стартовое состояние и не определен нулевой ход (наш DFA находится в этой форме). Эту технику объясняют в книге " Формальные языки и теория автоматов".

Помните 4.2. ТЕОРЕМА АРДЕНА:

Позволять B а также C быть два регулярных выражений над Σ, Если C не содержит Λ тогда для уравнения A = B + AC существует единственное (одно и только одно) решение A = BC *.

[Решение]:

Шаг 1: Запишите исходное уравнение, одно уравнение для каждого состояния в DFA. Это уравнение означает, что состояние может быть достигнуто за один шаг

Таким образом, согласно нашему DFA возможны следующие 4 уравнения:

1. Q ₀ = Λ + Q ₁ a + Q ₃ b
2. Q ₁ = Q ₀ a + Q ₂ b
3. Q ₂ = Q ₁ b + Q ₃ a
4. Q ₃ = Q ₀ b + Q ₂ a

В уравнении (1) экстра Λ потому что Q ₀ является начальным состоянием, может быть достигнуто без какого-либо ввода (точка запуска). Поскольку Q ₀ также является только конечным состоянием, строка состоит из a, b допустимо, если оно заканчивается в Q ₀. Значение Q ₀ даст нам необходимое регулярное выражение, поэтому нашей целью является просто уравнение (1) с точки зрения a, b,

Шаг 2: Упростите уравнение, используя значение состояний из других уравнений и используя уравнение упрощения Ардена.

Давайте сначала возьмем уравнение (4) и заменим значение Q ₂ из уравнения (3).

Q ₃ = Q ₀ b + Q ₂ a
Q ₃ = Q ₀ b + (Q ₁ b + Q ₃ a) a
Q ₃ = Q ₀ b + Q ₁ ba + Q ₃ aa

Последнее уравнение можно посмотреть в виде уравнения Ардена A = B + AC, Где A является Q ₃, B = Q ₀ b + Q ₁ ba и C = aa, Таким образом, согласно терму Ардена, уравнение Q ₃ = Q ₀ b + Q ₁ ba + Q ₃ aa имеет единственное решение, которое:

Q ₃ = (Q ₀ b + Q ₁ ba) (аа) *

Или можно написать это следующим образом:

5. Q ₃ = Q ₀ b (aa) * + Q ₁ ba (aa) *

Логически вы можете проверить / понять уравнение (5), что означает, что Q ₃ может быть достигнут двумя способами (+) кулак от подачи b на Q _0, то есть цикл с меткой aa на Q ₃, второй путь от Q ₁ с применением ba,

Аналогичным образом, мы можем упростить уравнение- (2)

Q ₁ = Q ₀ a + Q ₂ b
Q ₁ = Q ₀ a + (Q ₁ b + Q ₃ a) b
Q ₁ = Q ₀ a + Q ₁ bb + Q ₃ ab

Используйте правила упрощения Ардена здесь.

Q ₁ = (Q ₀ a + Q ₃ ab) (bb) *

дальнейшее упрощение

6. Q ₁ = Q ₀ a (bb) * + Q ₃ ab (bb) *

Теперь значение Q ₃ из уравнения-(5) в уравнение-(6)

Q ₁ = Q ₀ a (bb) * + (Q ₀ b (aa) * + Q ₁ ba (aa) *) ab (bb) *
Q ₁ = Q ₀ a (bb) * + Q ₀ b (aa) * ab (bb) * + Q ₁ ba (aa) * ab (bb) *

Снова улучшите это последнее уравнение, используя закон упрощения Ардена.

Q ₁ = (Q ₀ a (bb) * + Q ₀ b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) *

возьмите Q ₀ conman:

7. Q ₁ = Q ₀ (a (bb) * + b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) *

Можете ли вы понять это уравнение, как вы можете перейти к Q ₁ из состояния Q ₀? Мы запомним это решение как уравнение (7)

Как и выше, мы можем оценить значение Q ₁ в терминах состояния Q ₀ и a, b Точно так же мы должны оценить значение для состояния Q ₃. Для этого мы можем просто положить значение состояния Q ₁ из уравнения (5) в уравнение (7).

5. Q ₃ = Q ₀ b (aa) * + Q ₁ ba (aa) *
. Q ₃ = Q ₀ b (aa) * + Q ₀ (a (bb) * + b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) * ba (aa) *
8. Q ₃ = Q ₀ (b (aa) * + (a (bb) * + b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) * ba (aa) *)

Теперь, в уравнении номер (1), положительно воспринимайте значения состояний Q ₃ и Q ₁ из чисел уравнения (8) и (7).

Q ₀ = Λ + Q ₁ a + Q ₃ b
Q ₀ = Λ + Q ₀ (a (bb) * + (aa) * ab (bb) *) (ba (aa) * ab (bb) *) * a + Q ₀ (b (aa) * + (a (bb) * + b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) * ba (aa) *) b

Теперь, в прошлый раз, примените решение Ардена, чтобы найти значение состояния Q ₀ в терминах символов. a а также b,

Q ₀ = Λ + ((a (bb) * + (aa) * ab (bb) *) (ba (aa) * ab (bb) *) * a + (b (aa) * + (a (bb) * + b (аа) * а (бб) *) (ба (аа) * аб (бб) *) * ба (аа) *) б) *

это так же, как (мы можем отказаться Λ здесь) RE:

((a (bb) * + (aa) * ab (bb) *) (ba (aa) * ab (bb) *) * a + (b (aa) * + (a (bb) * + b (aa)) * ab (bb) *) (ba (aa) * ab (bb) *) * ba (aa) *) b) *

Это то, что вы ищете.

Я не уверен, что это можно еще упростить. Я оставляю это как упражнение для вас.

В связанном вопросе я предложил неформальный и аналитический метод, но было трудно применить и найти RE для этого DFA, и этот вопрос демонстрирует силу теоремы Ардена и пошаговое решение.

Редактировать:

Мое предыдущее регулярное выражение правильное, но сложное для винограда из-за несимметричной формы. Ниже я пишу новую форму RE, которая является более симметричной.

У нас есть уравнения-(5), (6) следующим образом:

5. Q ₃ = Q ₀ b (aa) * + Q ₁ ba (aa) *
6. Q ₁ = Q ₀ a (bb) * + Q ₃ ab (bb) *

Оба симметричны по конструкции и просты в освоении. (прочитайте мой комментарий после eq-(5) выше)

Чтобы оценить значение состояния Q ₁ в терминах Q ₀, я поместил значение Q ₃ из уравнения (5) в уравнение (6), которое дает мне уравнение (7) следующим образом:

7. Q ₁ = Q ₀ (a (bb) * + b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) *

Точно так же, чтобы оценить значение состояния Q ₃ в терминах Q ₀, мы можем поместить значение Q ₁ из уравнения-(6) в уравнение-(5), которое даст нам новую форму уравнения-(8) следующим образом:

Q ₃ = Q ₀ b (aa) * + Q ₁ ba (aa) *
Q ₃ = Q ₀ b (aa) * + (Q ₀ a (bb) * + Q ₃ ab (bb) *) ba (aa) *
Q ₃ = Q ₀ b (aa) * + Q ₀ a (bb) * ba (aa) * + Q ₃ ab (bb) * ba (aa) *

Теперь мы можем получить уравнение (8) в желаемой форме:

8. Q ₃ = Q ₀ (b (aa) * + a (bb) * ba (aa) *) (ab (bb) * ba (aa) *) *

Теперь у нас есть уравнения- (1), (7), (8):

1. Q ₀ = Λ + Q ₁ a + Q ₃ b
7. Q ₁ = Q ₀ (a (bb) * + b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) *
8. Q ₃ = Q ₀ (b (aa) * + a (bb) * ba (aa) *) (ab (bb) * ba (aa) *) *

Теперь мы можем получить уравнение (8) в желаемой форме:

8. Q ₃ = Q ₀ (b (aa) * + a (bb) * ba (aa) *) (ab (bb) * ba (aa) *) *

Теперь у нас есть уравнения- (1), (7), (8):

1. Q ₀ = Λ + Q ₁ a + Q ₃ b
7. Q ₁ = Q ₀ (a (bb) * + b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) *
8. Q ₃ = Q ₀ (b (aa) * + a (bb) * ba (aa) *) (ab (bb) * ba (aa) *) *

Теперь поместите значение состояния Q ₁ и Q ₃ в уравнение- (1):

Q ₀ = Λ + Q ₀ (a (bb) * + b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) * a + Q ₀ (b (aa) * + a (bb) * ba (aa) *) (ab (bb) * ba (aa) *) * b

также может быть записано как:

Q ₀ = Λ + Q ₀ ((a (bb) * + b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) * a + (b (aa) * + a (bb) * ba (aa) *) (ab (bb) * ba (aa) *) * b)

Затем примените теорему Ардена к этому уравнению, и мы получим окончательное RE:

Регулярное выражение для четных чисел 'a' и четных чисел 'b':

((a (bb) * + b (aa) * ab (bb) *) (ba (aa) * ab (bb) *) * a + (b (aa) * + a (bb) * ba (aa) *) (ab (bb) * ba (aa) *) * b) *

Можно ли еще один шаг упростить, как показано ниже:

((a + b(aa)*ab)(bb)*(ba(aa)*ab(bb)*)*a + (b + a(bb)*ba)(aa)*(ab(bb)*ba(aa)*)*b)*

Answer 2

Пусть E - это язык с четным числом a и четным числом b, а ниже - регулярное выражение для языка E.

[00 + 11 + (01 + 10) (11 + 00)(01 + 10)]

00 = тип1

11 = тип2

(01 + 10) (00 + 11) * (01 + 10) = тип 3

Предположим, что мы сканируем слово на языке E слева направо, читая буквы по два за раз. Сначала мы приходим к двойному 0 (тип1), затем к двойному 1 (тип2), затем к другому двойному 0 (снова тип 1). Тогда, возможно, мы натолкнемся на пару букв, которые не совпадают. Скажем, например, что следующие две буквы - 10. Это должно начинать подстроку типа 3. Он начинается с не удвоенной пары (либо 01, либо 10), затем имеет раздел с удвоенными буквами (много повторений по 00 или 11), а затем, наконец, заканчивается другой удвоенной парой (опять же, либо 01 или 10). Одно свойство этого раздела слова состоит в том, что оно имеет четное число 0 и четное число 1. Если раздел начинается с 10, он может заканчиваться на 01, все еще давая два 0 и два 1 на концах только с удвоенными буквами между ними. Если бы он начинался с 10 и заканчивался 01, опять же, это дало бы четное число 0 и четное число 1. После этого раздела типа 3 мы можем продолжить работу с несколькими разделами типа или типа 2, пока не встретим еще одну недвоенную пару, начиная еще один раздел типа 3. Мы знаем, что еще одна удвоенная пара подойдет, чтобы уравновесить начальную. Общий эффект состоит в том, что каждое слово языка E содержит четное число 0 и четное число 1

Answer 3

Это DFA четно-четного языка, содержащий четные числа 0 и 1

его RE будет этим

(00 + 11 + (01+10)(01+10) (00 + 11)*)*

здесь, он будет принимать лемду, чётное число 0 и 1

или примет (00) четное число nmbr, равное 0, и 1 не означает, что здесь число nmber равно четному. Или либо (11) в этом случае число nmber равно (0), так что вы можете проверить, что он будет генерировать строки, содержащие четные число 0 и 1..

надеюсь, это решит вашу проблему