Какой язык у этих детерминированных конечных автоматов?

Дано:

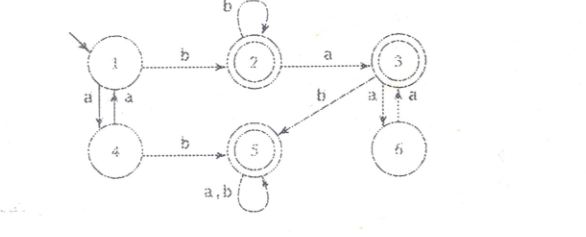
Я понятия не имею, что такое принятый язык.

Посмотрев на него, вы можете получить несколько конечных результатов:

1.) bb
2.) ab(a,b)
3.) bbab(a, b)
4.) bbaaa
Источник

3 ответа

Решение

Как написать регулярное выражение для DFA

В любом автомате назначение состояния подобно элементу памяти. Состояние хранит некоторую информацию в автоматическом режиме, например, переключатель вентилятора ON-OFF.
Детерминированные конечные автоматы (DFA) называются конечными автоматами, потому что конечный объем памяти присутствует в виде состояний. Для любого обычного языка (RL) DFA всегда возможен.

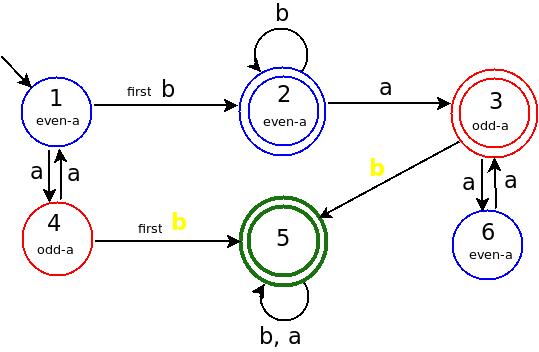
Посмотрим, какая информация хранится в DFA (см. Мою красочную фигуру).
(примечание: в моем объяснении любое число означает ноль или более раз и Λ является нулевым символом)

State-1: состояние START и информация, хранящаяся в нем, является четным числом a был пришел. И НОЛЬ b,
Регулярное выражение (RE) для этого состояния = (aa)*,

Состояние-4: Нечетное число a был пришел. И НОЛЬ b,
Регулярное выражение для этого состояния = (aa)*a,

ЦИФРА

Рисунок: ГОЛУБЫЕ состояния = ДАЖЕ число a и RED состояния = количество ODD a был пришел.

ВНИМАНИЕ: После того, как первый b пришел, движение не может вернуться в состояние 1 и состояние 4.

Состояние-5: наступает после Yellow b, Yellow b средства b after odd numbers of a,
Как только вы получаете b после нечетных чисел a (в состоянии 5) все приемлемо, потому что в состоянии 5 есть собственная петля для (b, a).

Вы можете написать для состояния-5: Yellow-b, за которым следует любая строка a, b, которая = Yellow-b(a + b)*

Состояние-6: Просто чтобы различать, странно ли a или даже.

Состояние-2: наступает даже после a затем b тогда любое количество b, знак равно (aa)*bb*

Состояние-3: идет после состояния-2, затем сначала a затем идет цикл через состояние-6. Мы можем написать для государства-3 приходит = state-2a(aa)* знак равно (aa)*bb*a(aa)*

Поскольку в нашем DFA у нас есть три конечных состояния, поэтому язык, принятый DFA, представляет собой объединение (+ в RE) из трех RL (или трех RE).
Таким образом, язык, принятый DFA, соответствует трем принимающим государствам - 2,3,5, и мы можем написать так:

 State-2 +  state-3           + state-5

(aa)*bb* + (aa)*bb*a(aa)* + Yellow-b(a + b)*

Я забыл объяснить how Yellow-b comes?
ОТВЕТ: Yellow-b это b после состояния-4 или состояния-3. И мы можем написать как:

Yellow-b знак равно ( state-4 + state-3 )b = ((aa)*a + (aa)*bb*a(aa)*) b

[ ОТВЕТ ]
(aa)*bb* + (aa)*bb*a(aa)* + ((aa)*a + (aa)*bb*a(aa)*) b(a + b)*

Английский Описание языка: DFA принимает объединение трех языков

  • ДАЖЕ ЧИСЛО a СЛЕДУЕТ ОДИН ИЛИ БОЛЬШЕ b "S,
  • ДАЖЕ ЧИСЛО a СЛЕДУЕТ ОДИН ИЛИ БОЛЬШЕ b с последующими номерами a "S.
  • Префикс строка a А ТАКЖЕ b С нечетным числом a СЛЕДУЮЩАЯ b СЛЕДУЕТ ЛЮБОЙ СТРОКОЙ a А ТАКЖЕ b А ТАКЖЕ Λ,

Английское описание является сложным, но это единственный способ описать язык. Вы можете улучшить его, сначала преобразовав данный DFA в минимизированный DFA, а затем напишите RE и описание.

Кроме того, существует производный метод для нахождения RE из заданного графа переходов с использованием терма Ардена. Я объяснил здесь, как написать регулярное выражение для DFA с использованием теоремы Ардена. Граф переходов сначала должен быть преобразован в стандартную форму, в которой нет нулевого хода и единственного начального состояния. Но мне нравится изучать теорию вычислений на основе анализа вместо математического подхода к выводу.

Источник

Я думаю, что этот вопрос больше не актуален:) и, вероятно, лучше провести вас через него, чем просто сформулировать ответ, но я думаю, что у меня есть базовое выражение, которое охватывает его (возможно, оно минимизируется), поэтому я просто напишу его вниз для будущих искателей

(aa)*b(b)* // for stoping at 2
U
(aa)*b(b)*a(aa)* // for stoping at 3
U
(aa)*b(b)*a(aa)*b((a)*(b)*)* // for stoping at 5 via 3
U
a(aa)*b((a)*(b)*)* // for stoping at 5 via 4
Источник

Примеры (1 - 4), которые вы приводите, не соответствуют языку, принятому DFA. Это просто строки, которые принадлежат языку, который принимает DFA. Поэтому все они падают на одном языке.

Если вы хотите выяснить регулярное выражение, которое определяет этот DFA, вам нужно будет сделать то, что называется индукцией k-пути, и вы можете прочитать об этом здесь.

Источник
Другие вопросы по тегам