Как установить источник для меша с помощью mplot3d?

Question

Следуя примеру в документе scikit-image, я генерирую сферическую поверхностную сетку с алгоритмом марширующих кубов. Я хочу центрировать единичную сферу оболочки в начале координат, заданном сеткой x,y,z. Однако я не могу этого сделать, так как не знаю, как поместить информацию x,y,z в mpl_toolkits.mplot3d.art3d.Poly3DCollection. Вот код:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from skimage import measure
import numpy as np

x, y, z = np.ogrid[-4:4:20j, -4:4:20j, -4:4:20j]
r = np.sqrt(x ** 2 + y ** 2 + z ** 2)
verts, faces, normals, values = measure.marching_cubes_lewiner(r,level=1)
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
mesh = Poly3DCollection(verts[faces])
mesh.set_edgecolor('k')
ax.add_collection3d(mesh)
plt.show()

Проблема в том, что marching_cubes_lewiner функция не берет x,y,z в учетную запись. Как я могу центрировать результирующую сферу в 0,0,0, как подразумевается сеткой?

Answer 1

measure.marching_cubes_lewiner берет индексы точек в сетке для расчета топологии. Кажется, что у него нет способа указать реальную сетку и никакого смещения к ней.

Следовательно, вы можете манипулировать verts по желанию. Т.е. сначала можно умножить на разницу между точками сетки, эффективно масштабируя выходные данные, а затем добавить смещение сетки. В этом случае преобразование будет newverts = 0.42105 * oldverts - 4,

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
from skimage import measure

x, y, z = np.ogrid[-4:4:20j, -4:4:20j, -4:4:20j]
r = np.sqrt(x ** 2 + y ** 2 + z ** 2)

verts, faces, normals, values = measure.marching_cubes_lewiner(r, level=1)

verts *= np.array([np.diff(ar.flat)[0] for ar in [x,y,z]])
verts += np.array([x.min(),y.min(),z.min()])

fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
mesh = Poly3DCollection(verts[faces])
mesh.set_edgecolor('k')
ax.add_collection3d(mesh)
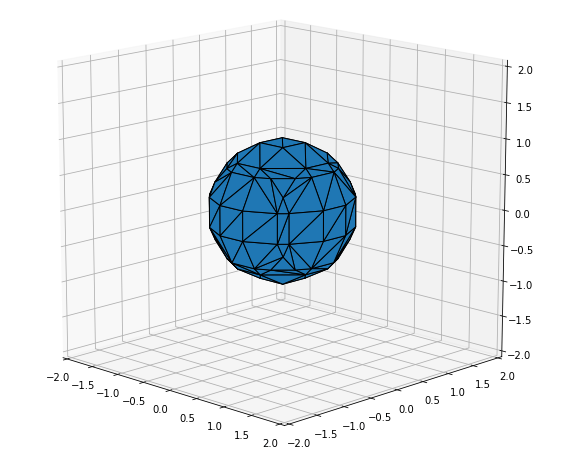
ax.set_xlim(-2, 2) 
ax.set_ylim(-2, 2)
ax.set_zlim(-2, 2)
plt.show()