Интерпретировать результаты линейной регрессии Matlab

Question

Я пытаюсь соответствовать модели, имеющей в качестве предиктора переменные TNST а также Seff и как ответ переменная AUCMET, Результат примерки:

    mdl1 = 


Linear regression model:
    AUCMET ~ 1 + TNST + Seff

Estimated Coefficients:
                   Estimate    SE         tStat      pValue    
    (Intercept)     1251.5      72.176      17.34    1.4406e-58
    TNST           -2.3058     0.16045    -14.371    1.9579e-42
    Seff            13.087      1.0748     12.176    9.4907e-32


Number of observations: 932, Error degrees of freedom: 929
Root Mean Squared Error: 322
R-squared: 0.197,  Adjusted R-Squared 0.195
F-statistic vs. constant model: 114, p-value = 5.36e-45

Результат от анова анализа

anova(mdl1)

ans = 

             SumSq         DF     MeanSq        F         pValue    
    TNST     2.1395e+07      1    2.1395e+07    206.52    1.9579e-42
    Seff     1.5359e+07      1    1.5359e+07    148.25    9.4907e-32
    Error    9.6243e+07    929     1.036e+05  

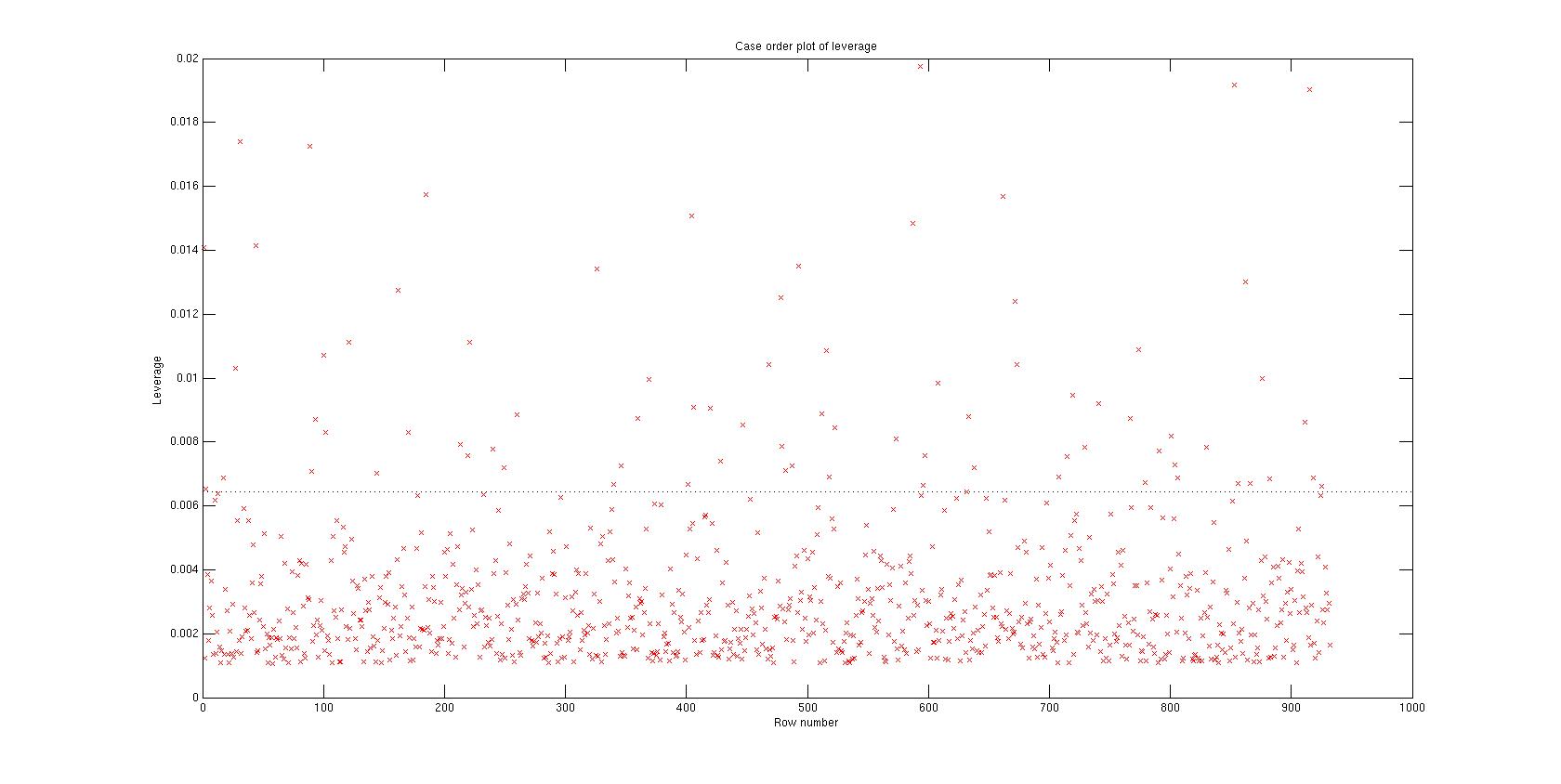
Выход диагностического участка

plotDiagnostics(mdl)

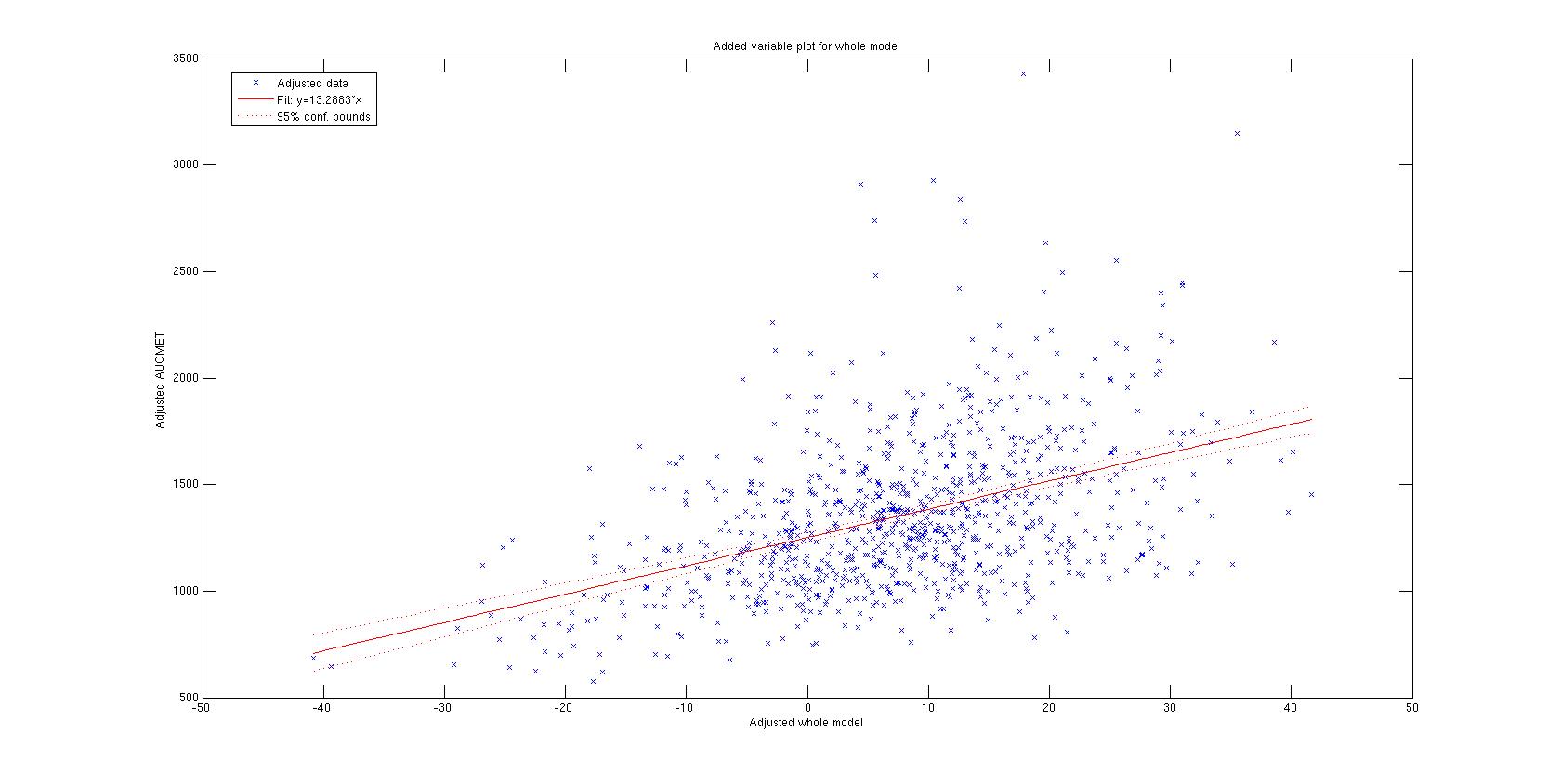
Не могли бы вы помочь мне интерпретировать этот результат? Я вижу, что все р< 0,05, поэтому они переменные важны для модели. Это хорошая модель? на что мне смотреть, чтобы понять это?

Answer 1

Изменить: Теперь, когда вы отредактировали вопрос с новой информацией:

1- Из диагностического теста на графике видно, что существует процент точек с высоким кредитным плечом. Но этот график не показывает, являются ли точки высокого левереджа выбросами. Пытаться plotDiagnostics(mdl,'cookd') чтобы найти выбросы (точки с большим расстоянием Кука) и удалить их из данных.

2- Таблица ANOVA показывает, что обе переменные важны, и вы не можете рассмотреть возможность их удаления.

---

Является ли низкий R-квадрат плохо?

Нет. В таких областях, как прогнозирование поведения человека (например, психология), значения R-квадрата низкие, потому что поведение человека трудно предсказать. Кроме того, если полученный R-квадрат низкий, но прогноз хороший, модель считается хорошей моделью. Таким образом, низкий R-квадрат не обязательно влияет на интерпретацию значимых переменных. Насколько высоким должен быть R-квадрат для предсказания? Ну, это зависит от ваших требований к ширине интервала прогнозирования и степени изменчивости ваших данных. Хотя для точных прогнозов требуется высокий R-квадрат, сам по себе этого, как мы увидим, недостаточно. С другой стороны, значения высокого R-квадрата не являются хорошими по своей сути. Высокий R-квадрат не обязательно означает, что модель хорошо подходит. ( читать дальше)

Что делать дальше?

Чтобы проверить качество модели вы можете выполнить другие тесты, такие как

1. ANOVA

Чтобы проверить качество установленной модели, обратитесь к таблице ANOVA.

tbl = anova(mdl)

2. Диагностические участки

Диагностические графики помогут вам определить выбросы и увидеть другие проблемы в вашей модели или пригонке.

plotDiagnostics(mdl)

3. Остаточные

Существует несколько остаточных графиков, которые помогут вам обнаружить ошибки, выбросы или корреляции в модели или данных. Простейшими графиками остатков являются график гистограммы по умолчанию, который показывает диапазон остатков и их частот, и график вероятностей, который показывает, как распределение остатков сравнивается с нормальным распределением с согласованной дисперсией.

plotResiduals(mdl)

4. И больше

Answer 2

R-квадрат / скорректированный r-квадрат - коэффициент корреляции Пирсона. https://en.m.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient

1 - это хорошо, а 0 - плохо, поэтому я бы сказал, что это плохая поэтическая модель.