Как рассчитать площадь 2-го многоугольника?
Предполагая ряд точек в двумерном пространстве, которые не пересекаются самостоятельно, каков эффективный метод определения площади полученного многоугольника?
Как примечание, это не домашняя работа, и я не ищу код. Я ищу описание, которое я могу использовать для реализации моего собственного метода. У меня есть свои идеи о том, чтобы вытащить последовательность треугольников из списка точек, но я знаю, что есть множество крайних случаев относительно выпуклых и вогнутых многоугольников, которые я, вероятно, не поймаю.
16 ответов
Вот стандартный метод AFAIK. В основном суммируйте перекрестные произведения вокруг каждой вершины. Гораздо проще, чем триангуляция.
Код Python, заданный полигоном, представленным в виде списка (x, y) координат вершин, неявно переходящих от последней вершины к первой:
def area(p):
return 0.5 * abs(sum(x0*y1 - x1*y0
for ((x0, y0), (x1, y1)) in segments(p)))
def segments(p):
return zip(p, p[1:] + [p[0]])
Комментарии Дэвида Лехави: Стоит упомянуть, почему этот алгоритм работает: это приложение теоремы Грина для функций −y и x; именно так, как работает планиметр. Более конкретно:
Формула выше =integral_over_perimeter(-y dx + x dy) =integral_over_area((-(-dy)/dy+dx/dx) dy dx) =2 Area
Крестовый продукт - это классика.
Если у вас есть миллионы таких вычислений, попробуйте следующую оптимизированную версию, которая требует вдвое меньше умножений:
area = 0;
for( i = 0; i < N; i += 2 )
area += x[i+1]*(y[i+2]-y[i]) + y[i+1]*(x[i]-x[i+2]);
area /= 2;
Я использую массив индексов для ясности. Более эффективно использовать указатели. Хотя хорошие компиляторы сделают это за вас.
Предполагается, что многоугольник является "замкнутым", что означает, что вы копируете первую точку как точку с индексом N. Также предполагается, что многоугольник имеет четное количество точек. Добавьте дополнительную копию первого пункта, если N не является четным.
Алгоритм получается путем развертывания и объединения двух последовательных итераций классического алгоритма кросс-произведения.
Я не очень уверен, как эти два алгоритма сравниваются в отношении числовой точности. У меня сложилось впечатление, что приведенный выше алгоритм лучше, чем классический, потому что умножение, как правило, восстанавливает потерю точности вычитания. При ограничении использования поплавков, как в случае с графическим процессором, это может иметь существенное значение.
РЕДАКТИРОВАТЬ: "Площадь треугольников и полигонов 2D и 3D" описывает еще более эффективный метод
// "close" polygon
x[N] = x[0];
x[N+1] = x[1];
y[N] = y[0];
y[N+1] = y[1];
// compute area
area = 0;
for( size_t i = 1; i <= N; ++i )
area += x[i]*( y[i+1] - y[i-1] );
area /= 2;
Эта страница показывает, что формула
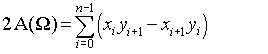
можно упростить до:

Если вы напишите несколько терминов и сгруппировать их в соответствии с общими факторами xi, равенство не трудно увидеть.
Окончательное суммирование более эффективно, так как требует только n умножения вместо 2n,
def area(x, y):
return abs(sum(x[i] * (y[i + 1] - y[i - 1]) for i in xrange(-1, len(x) - 1))) / 2.0
Я узнал об этом упрощении от Джо Кингтона, здесь.
Если у вас есть NumPy, эта версия быстрее (для всех, кроме очень маленьких массивов):
def area_np(x, y):
x = np.asanyarray(x)
y = np.asanyarray(y)
n = len(x)
shift_up = np.arange(-n+1, 1)
shift_down = np.arange(-1, n-1)
return (x * (y.take(shift_up) - y.take(shift_down))).sum() / 2.0
Набор точек без каких-либо других ограничений не обязательно однозначно определяет многоугольник.
Итак, сначала вы должны решить, какой полигон построить из этих точек - возможно, выпуклый корпус? http://en.wikipedia.org/wiki/Convex_hull
Затем триангулируйте и вычисляйте площадь. http://www.mathopenref.com/polygonirregulararea.html
Чтобы расширить области треугольника и суммировать треугольники, они работают, если у вас выпуклый многоугольник ИЛИ вам нужно выбрать точку, которая не генерирует линии для каждой другой точки, пересекающей многоугольник.
Для общего непересекающегося многоугольника необходимо суммировать перекрестное произведение векторов (контрольная точка, точка a), (контрольная точка, точка b), где a и b "соседствуют" друг с другом.
Предполагая, что у вас есть список точек, которые определяют полигон по порядку (порядок, в котором точки i и i+1 образуют линию многоугольника):
Сумма (перекрестное произведение ((точка 0, точка i), (точка 0, точка i + 1)) для i = 1 - n - 1.
Возьмите величину этого перекрестного произведения, и вы получите площадь поверхности.
Это будет обрабатывать вогнутые многоугольники, не беспокоясь о выборе хорошей контрольной точки; любые три точки, которые генерируют треугольник, который не находится внутри многоугольника, будут иметь перекрестное произведение, которое указывает в противоположном направлении любого треугольника, который находится внутри многоугольника, поэтому области суммируются правильно.
Для расчета площади многоугольника
http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=geometry1
int cross(vct a,vct b,vct c)
{
vct ab,bc;
ab=b-a;
bc=c-b;
return ab.x*bc.y-ab.y*bc.x;
}
double area(vct p[],int n)
{
int ar=0;
for(i=1;i+1<n;i++)
{
vct a=p[i]-p[0];
vct b=p[i+1]-p[0];
area+=cross(a,b);
}
return abs(area/2.0);
}
Или сделать контурный интеграл. Теорема Стокса позволяет выразить интеграл площади как контурный интеграл. Маленькая квадратура Гаусса и Боб твой дядя.
Независимое от языка решение:
ДАНА: многоугольник ВСЕГДА может быть составлен из n-2 треугольников, которые не перекрываются (n = количество точек ИЛИ сторон). 1 треугольник = 3-сторонний многоугольник = 1 треугольник; 1 квадрат = 4 односторонних многоугольника = 2 треугольника; и т.д. до тошноты QED
следовательно, многоугольник может быть уменьшен путем "отрезания" треугольников, и общая площадь будет суммой площадей этих треугольников. Попробуйте это с листом бумаги и ножницами, лучше всего, если вы сможете визуализировать процесс, прежде чем следовать.
если вы возьмете любые 3 последовательных точки в пути многоугольников и создадите треугольник с этими точками, у вас будет один и только один из трех возможных сценариев:
- Получающийся треугольник полностью внутри оригинального многоугольника
- Полученный треугольник находится полностью вне исходного многоугольника
- Полученный треугольник частично содержится в исходном многоугольнике
нас интересуют только случаи, которые попадают в первый вариант (полностью содержится).
каждый раз, когда мы находим один из них, мы отсекаем его, рассчитываем его площадь (легко, понятно, здесь не будем объяснять формулу) и создаем новый многоугольник с одной меньшей стороной (эквивалентно многоугольнику с отрезанным этим треугольником). пока у нас не осталось только одного треугольника.
как реализовать это программно:
создайте массив (последовательных) точек, которые представляют путь ВО ВРЕМЕНИ многоугольника. начать с точки 0. запустить массив, образуя треугольники (по одному за раз) из точек x, x+1 и x+2. преобразовать каждый треугольник из фигуры в область и пересечь его с областью, созданной из многоугольника. Если результирующее пересечение идентично исходному треугольнику, то указанный треугольник полностью содержится в многоугольнике и может быть отрезан. удалите x + 1 из массива и начните снова с x=0. в противном случае (если треугольник находится за пределами [частично или полностью] многоугольника), перейдите к следующей точке x + 1 в массиве.
Кроме того, если вы хотите интегрировать с картографированием и начинаете с гео-точек, вы должны сначала конвертировать из гео-точек в точки экрана. это требует принятия решения о моделировании и формуле для формы земли (хотя мы склонны думать о земле как о сфере, на самом деле это неправильный яйцевид (яйцевидная форма) с вмятинами). Есть много моделей, для получения дополнительной информации вики. Важным вопросом является то, будете ли вы считать область плоскостью или изогнутой. в общем, "маленькие" области, где точки находятся на расстоянии до нескольких километров друг от друга, не будут вызывать значительных ошибок, если рассматривать их как плоские, а не выпуклые
Внедрение формулы Shoelace можно осуществить в Numpy. Предполагая эти вершины:
import numpy as np
x = np.arange(0,1,0.001)
y = np.sqrt(1-x**2)
Мы можем определить следующую функцию, чтобы найти область:
def PolyArea(x,y):
return 0.5*np.abs(np.dot(x,np.roll(y,1))-np.dot(y,np.roll(x,1)))
И получаю результаты:
print PolyArea(x,y)
# 0.26353377782163534
Избегание петли делает эту функцию в 50 раз быстрее, чем PolygonArea:
%timeit PolyArea(x,y)
# 10000 loops, best of 3: 42 µs per loop
%timeit PolygonArea(zip(x,y))
# 100 loops, best of 3: 2.09 ms per loop
Примечание: я написал этот ответ для другого вопроса, я просто упомянул это здесь, чтобы получить полный список решений.
- Установите базовую точку (наиболее выпуклая точка). Это будет ваша точка опоры треугольников.
- Вычислите самую левую точку (произвольную), отличную от вашей базовой точки.
- Вычислите 2-ую самую левую точку, чтобы завершить ваш треугольник.
- Сохраните эту триангулированную область.
- Сдвиг на одну точку вправо на каждой итерации.
- Суммируйте триангулированные области
Один из способов сделать это - разложить многоугольник на треугольники, вычислить площадь треугольников и взять сумму за площадь многоугольника.
Лучше суммирования треугольников суммировать трапеции в декартовом пространстве:
area = 0;
for (i = 0; i < n; i++) {
i1 = (i + 1) % n;
area += (vertex[i].y + vertex[i1].y) * (vertex[i1].x - vertex[i].x) / 2.0;
}
Я хотел бы просто начать отрезать треугольники. Я не понимаю, как что-то еще могло избежать ужасно волосатых.
Возьмите три последовательных точки, которые составляют многоугольник. Убедитесь, что угол меньше 180. Теперь у вас есть новый треугольник, который не составит труда вычислить, удалите среднюю точку из списка точек многоугольника. Повторяйте, пока у вас не останется только три очка.
Я собираюсь дать несколько простых функций для расчета площади 2-го многоугольника. Это работает как для выпуклых, так и для вогнутых многоугольников. мы просто делим многоугольник на множество под-треугольников.
//don't forget to include cmath for abs function
struct Point{
double x;
double y;
}
// cross_product
double cp(Point a, Point b){ //returns cross product
return a.x*b.y-a.y*b.x;
}
double area(Point * vertices, int n){ //n is number of sides
double sum=0.0;
for(i=0; i<n; i++){
sum+=cp(vertices[i], vertices[(i+1)%n]); //%n is for last triangle
}
return abs(sum)/2.0;
}
Код Python
Как описано здесь: http://www.wikihow.com/Calculate-the-Area-of-a-Polygon
С пандами
import pandas as pd
df = pd.DataFrame({'x': [10, 20, 20, 30, 20, 10, 0], 'y': [-10, -10, -10, 0, 10, 30, 20]})
df = df.append(df.loc[0])
first_product = (df['x'].shift(1) * df['y']).fillna(0).sum()
second_product = (df['y'].shift(1) * df['x']).fillna(0).sum()
(first_product - second_product) / 2
600
C способ сделать это:
float areaForPoly(const int numVerts, const Point *verts)
{
Point v2;
float area = 0.0f;
for (int i = 0; i<numVerts; i++){
v2 = verts[(i + 1) % numVerts];
area += verts[i].x*v2.y - verts[i].y*v2.x;
}
return area / 2.0f;
}