Вейвлет-реконструкция временных рядов

Question

Я пытаюсь восстановить исходный временной ряд из вейвлет-преобразования Морлета. Я работаю в R, пакет Rwave, функция cwt. Результатом этой функции является матрица из n*m (n= период, m= время), содержащая комплексные значения.

Для восстановления сигнала я использовал формулу (11) в классическом тексте Torrence & Compo, но результат не имеет ничего общего с исходным сигналом. Я особенно обеспокоен делением между действительной частью вейвлет-преобразования и масштабом, этот шаг полностью искажает результат. С другой стороны, если я просто суммирую действительные части по всем шкалам, результат будет очень похож на исходный временной ряд, но с немного более широкими значениями (исходные ряды составляют ~ [-0,2, 0,5], а восстановленные ряды - диапазоны). ~ [-0,4,0,7]).

Мне интересно, может ли кто-нибудь рассказать о какой-то практической процедуре, формуле или алгоритме для восстановления исходного временного ряда. Я уже читал статьи Торренса и Компо (1998), Фарджа (1992) и другие книги, все с разными формулами, но мне никто не помог.

Answer 1

Я работаю над этой темой в настоящее время, используя ту же бумагу. Я покажу вам код на примере набора данных, подробно описав, как я реализовал процедуру декомпозиции и реконструкции вейвлета.

# Lets first write a function for Wavelet decomposition as in formula (1):
mo<-function(t,trans=0,omega=6,j=0){
  dial<-2*2^(j*.125)
  sqrt((1/dial))*pi^(-1/4)*exp(1i*omega*((t-trans)/dial))*exp(-((t-trans)/dial)^2/2)
}

# An example time series data: 
y<-as.numeric(LakeHuron)

Исходя из моего опыта, для правильной реконструкции вы должны сделать две вещи: сначала указать значение для получения набора данных с нулевым средним. Затем я увеличиваю максимальный масштаб. Я в основном использую 110 (хотя формула в Torrence и Compo предлагает 71)

# subtract mean from data:
y.m<-mean(y)
y.madj<-y-y.m

# increase the scale:
J<-110
wt<-matrix(rep(NA,(length(y.madj))*(J+1)),ncol=(J+1))

# Wavelet decomposition:
for(j in 0:J){
for(k in 1:length(y.madj)){
  wt[k,j+1]<-mo(t=1:(length(y.madj)),j=j,trans=k)%*%y.madj
  }
}

#Extract the real part for the reconstruction:
wt.r<-Re(wt)

# Reconstruct as in formula (11):
dial<-2*2^(0:J*.125)
rec<-rep(NA,(length(y.madj)))
for(l in 1:(length(y.madj))){
  rec[l]<-0.2144548*sum(wt.r[l,]/sqrt(dial))
}
rec<-rec+y.m

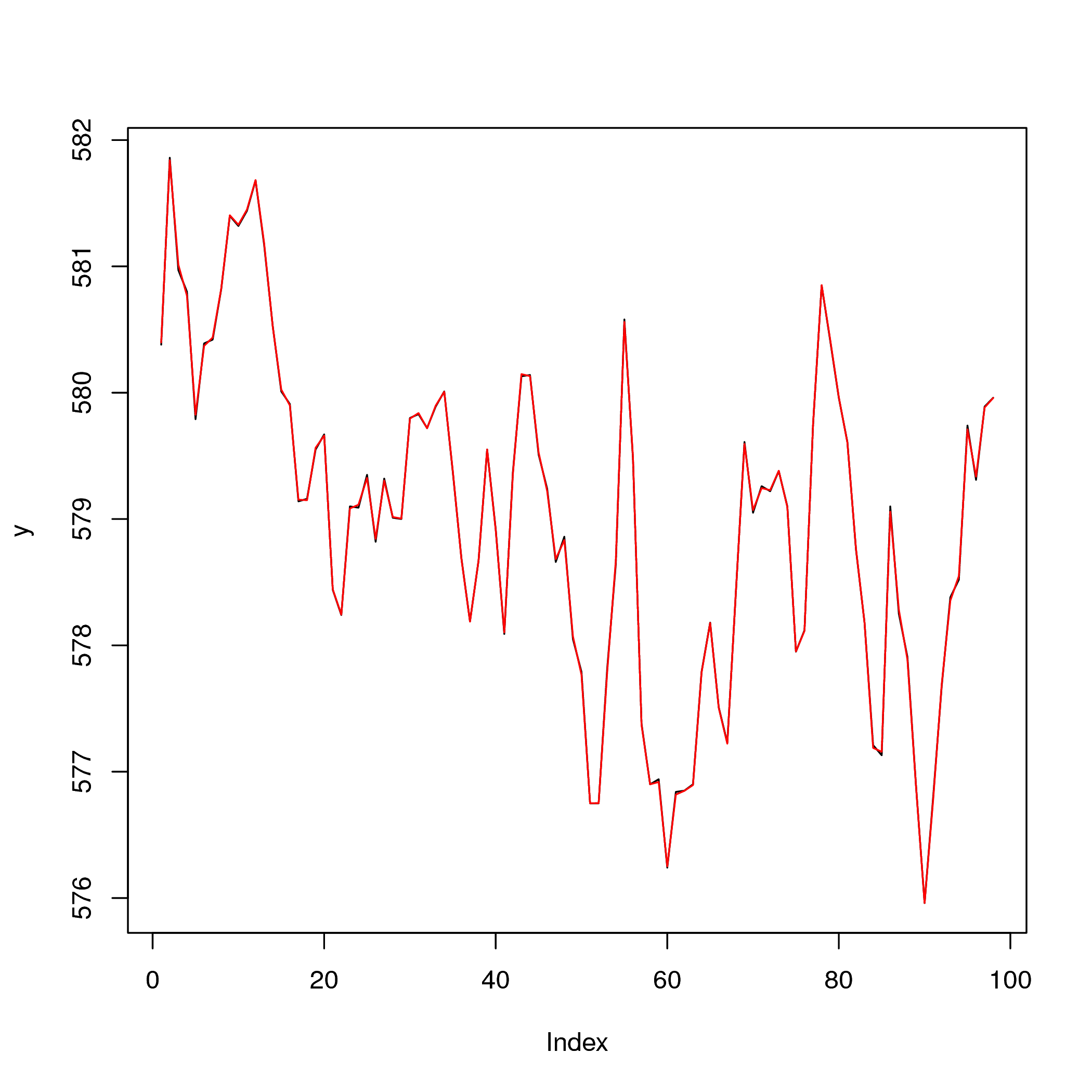
plot(y,type="l")
lines(rec,col=2)

Как вы можете видеть на сюжете, это выглядит как идеальная реконструкция: