Какая математика стоит за спрайтами 3D рекламных щитов? (было: матрица 3D преобразования в 2D матрицу)

Question

У меня есть 3D точка в пространстве. Точная ориентация / положение точки выражается через матрицу преобразования 4x4.

Я хочу нарисовать рекламный щит (3D Sprite) до этой точки. Я знаю прогнозируемое положение (то есть 3D->2D) точки; рекламный щит стоит перед камерой, так что это тоже очень полезно. Чего я не знаю, так это масштабирования, который должен иметь рекламный щит!

Чтобы сделать вещи более сложными, матрица 4x4 может иметь все виды преобразований: 3D-вращение, 3D-масштабирование, 3D-транспонирование. Предположим, что камера настолько проста, насколько это возможно: положение в (0,0,0), без вращения.

Итак, могу ли я "извлечь" масштабирование рекламного спрайта из этой матрицы 4x4?

-

БЫЛО:

У меня 3D аффинное преобразование матрицы 4х4. Мне нужно преобразовать его (проект) в 2D-матрицу аффинного преобразования 3х3, которая выглядит следующим образом:

3D повороты не имеют значения и могут быть отброшены, если они есть; Меня интересует только перевод и самое главное масштабирование.

Может ли кто-нибудь помочь с уравнениями для каждого из шести значений4? (допустим, t_x, t_y также известны)

Дополнительная информация:

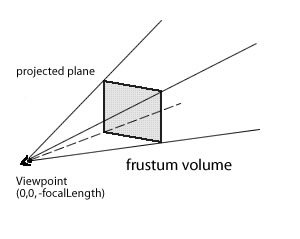
Matrix3D - это глобальное преобразование трехмерной точки, скажем, (0,0,0). Его цель - проецироваться на двухмерную плоскость (экран компьютера).

Я знаю, как проецировать 3D-точку в 2D-пространство, и мне нужно сохранить дополнительную информацию о преобразовании за пределами позиции, то есть масштабирование: как вы, возможно, знаете, свойство масштабирования также изменяется при проецировании точки на 2D-плоскость.

Я также забыл упомянуть, что свойства проекции перспективы также известны, а именно:

field of view (single value)
focal length (single value)
projection center (viewpoint position - 2D value)

Answer 1

Если вы не используете сферическую систему координат, то эта задача не может быть решена, поскольку отбрасывание Z-координаты перед проекцией приведет к удалению расстояния от точки проекции и, следовательно, вы не знаете, как применить перспективу.

У вас есть два варианта (если я что-то упустил):

1. применить матрицу трехмерного преобразования

   а затем использовать только x,y - координаты результата

2. создать матрицу преобразования 3х3 для поворота / проекции

   и добавить вектор смещения до или после его применения. Имейте в виду, что этот подход не использует однородные координаты!!!

[Edit1] уравнения для ясности

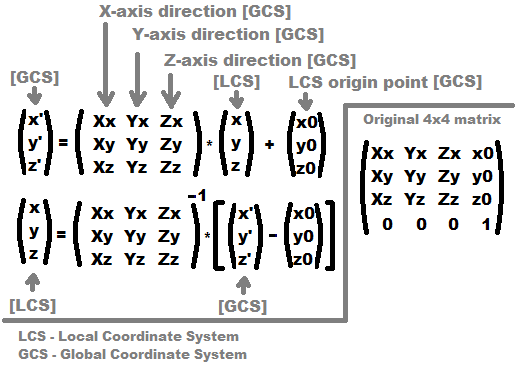
Не забудь этого 3x3 матричные + векторные преобразования не суммируются!!! Вот почему 4x4 вместо этого используются преобразования Теперь вы можете выбросить последний ряд матрицы / вектора (Xz,Yz,Zz), (z0) а затем выходной вектор просто (x', y'), Конечно, после этого вы не можете использовать обратное преобразование, потому что вы потеряли координату Z.

Масштабирование выполняется путем изменения размера векторов направления оси

Btw. если ваша проекционная плоскость также XY Самолет без поворотов тогда:

x' = (x-x0)*d/(z-z0)
y' = (y-y0)*d/(z-z0)

(x,y,z) - указать на проект
(x',y') - прогнозируемая точка
(x0,y0,z0) - происхождение проекции
d - фокусное расстояние

[Edit2] хорошо после вопроса редактировать значение совершенно другое

Я предполагаю, что вы хотите, чтобы спрайт всегда был перед камерой. Это некрасиво, но упрощает такие вещи, как трава, деревья,...

M - ваша матрица
P - матрица проекции внутри M
Если у вас есть происхождение M = (0,0,0) без поворотов / масштабирования / перекоса M=P
pnt - точка вашего рекламного щита (в центре я предполагаю) (w=1) [GCS]
dx,dy - половинный размер рекламного щита [LCS]
A,B,C,D - проецируемые края вашего рекламного щита [GCS]
[GCS] - глобальная система координат
[LCS] - локальная система координат

1. если вы знаете матрицу проекции

   Я предполагаю, что это glFrustrum или gluPerspective ... тогда:

   (x,y,z,w)=(M*(P^-1))*pnt  // transformed center of billboard without projection
   A=P*(x-dx,y-dy,z,w)
   B=P*(x-dx,y+dy,z,w)
   C=P*(x+dx,y+dy,z,w)
   D=P*(x+dx,y-dy,z,w)
   

2. Если твой M матрица слишком сложна для работы #1

   MM=(M*(P^-1))     // transform matrix without projection
   XX=MM(Xx,Xy,Xz)   // X - axis vector from MM [GCS](look at the image above on the right for positions inside matrix)
   YY=MM(Yx,Yy,Yz)   // Y - axis vector from MM [GCS]
   X =(M^-1)*XX*dx   // X - axis vector from MM [LCS] scaled to dx
   Y =(M^-1)*YY*dy   // Y - axis vector from MM [LCS] scaled to dy
   A = M*(pnt-X-Y)
   B = M*(pnt-X+Y)
   C = M*(pnt+X+Y)
   D = M*(pnt+X-Y)
   

[Edit3] только вычитание

MM=(M*(P^-1))      // transform matrix without projection
sx=|MM(Xx,Xy,Xz)|  // size of X - axis vector from MM [GCS] = scale x
sy=|MM(Yx,Yy,Yz)|  // size of Y - axis vector from MM [GCS] = scale y

Answer 2

Матрица шкалы S выглядит так:

sx 0  0  0
0  sy 0  0
0  0  sz 0
0  0  0  1

Матрица перевода T выглядит так:

1  0  0  0
0  1  0  0
0  0  1  0
tx ty tz 1

Матрица вращения оси Z Rвыглядит так:

 cos(a) sin(a)  0  0
-sin(a) cos(a)  0  0
   0      0     1  0
   0      0     0  1

Если у вас есть матрица преобразования M, это является результатом ряда умножений R, T а также S матрицы. Смотря на Mпорядок и количество этих умножений неизвестны. Однако, если мы предположим, что M=S*R*T мы можем разложить его на отдельные матрицы. Во-первых, давайте посчитаем S*R*T:

        ( sx*cos(a) sx*sin(a) 0  0)       (m11 m12 m13 m14)
S*R*T = (-sy*sin(a) sy*cos(a) 0  0) = M = (m21 m22 m23 m24)
        (     0         0     sz 0)       (m31 m32 m33 m34)
        (     tx        ty    tz 1)       (m41 m42 m43 m44)

Поскольку мы знаем, что это двумерное преобразование, получить перевод очень просто:

translation = vector2D(tx, ty) = vector2D(m41, m42)

Чтобы вычислить вращение и масштаб, мы можем использовать sin(a)^2+cos(a)^2=1:

(m11 / sx)^2 + (m12 / sx)^2 = 1
(m21 / sy)^2 + (m22 / sy)^2 = 1

m11^2 + m12^2 = sx^2
m21^2 + m22^2 = sy^2

sx = sqrt(m11^2 + m12^2)
sy = sqrt(m21^2 + m22^2)

scale = vector2D(sx, sy)

rotation_angle = atan2(sx*m22, sy*m12)

Источник

Надеюсь, это поможет вам