Подпишите результаты fft
Я пытаюсь рассчитать MTF из контрольной цели. Я легко вычисляю функцию спреда, но результаты FFT мне не совсем понятны. Подводя итог, можно сказать, что значения чередуются, давая мне отражение того, что я ожидал. Чтобы проверить, я использовал простую прямоугольную волну и numpy:
from numpy import fft
data = []
for x in range (0, 20):
data.append(0)
data[9] = 10
data[10] = 10
data[11] = 10
dataFFT = fft.fft(data)
Результаты выглядят корректно, за исключением знака... Я вижу следующее для первых 4 значений в качестве примера:
30,00000000 +0,00000000e + 00j
-29.02113033 + 7.10542736e-15j
26.18033989 -1.24344979e-14j
-21.75570505 + 1.24344979e-14j
Итак, мой вопрос, почему положительный-> отрицательный-> положительный-> отрицательный в реальной плоскости? Это не то, что я ожидал бы... Это я изобразил, почти кажется, что правильная функция отражена вокруг оси x.
Примечание: я ожидал следующее в качестве примера: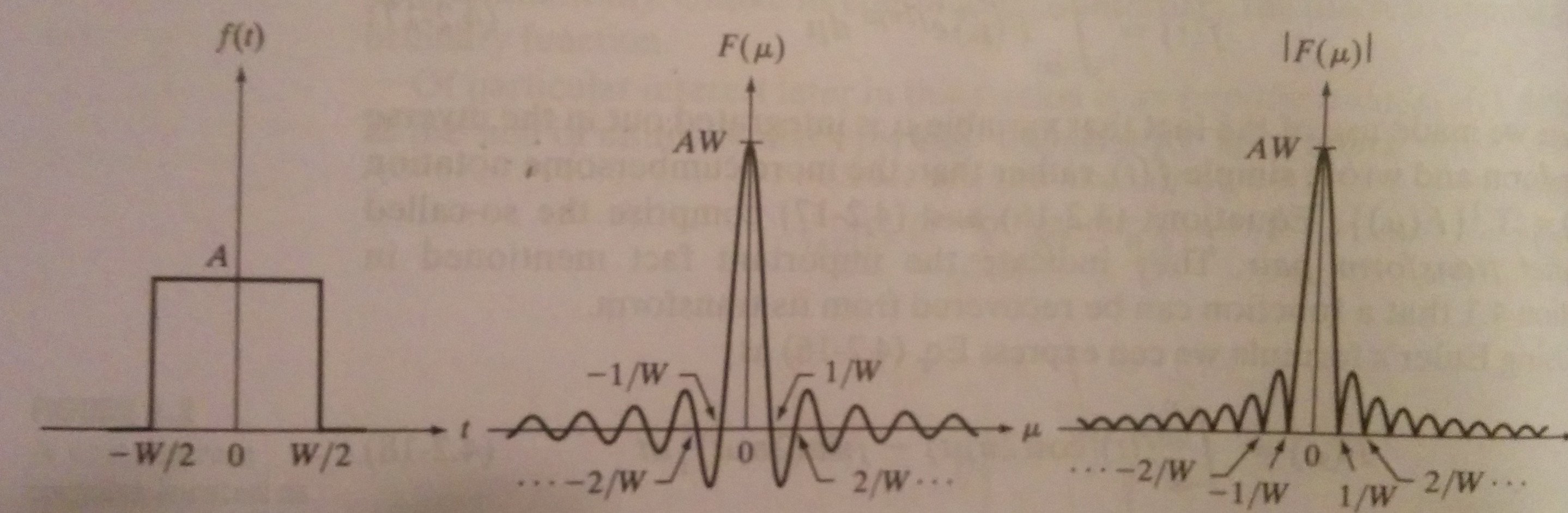
Вот что я получаю: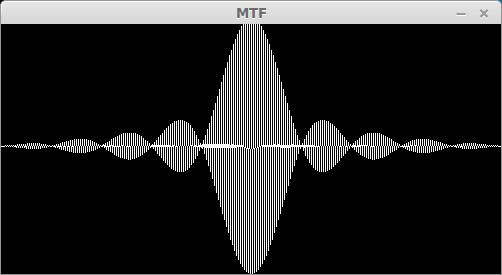
3 ответа
Ваш пульс симметричен и расположен в центре вашего окна FFT (около N/2). Симметричные реальные данные соответствуют только косинусу или "реальным" компонентам результата БПФ. Обратите внимание, что функция косинуса чередуется между -1 и 1 в центре окна БПФ, в зависимости от индекса приемника частоты (представляющего периоды косинуса на ширину БПФ). Таким образом, корреляция этих базисных функций БПФ с положительным идущим импульсом также будет чередоваться до тех пор, пока импульс находится в половине периода косинуса.
Если вы хотите, чтобы самые большие коэффициенты БПФ были в основном положительными, попробуйте центрировать свой узкий прямоугольный импульс вокруг времени 0 (или циклически, времени N), где функция косинуса всегда равна 1 для любой частоты.
Это работает, если вы перемещаете данные вокруг 0 вместо половины вашего массива с помощью:
dataFFT = fft.fft(np.fftshift(data))
вы забыли указать, являются ли ваши данные реальными или сложными
не каждый код на python/numpy (включая меня), и если вы не знаете этого, вы, вероятно, неправильно обрабатываете данные в / из FFT.
- Вход БПФ может быть как действительным, так и сложным
- БПФ выход является сложной областью
поэтому проверьте документы для вашей реализации FFT и укажите ее, а также исправьте вашу обработку данных соответствующим образом. Сложный домен обычно имеет первое значение Re и второе Im, но это зависит от реализации / конфигурации FFT.
сигнал
вот пример импульсного отклика от БПФ
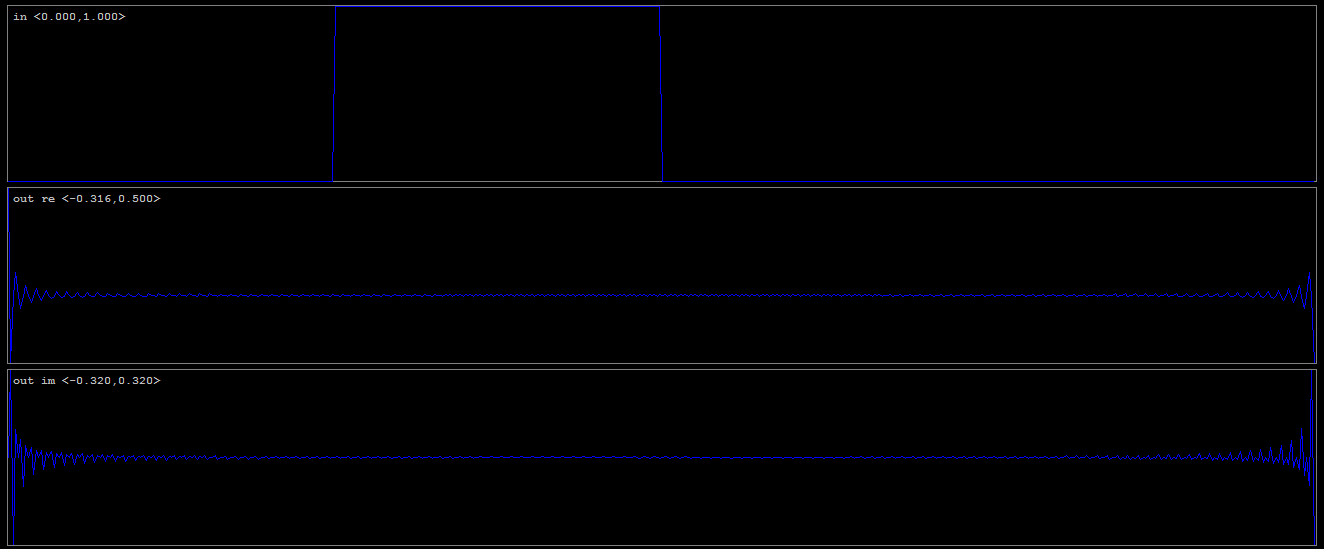 первым является входной сигнал реального домена (Im=0) одного импульса конечной ненулевой ширины, а вторым является Re- часть выходного сигнала БПФ. Третий - часть Im вывода FFT. Если вы немного увеличите масштаб, вы увидите диапазон амплитуд оси Y каждого сигнала (слева).
первым является входной сигнал реального домена (Im=0) одного импульса конечной ненулевой ширины, а вторым является Re- часть выходного сигнала БПФ. Третий - часть Im вывода FFT. Если вы немного увеличите масштаб, вы увидите диапазон амплитуд оси Y каждого сигнала (слева).Не забывайте, что разные реализации FFT могут иметь разные константы нормализации, которые изменят амплитуду сигнала. Если вы хотите, чтобы амплитуда и фаза конвертировались так:
mag=sqrt(Re*Re+Im*Im); // power ang=atanxy(Re,Im); // phase angleatanxy(dx,dy)это 4 квадрантarctanтакже называемыйatan2но будьте осторожны, чтобы получить порядок операндов так же, как вашatanxy/atan2реализация потребностей. Также можно использовать мою реализацию C++ atanxy
[Заметки]
если ваш входной сигнал - реальный домен, то выход FFT симметричен Сигналы Re и Im будут такими:
{ a0,a1,a2,a3,...,a(n-1),a(n-1)...,a3,a2,a1,a0 }
точно так же как на изображении выше. Слева низкие частоты, а в середине верхняя частота. Если ваш входной сигнал сложный домен, то на выходе может быть что угодно.
Это не все так неожиданно. Если вы хотите сравнить с обычными графиками, убедитесь, что вы конвертируете эту информацию в величину и фазу, прежде чем делать какие-либо выводы.
Я сделал быструю проверку, используя ваш код и numpy.abs для mag, numpy, angle for phase. Для меня это выглядит как функция sinc(), чего и следовало ожидать, если бы во временной области был квадратный импульс. Если вы сделаете это, вы найдете довольно широкий синус, как это было бы возможно для короткого импульса на очень небольшом количестве выборок.