Стандартные ошибки для дифференциальной эволюции

Question

Можно ли рассчитать стандартные ошибки для дифференциальной эволюции?

Из записи Википедии:

http://en.wikipedia.org/wiki/Differential_evolution

Это не на основе производных (на самом деле это одна из его сильных сторон), но как же тогда вычислить стандартные ошибки?

Я мог бы подумать, что какая-то стратегия начальной загрузки могла бы быть применимой, но не могу найти какие-либо источники, чем применить начальную загрузку к DE?

Baz

Answer 1

Что касается стандартных ошибок, дифференциальная эволюция, как и любой другой эволюционный алгоритм.

Использование стратегии начальной загрузки кажется хорошей идеей: обычные формулы предполагают нормальное (гауссовское) распределение базовых данных. Это почти никогда не относится к эволюционным вычислениям (экспоненциальные распределения встречаются гораздо чаще, вероятно, за ними следуют бимодальные распределения).

Простейший метод начальной загрузки включает взятие исходного набора данных из N чисел и выборку из него для формирования новой выборки (повторной выборки), также имеющей размер N. Повторная выборка берется из оригинала с использованием выборки с заменой. Этот процесс повторяется большое количество раз (обычно 1000 или 10000 раз), и для каждой из этих выборок начальной загрузки мы вычисляем его среднее значение / медиану (каждая из них называется оценкой начальной загрузки).

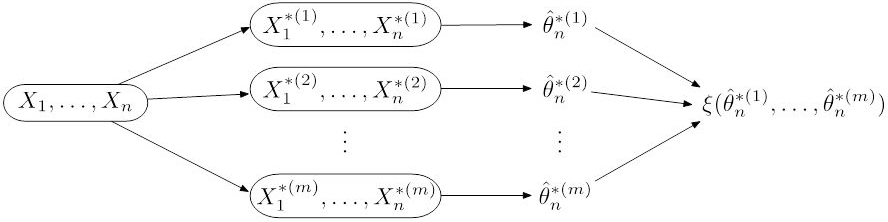
Стандартное отклонение (SD) средних значений - это стандартная ошибка начальной загрузки (SE) среднего значения, а SD медиан - это SE начального значения медианы (2,5-й и 97,5- й процентили средних значений - это 95-процентная достоверность начальной загрузки). пределы для среднего).

Предупреждения:

• слово " население" используется в разных контекстах с разными значениями (самозагрузка против эволюционного алгоритма)
• в любом ГА или ВП средняя часть населения почти ничего вам не говорит. Используйте среднее / медиану лучших
• среднее из набора, который обычно не распределяется, создает значение, которое ведет себя не интуитивно. Особенно, если распределение вероятности искажено: большие значения в "хвосте" могут доминировать, а среднее значение имеет тенденцию отражать типичное значение "худших" данных, а не типичное значение данных в целом. В этом случае лучше медиана

Некоторые интересные ссылки:

• Краткое руководство по использованию статистики в эволюционных вычислениях
• Введение в статистику для экспериментального анализа ЕС